
지난 포스트에선 활성화 함수에서 자주 사용되는 시그모이드 함수(Sigmoid Function)에 대해 학습해 보았다. 시그모이드 함수는 이진 분류에서 주로 사용되며, 보통 출력층에서만 사용된다. 은닉층에서 소프트맥스 함수가 사용되는 경우, 이전 포스트에서도 말했듯, 기울기 소실 문제 등 기울기를 제대로 찾지 못해, 학습 효율성이 감소한다는 단점이 있다.
이번 포스트에서는 이전에 학습했던 이진 분류 활성화 함수인 시그모이드가 아닌 다중 분류에 주로 사용되는 활성화 함수인 소프트맥스(Softmax) 활성화 함수에 대해 살펴보도록 하겠다.
소프트맥스 함수(Softmax Function)
- 소프트맥스는 세 개 이상으로 분류하는 다중 클래스 분류에서 사용되는 활성화 함수다.
- 소프트맥스 함수는 분류될 클래스가 n개라 할 때, n차원의 벡터를 입력받아, 각 클래스에 속할 확률을 추정한다.
1. 소프트맥스 함수 공식
$$ y_k = \frac{e^{a_k}}{\sum_{i=1}^{n}e^{a_i}} $$
- $n$ = 출력층의 뉴런 수(총 클래스의 수), $k$ = $k$번째 클래스
- 만약, 총 클래스의 수가 3개라고 한다면 다음과 같은 결과가 나오게 된다.
$$softmax(z) = [\frac{e^{z_1}}{e^{z_1}+e^{z_2}+e^{z_3}},\ \ \ \frac{e^{z_2}}{e^{z_1}+e^{z_2}+e^{z_3}},\ \ \ \frac{e^{z_3}}{e^{z_1}+e^{z_2}+e^{z_3}}] = [p_1, p_2, p_3]$$
- 위 공식을 보면, 소프트맥스 함수의 생김세는 "k번일 확률 / 전체 확률"로 꽤나 단순하다는 것을 알 수 있다.
2. 소프트맥스 함수에서 $e^x$를 사용하여, 확률을 계산하는 이유
위 소프트맥스 함수의 공식을 보면, 각 클래스에 속할 확률을 구하는 것은 알겠는데, 대체 왜 자연로그의 밑인 상수 e에 대한 지수함수를 사용하여 확률을 나타내는 것일까?
이는 소프트맥스 함수는 시그모이드 함수로부터 유도된 것이기 때문이다.
- 시그모이드 함수를 $S$라고 가정하고 $e^{f(x)}$에 대한 공식으로 변환해보자.
$$S = \frac{1}{e^{-t}+1}, \ \ \ \frac{S}{1-S} = e^{t}$$
- $\frac{S}{1-S}$에서 $S$는 "전체에서 $S$할 확률"이고 $1-S$는 "전체에서 $1-S$할 확률"이다. 즉, 앞서 봤던 오즈와 같다. 이 식은 각 집단이 독립이라는 가정하에 다음과 같이 변화시킬 수 있다.
$$ \frac{P(C_1)}{P(C_2)} = \frac{\frac{P(C_1)*P(X)}{P(X)}}{\frac{P(C_2)*P(X)}{P(X)}} = \frac{P(C_1|X)}{P(C_2|X)} = e^t$$
- 위 식은 클래스가 2개일 때의 확률을 이야기하는 것이다. 그렇다면 클래스가 K개라면 어떨까?
$$ \frac{P(C_i|X)}{P(C_K|X)} = e^{t_i} $$
- 이 식에 대하여 양변을 i = 1 부터 i = K-1까지 더해보자.
$$\sum_{i=1}^{K-1}\frac{P(C_i|X)}{P(C_K|X)} = \frac{1}{P(C_K|X)}\sum_{i=1}^{K-1}P(C_i|X) = \sum_{i=1}^{K-1}e^{t_i} $$
- 위 식에서 일부분을 이렇게 바꿀 수 있다.
$$ \sum_{i=1}^{K-1}P(C_i|X) = 1-P(C_K|X) $$
- 이를 식에 반영해보면 이렇게 된다.
$$ \frac{1-P(C_K|X)}{P(C_K|X)} = \sum_{i=1}^{K-1}e^{t_i}, \ \ \ \frac{P(C_K|X)}{1-P(C_K|X)} = \frac{1}{\sum_{i=1}^{K-1}e^{t_i}} $$
$$ P(C_K|X)\sum_{i=1}^{K-1}e^{t_i}= 1-P(C_K|X), \ \ \ P(C_K|X)(\sum_{i=1}^{K-1}e^{t_i} + 1) = 1 $$
$$ P(C_K|X) = \frac{1}{\sum_{i=1}^{K-1}e^{t_i} + 1} $$
- 위 식을 통해서 $P(C_K|X)$를 유도하였으며, 이제 처음에 만들었던 식을 이용해서 P(C_i|X)를 유도해보자.
$$ \frac{P(C_i|X)}{P(C_K|X)} = e^{t_i}, \ \ \ P(C_i|X) = e^{t_i}P(C_K|X) = \frac{e^{t_i}}{\sum_{i=1}^{K-1}e^{t_i} + 1} $$
- 분모에 있는 1은 다음과 같은 방법으로 제거한다.
$$ \frac{P(C_i|X)}{P(C_K|X)} = e^{t_i} $$
- $i = K$ 이라면
$$ \frac{P(C_K|X)}{P(C_K|X)} = 1 = e^{t_K} $$
- 위 식을 분모의 1에 넣어주자.
$$ P(C_i|X) = \frac{e^{t_i}}{\sum_{i=1}^{K-1}e^{t_i} + e^{t_K}} = \frac{e^{t_i}}{\sum_{i=1}^{K}e^{t_i}} $$
- 시그모이드에서부터 지금까지의 과정을 보면, "로짓(Logit) > 시그모이드 함수 > 소프트맥스 함수" 순으로 유도되는 것을 알 수 있다.
- 애초에 분류라는 것은 로지스틱 회귀 모델에 의해 파생되는 것이므로, 기계 학습에 대해 자세히 알기 위해선 로지스틱 회귀 모델에 대해 자세히 알 필요가 있다.
3. 소프트맥스 함수에서 $e^x$를 사용하여 얻어지는 장점
- 지수함수 단조 증가함수(계속 증가하는 함수)이기 때문에 소프트맥스에 들어가는 인자들의 대소 관계는 변하지 않는다.
- 지수함수를 적용하면, 아무리 작은 값의 차이라도 확실히 구별될 정도로 커진다.
- $e^x$의 미분은 원래 값과 동일하기 때문에, 미분을 하기 좋다.
$$\frac{d}{dx}e^x = e^x $$
# 가볍게 지수함수를 그려보자
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-5, 5, 0.1)
y = np.exp(x)
# 캔버스 설정
fig = plt.figure(figsize=(8,6)) # 캔버스 생성
fig.set_facecolor('white') # 캔버스 색상 설정
plt.plot(x, y)
plt.title("Exponential Function", fontsize = 25)
plt.xlabel('x', fontsize = 15)
plt.ylabel('y', fontsize = 15, rotation = 0)
plt.show()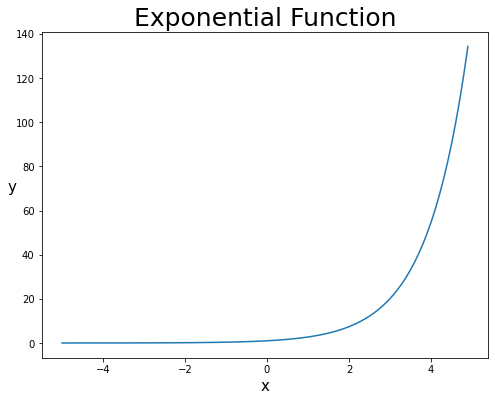
4. 소프트맥스 함수의 구현
- 위 공식을 그대로 구현해보면 다음 코드와 같다.
# 소프트맥스
>>> def softmax(x):
>>> exp_x = np.exp(x)
>>> result = exp_x / np.sum(exp_x)
>>> return result- 그러나 위 코드에는 상상치 못한 문제점이 하나 숨어있다.
- 그것은 바로, 코드 내에 지수함수가 포함되어 있다는 것인데, 지수함수는 값을 더욱 확대한다는 특징을 가지고 있으며, 만약 지나치게 큰 값이 원소로 들어가게 된다면, 값이 너무 커서 연산이 되지 않는 오버플로 문제를 일으킬 위험이 있다.
- 지수함수의 문제가 어떠한지 보기 위해 아래 코드를 보자.
>>> print(np.exp(10))
>>> print(np.exp(100))
>>> print(np.exp(1000))
22026.465794806718
2.6881171418161356e+43
inf
<ipython-input-15-2a14d587d35d>:3: RuntimeWarning: overflow encountered in exp
print(np.exp(1000))- 여기서 np.exp(x)는 $e^x$를 의미하는 함수이다.
- 고작 $e^1000$만 했을 뿐인데, 값이 무한대로 나와, RuntimeWarning이 뜨는 것을 볼 수 있다.
- 이는 softmax에 들어가는 원소들에 대하여, 그 원소들의 최댓값을 빼는 것으로 쉽게 해결할 수 있다.
>>> def softmax(x):
>>> """ 소프트맥스 함수
>>> Input: array
>>> Output: array
>>> """
>>> # Input 값에 Input 값의 최댓값을 뺀다.
>>> array_x = x - np.max(x)
>>> exp_x = np.(array_x)
>>> result = exp_x / np.sum(exp_x)
>>> return result- 위 방법이 가능한 것을 증명해보면 다음과 같다.
$$ y_k = \frac{e^{a_k}}{\sum_{i=1}^{n}e^{a_i}} = \frac{Ce^{a_k}}{C\sum_{i=1}^{n}e^{a_i}} = \frac{e^{a_k + lnC}}{\sum_{i=1}^{n}e^{a_i + lnC}} = \frac{e^{a_k + C'}}{C\sum_{i=1}^{n}e^{a_i + C'}} $$
- 위 코드를 보면 """ 주석 """를 만들어주었으며, Input, Output을 써주었다. 보다 자세히 코드에 대한 설명을 써주면 좋지만, 최소한 Input, Output되는 Data가 어떠한 형태인지는 써줄 필요가 있다.
- 위 함수에 값을 넣어 그 효과와 형태를 보자.
# 소프트맥스 함수에 임의의 값을 넣어보자
>>> x = np.array([15, 10, 20, 30, 60])
>>> softmax(x)
array([2.86251858e-20, 1.92874985e-22, 4.24835426e-18, 9.35762297e-14,
1.00000000e+00])- 가장 끝에 있는 5번째 값이 가장 크게 나오는 것을 볼 수 있다.
- 이를 그래프로 그려보자.
# 소프트맥스 함수로 그래프를 그려보자.
>>> x = np.arange(-5.0, 5.0, 0.1)
>>> y = softmax(x)
>>> fig = plt.figure(figsize=(10,7)) # 캔버스 생성
>>> fig.set_facecolor('white') # 캔버스 색상 설정
>>> plt.plot(x, y)
>>> plt.ylim(0, 0.1)
>>> plt.title("Softmax", fontsize=30)
>>> plt.xlabel('x', fontsize=20)
>>> plt.ylabel('y', fontsize=20, rotation=0)
>>> plt.show()
소프트맥스 함수는 시그모이드 함수처럼 출력층에서 주로 사용되며, 이진 분류에서만 사용되는 시그모이드 함수와 달리 다중 분류에서 주로 사용된다.
무엇보다도 소프트맥스 함수의 큰 장점은 확률의 총합이 1이므로, 어떤 분류에 속할 확률이 가장 높을지를 쉽게 인지할 수 있다.
다음 포스트에서는 시그모이드 함수의 대체제로 사용되는 활성화 함수인 하이퍼볼릭 탄젠트 함수(tanh)에 대해 학습해 보겠다.
'Machine Learning > Deep Learning' 카테고리의 다른 글
| 딥러닝-3.4. 활성화함수(5)-렐루 함수(ReLU) (0) | 2021.01.27 |
|---|---|
| 딥러닝-3.3. 활성화함수(4)-하이퍼볼릭 탄젠트 함수(tanh) (0) | 2021.01.26 |
| 딥러닝-3.1. 활성화함수(2)-시그모이드 함수(Sigmoid) (3) | 2021.01.25 |
| 딥러닝-3.0. 활성화함수(1)-계단함수와 선형함수 (4) | 2021.01.25 |
| 딥러닝-2.1. 퍼셉트론(2)-XOR 게이트 (0) | 2021.01.24 |