대푯값(Representative value)과 비대칭도(Skewness)
앞서 학습였던, 중앙값(Median), 최빈값(Mode), 평균(Mean) 등과 같은 대푯값과 표준편차(Standard Deviation)를 사용하면, 데이터가 대략 어떻게 생겼는지를 파악할 수 있다.
이번 포스트에서는 대푯값이 무엇인지, 대푯값을 사용하여 어떻게 데이터의 형태를 파악할 수 있는지에 대해 알아보도록 하자.
1. 대푯값(Representative value)
- 대푯값은 말 그대로 어떠한 데이터를 단 하나의 값으로 표현할 수 있는 값을 말한다.
- 데이터 어디에 모여있는지(중심경향치): 평균(Mean), 중앙값(Median), 최빈값(Mode), 절사 평균(Trimmed mean)
- 데이터를 정렬하고 일정 크기로 나눴을 때의 간격 점: 사분위수(Quartile), 백분위수(Percentile)
- 정상 범위에서 벗어난 값: 이상값(Outlier)
- 확률상 기대되는 대푯값: 기댓값(Expected value)
1.1. 대푯값을 이용하여, 데이터의 대략적인 분포를 알 수 있다.
- 산포도는 대푯값이 아니지만, 대푯값을 이용해서 산포도를 알 수도 있다.
- 사분위수를 이용하면, 사분위 범위를 알 수 있고, 사분위 범위를 알면, 상자 수염 그림(Box-and-Whisker plot)을 그릴 수 있다.
- 평균과 중앙값, 최빈값을 이용하여, 데이터의 대략적인 개형을 알 수 있다.
2. 대푯값을 이용한 데이터의 대략적인 개형 알아보기
- 집중화 경향치인 평균, 중앙값, 최빈값은 데이터 분포에 따라 아래와 같은 경향을 갖는다.

- 위 그림은 조금 과장을 한 것이긴 하지만, 데이터는 위와 같은 경향을 띄며, 그 이유는 다음과 같다.
- 최빈값: 가장 많이 등장한 관찰 값이 최빈값이 된다.
- 중앙값: 관찰 값의 빈도에 상관없이 무조건 가운데에 위치한다.
- 평균: 이상치의 영향을 크게 받는다.
- 간단한 도수분포표를 만들어서, 실제로는 어떻게 돌아가는지 확인해보자.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 부드러운 그래프를 그린다.
from scipy.interpolate import make_interp_spline
plt.rc('font', family='NanumGothic')# 최빈값, 중앙값, 평균 계산
def Rep_V(data, column):
raw_list = []
for i in range(len(data)):
X_list = [data.loc[i, "X"]] * data.loc[i, column]
raw_list = raw_list + X_list
median = np.median(raw_list)
mean = np.mean(raw_list)
std = np.std(raw_list)
mode = np.bincount(raw_list).argmax()
return mode, median, mean, std
# 그래프 그리기
def draw_Ske(data, column, title):
"""
도수분포다각형을 부드럽게 그리고, 최빈값, 중앙값, 평균을 점으로 찍고, 선을 그린다.
"""
x = data["X"].to_numpy()
y = data[column].to_numpy()
fig = plt.figure(figsize=(10, 6))
# 부드러운 그래프를 그린다.
model=make_interp_spline(x,y)
xs=np.linspace(np.min(index_list),np.max(index_list),100)
ys=model(xs)
plt.plot(xs, ys)
# 최빈값, 중앙값, 평균 그리기
mode, median, mean, std = Rep_V(data, column)
plt.scatter(mode, 1, c = "r", s = 100)
plt.axvline(x=mode, c = "r", linewidth = 1, alpha = 0.5)
plt.annotate('최빈값', xy=(mode+1, 1), xytext=(mode + 10, 0.5), fontsize = 15,
arrowprops=dict(facecolor='black', width=1, headwidth=8))
plt.scatter(median, 3, c = "g", s = 100)
plt.axvline(x=median, c = "g", linewidth = 1, alpha = 0.5)
plt.annotate('중앙값', xy=(median+1, 3), xytext=(median + 10, 3.2), fontsize = 15,
arrowprops=dict(facecolor='black', width=1, headwidth=8))
plt.scatter(mean, 5, c = "y", s = 100)
plt.axvline(x=mean, c = "y", linewidth = 1, alpha = 0.5)
plt.annotate('평균', xy=(mean+1, 5), xytext=(mean + 10, 6), fontsize = 15,
arrowprops=dict(facecolor='black', width=1, headwidth=8))
plt.title(title, fontsize = 20, pad = 15)
plt.xlabel("$X$", fontsize = 15, labelpad = 10)
plt.ylabel("$f$", rotation = 0, fontsize = 15, labelpad = 10)
plt.show()- 함수 Rep_V(data, column)는 도수분포표를 본래 데이터 셋으로 되돌리고, 최빈값, 중앙값, 평균과 같은 대푯값을 계산하는 함수다.
- 데이터의 양이 지나치게 많아, 컴퓨터가 이를 감당하지 못하는 경우에는 의도적으로 도수분포표를 만들어 대푯값을 계산할 수도 있으나, 위와 같이 데이터의 양이 적은 경우, 도수분포표를 본래 데이터 셋으로 되돌리는 것이 더 쉽다.
index_list = [0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
freq1_list = [1, 3, 6, 11, 17, 24, 17, 11, 6, 3, 1]
freq2_list = [1, 2, 3, 6, 10, 14, 20, 25, 15, 3, 1]
freq3_list = [1, 3, 15, 25, 20, 14, 10, 6, 3, 2, 1]
DF = pd.DataFrame({"X":index_list, "f1":freq1_list, "f2":freq2_list, "f3":freq3_list})DF
2.1. 대칭 분포
draw_Ske(DF, "f1", "1. 대칭분포")
- 대칭 분포인 경우, "평균 = 중앙값 = 최빈값"인 것을 볼 수 있다.
2.2. 왼쪽 꼬리 분포
draw_Ske(DF, "f2", "2. 왼쪽꼬리분포")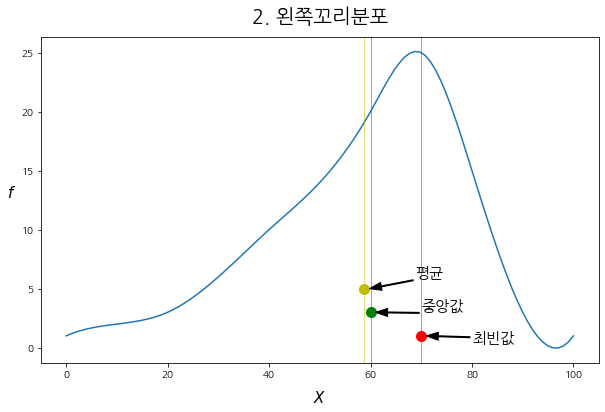
- 왼쪽 꼬리 분포인 경우, "평균 < 중앙값 < 최빈값"이 되는 것을 볼 수 있다.
2.3. 오른쪽 꼬리 분포
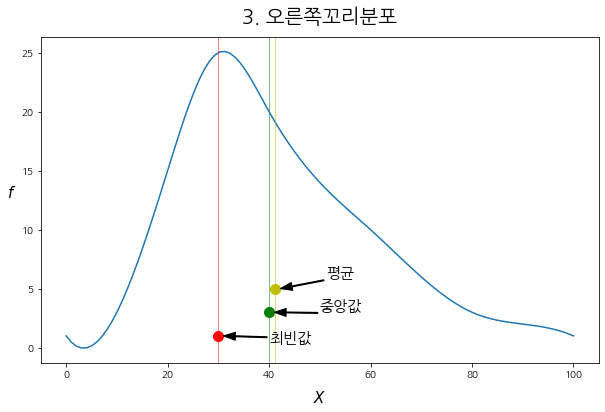
- 오른 꼬리 분포인 경우, "평균 > 중앙값 > 최빈값"이 되는 것을 볼 수 있다.
3. 피어슨의 비대칭 계수(Pearson's skewness coefficients)
칼 피어슨(Karl Pearson)이 만든, 피어슨의 비대칭 계수는, 위에서 본 분포가 좌, 우로 치우치는 경우 평균, 중앙값, 최빈값이 일정한 크기로 순서를 갖는 성질을 이용해서 만든 것이다.
- 피어슨의 비대칭 계수는 평균에 대하여, 최빈값이나 중앙값을 뺀 값을 표준 편차로 나눠서 구한다.
- 피어슨의 비대칭 계수를 구하는 방법은 크게 3가지가 있다.
◎ 피어슨의 제1 비대칭도 계수: $SK_1 = \frac{\bar{X} - mode}{S}$
◎ 피어슨의 제2 비대칭도 계수: $SK_2 = \frac{3(\bar{X} - mode)}{S}$
◎ 피어슨의 제3 비대칭도 계수: $SK_3 = \frac{3(\bar{X} - median)}{S}$
- 위 비대칭도 계수들은 평균과 다른 대푯값의 거리를 얼마나 민감하게 볼 것인가에 대하여 다르게 만들어진 것임을 볼 수 있다.
- 일반적으로 사용하는 것은 피어슨의 제3 비대칭도 계수다.
- 단순한 해석 방법은 3가지 모두 동일하다.
3.1. 피어슨의 비대칭 계수 보는 방법
- 비대칭도 계수가 0이 나오는 경우, 평균과 중앙값(최빈값)이 같으므로, 분포가 치우쳐지지 않음을 알 수 있다.
- 비대칭도 계수가 양수인 경우, 평균보다 중앙값이 작으므로, 오른쪽 꼬리 분포이다.
- 비대칭도 계수가 음수인 경우, 평균보다 중앙값이 크므로, 왼쪽 꼬리 분포이다.
- 비대칭도 계수가 클수록, 한쪽으로 치우친 정도가 크다는 소리다.
- 비대칭도 계수가 0~1 사이인 경우, 1 표준편차보다 분자(평균과 대푯값의 거리에 3을 곱한 값)가 작다는 의미이므로, 치우친 정도가 작다는 소리다.
- 이를 이용하여, 서로 다른 분포에 대하여, 치우친 정도를 비교할 수도 있다(표준편차로 나누었으므로, 단위도 사라진다.).
3.2. 파이썬으로 피어슨의 비대칭 계수를 구현해보자.
- 기존 도수분포표에 보다 치우친 새로운 도수를 추가하여 비교해보자.
index_list = [0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
freq1_list = [1, 3, 6, 11, 17, 24, 17, 11, 6, 3, 1]
freq2_list = [1, 2, 3, 6, 10, 14, 20, 25, 15, 3, 1]
freq3_list = [1, 3, 15, 25, 20, 14, 10, 6, 3, 2, 1]
freq4_list = [1, 1, 2, 3, 5, 7, 10, 16, 23, 26, 6]
DF = pd.DataFrame({"X":index_list, "f1":freq1_list, "f2":freq2_list, "f3":freq3_list, "f4":freq4_list})
DF
- 피어슨의 비대칭도 계수를 구하는 함수를 만들고, 각 변수의 도수들을 비교해보자.
- 각 칼럼의 최빈값, 중앙값, 평균, 표준편차를 출력해보자.
>>> for column in ["f1", "f2", "f3", "f4"]:
>>> mode, median, mean, std = Rep_V(DF, column)
>>> print(f"column: {column} \n 최빈값:{mode}, 중앙값: {median}, 평균: {mean}, 표준편차: {np.round(std,2)}")
>>> print("----"*20)
column: f1
최빈값:50, 중앙값: 50.0, 평균: 50.0, 표준편차: 19.39
--------------------------------------------------------------------------------
column: f2
최빈값:70, 중앙값: 60.0, 평균: 58.8, 표준편차: 19.2
--------------------------------------------------------------------------------
column: f3
최빈값:30, 중앙값: 40.0, 평균: 41.2, 표준편차: 19.2
--------------------------------------------------------------------------------
column: f4
최빈값:90, 중앙값: 80.0, 평균: 71.9, 표준편차: 21.06
--------------------------------------------------------------------------------
- 1번부터 3번까지 피어슨의 비대칭 계수를 계산하는 함수를 만들고, 계수를 계산해보자.
def P_SK(data, column, key):
mode, median, mean, std = Rep_V(DF, column)
if key == 1:
result = (mean - mode)/std
elif key == 2:
result = 3*(mean - mode)/std
elif key == 3:
result = 3*(mean - median)/std
return result>>> for column in ["f1", "f2", "f3", "f4"]:
>>> print(f"column: {column}")
>>> for key in range(1,4):
>>> P_SK_value = P_SK(DF, column, key)
>>> print(f"피어슨의 제 {key} 비대칭도 계수 = {np.round(P_SK_value, 4)}")
>>> print("----"*20)
column: f1
피어슨의 제 1 비대칭도 계수 = 0.0
피어슨의 제 2 비대칭도 계수 = 0.0
피어슨의 제 3 비대칭도 계수 = 0.0
--------------------------------------------------------------------------------
column: f2
피어슨의 제 1 비대칭도 계수 = -0.5834
피어슨의 제 2 비대칭도 계수 = -1.7502
피어슨의 제 3 비대칭도 계수 = -0.1875
--------------------------------------------------------------------------------
column: f3
피어슨의 제 1 비대칭도 계수 = 0.5834
피어슨의 제 2 비대칭도 계수 = 1.7502
피어슨의 제 3 비대칭도 계수 = 0.1875
--------------------------------------------------------------------------------
column: f4
피어슨의 제 1 비대칭도 계수 = -0.8596
피어슨의 제 2 비대칭도 계수 = -2.5787
피어슨의 제 3 비대칭도 계수 = -1.154
--------------------------------------------------------------------------------- 대칭 분포인 f1은 비대칭도 계수가 0이 나왔다.
- 왼쪽 꼬리 분포인 f2는 비대칭도 계수가 모두 음수가 나왔다.
- 오른쪽 꼬리 분포인 f3는 비대칭도 계수가 모두 양수가 나왔다.
- 새로 만든 f2의 비대칭도 계수는 모두 음수가 나왔다.
- 수치가 제법 다르므로, f2와 f4를 시각화하여, 직접 비교해보자.
3.3. 시각화하여 비대칭도 비교
- 위에서 만든 도수분포와 최빈값, 중앙값, 평균을 그려주는 함수인 draw_Ske를 약간 변형하여, 4개 칼럼에 대해 subplot으로 그려보도록 하자.
data = DF
x = data["X"].to_numpy()
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(16,12))
ax = axes.ravel()
column_list = ["f1", "f2", "f3", "f4"]
for i, column in enumerate(column_list):
y = data[column].to_numpy()
# 부드러운 그래프를 그린다.
model=make_interp_spline(x,y)
xs=np.linspace(np.min(index_list),np.max(index_list),100)
ys=model(xs)
ax[i].plot(xs, ys)
title = column_list[i] + "의 분포"
ax[i].set_title(title, fontsize=20, fontweight="bold")
# 최빈값, 중앙값, 평균 그리기
mode, median, mean, std = Rep_V(data, column)
ax[i].scatter(mode, 1, c = "r", s = 100)
ax[i].axvline(x=mode, c = "r", linewidth = 1, alpha = 0.5)
ax[i].annotate('최빈값', xy=(mode+1, 1), xytext=(mode + 10, 0.5), fontsize = 15,
arrowprops=dict(facecolor='black', width=1, headwidth=8))
ax[i].scatter(median, 3, c = "g", s = 100)
ax[i].axvline(x=median, c = "g", linewidth = 1, alpha = 0.5)
ax[i].annotate('중앙값', xy=(median+1, 3), xytext=(median + 10, 3.2), fontsize = 15,
arrowprops=dict(facecolor='black', width=1, headwidth=8))
ax[i].scatter(mean, 5, c = "y", s = 100)
ax[i].axvline(x=mean, c = "y", linewidth = 1, alpha = 0.5)
ax[i].annotate('평균', xy=(mean+1, 5), xytext=(mean + 10, 6), fontsize = 15,
arrowprops=dict(facecolor='black', width=1, headwidth=8))
plt.tight_layout()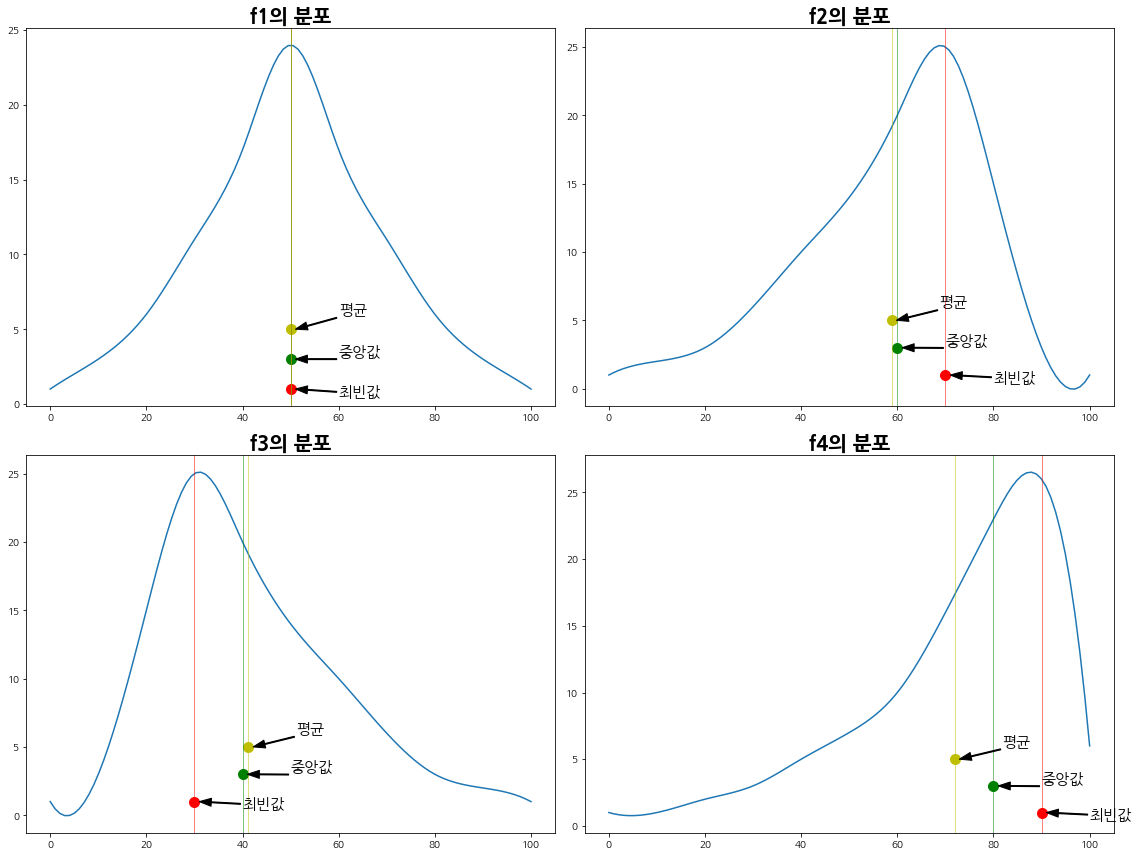
- 위에서 만들었던, 피어슨의 3 비대칭도 계수로 f2와 f4를 비교해보자.
# 치우침이 비교적 작은 f2의 피어슨 비대칭도 계수
>>> P_SK(DF, "f2", 3)
-0.18752034836405185
# 치우침이 비교적 큰 f4의 피어슨 비대칭도 계수
>>> P_SK(DF, "f4", 3)
-1.154019976254971- f2와 f4의 피어슨 비대칭도 계수를 절댓값으로 비교해보면, f4가 더 큰 것을 알 수 있다.
- 위 결과는 평균과 중앙값의 거리가 f2보다 f4가 더 멀다는 것을 의미하며, 이는 f4가 f2보다 한쪽에 더 치우쳐져 있음을 보여준다.
- 위 그래프를 보면 알 수 있듯, f2의 분포보다 f4의 분포가 오른쪽으로 더 데이터가 몰려있음을 알 수 있다.
4. 왜도(Skewness)
- 왜도는 위에서 본 피어슨의 비대칭 계수(Pearson's skewness coefficients)와 같은 분포가 어디에 치우쳐져 있는 지를 보는 보다 더 대표적인 방법이다.
- 사실 왜도를 보다 간략화시킨 것이 피어슨의 비대칭 계수로, 왜도를 보는 방법은 피어슨의 비대칭 계수와 동일하다.
- 음의 왜도(Negative skewness): 왜도에서는 왼쪽에 긴 꼬리를 갖는 왼쪽 꼬리 분포를, 음의 왜도나 좌비대칭형(Skewed left)이라 부른다.
- 양의 왜도(positive skewness): 왜도에서는 오른쪽에 긴 꼬리를 갖는 오른쪽 꼬리 분포를, 양의 왜도나 우비대칭형(Skewed right)이라 부른다.
- 왜도는 각 관찰 값의 편차에 표준편차를 나눈 값에 3 제곱을 하여 합친 값이다.
- 왜도는 모집단의 왜도와 표본 왜도를 구하는 공식이 약간 다르다.
◎ 표본 왜도
$$b_1 = \frac{m_3}{S^3} = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^3}{[\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2]^{\frac{3}{2}}} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})^3}{nS^3}$$
◎ 모집단의 왜도
$$G_1 = \frac{n^2}{(n-1)(n-2)}b_1 = \frac{n}{(n-1)(n-2)}\sum_{i=1}^{n}(\frac{x_i - \bar{x}}{S})^3$$
- 모집단의 평균, 표준편차 등을 알 수 없기 때문에 표본집단을 이용하여, 모집단의 왜도를 추정한다.
4.1. 파이썬을 사용하여 왜도를 구해보자.
- 위에서 만든 DF에 대하여 왜도를 구해보도록 하자.
- 모집단의 왜도를 구하도록 해보자.
# 도수분포표의 도수를 list로 변환한다.
def freqT2list(data, column):
result = []
for i in range(len(data)):
X_list = [data.loc[i, "X"]] * data.loc[i, column]
result = result + X_list
return result
# 왜도 계산
def skewness(data, column):
target = np.array(freqT2list(data, column))
n = len(target)
mean = np.mean(target)
std = np.std(target, ddof=1)
return n/((n-1)*(n-2))*np.sum(((target - mean)/std)**3)>>> for column in ["f1", "f2", "f3", "f4"]:
>>> skew = skewness(DF, column)
>>> print(f"column:{column}, 왜도: {skew}")
column:f1, 왜도: 1.0985509210885902e-16
column:f2, 왜도: -0.704757133477093
column:f3, 왜도: 0.7047571334770931
column:f4, 왜도: -1.1553356711140326- 대칭 분포인 f1의 왜도는 1.0985509210885902e-16로 나왔다.
- 이는 0.0000000000000001098으로, 소수점 아래 16번째 자리에서 처음으로 e 앞에있는 숫자가 나온다는 의미로, 매우 작은 수로, 파이썬의 계산 방식 등으로 인해 이런 문제가 발생할 수 있으니, 깔끔하게 소숫점 아래 6자리에서 반올림을 해서 다시 보자.
>>> for column in ["f1", "f2", "f3", "f4"]:
>>> skew = np.round(skewness(DF, column), 6)
>>> print(f"column:{column}, 왜도: {skew}")
column:f1, 왜도: 0.0
column:f2, 왜도: -0.704757
column:f3, 왜도: 0.704757
column:f4, 왜도: -1.155336- 왜도 역시, 피어슨의 비대칭 계수처럼 음과 양으로 데이터가 어디에 모여있는지 알 수 있다. 간단하게 음수면 긴 꼬리가 음수의 방향, 양수면 긴 꼬리가 양수의 방향에 있다고 생각하자.
- 왜도가 커질수록 분포가 크게 치우친 것이다.
4.2. Scipy로 왜도를 구해보자
- scipy의 stats 모듈에 있는 skew 함수를 사용해서 더 쉽게 왜도를 구할 수 있다.
from scipy import stats>>> for column in ["f1", "f2", "f3", "f4"]:
>>> target = np.array(freqT2list(DF, column))
>>> skew = stats.skew(target)
>>> print(f"column:{column}, 왜도: {skew}")
column:f1, 왜도: 0.0
column:f2, 왜도: -0.6941414183237987
column:f3, 왜도: 0.694141418323799
column:f4, 왜도: -1.137932918011734- scipy.stats.skew(array): 왜도를 구한다.
- scipy로 구한 왜도와 직접 만든 공식과 그 값이 꽤 다른 것을 알 수 있다.
- 이는, scipy의 왜도는 표본 왜도를 구하며, 사용하는 공식이 약간 다르므로, 표준편차를 모 표준편차로 구했기 때문이다.
- 이에 맞게 공식을 고쳐서 출력해보자.
# 왜도 계산
def skewness(data, column):
target = np.array(freqT2list(data, column))
n = len(target)
mean = np.mean(target)
std = np.std(target, ddof=0)
return 1/n*np.sum(((target - mean)/std)**3)>>> for column in ["f1", "f2", "f3", "f4"]:
>>> skew = np.round(skewness(DF, column), 6)
>>> print(f"column:{column}, 왜도: {skew}")
column:f1, 왜도: 0.0
column:f2, 왜도: -0.694141
column:f3, 왜도: 0.694141
column:f4, 왜도: -1.137933- 왜도가 돌아가는 방식에 대해 알 필요는 있으나, 개인적으로는 이 부분을 심화시키는 것은 시간낭비라고 판단된다.
- 왜도는 분포의 형태를 대략적으로 아는 도구이므로, 보다 정확한 도구를 사용하는 것보단, 동일한 도구를 이용해서 평가하는 것이 중요하다고 판단되므로, scipy.stats의 skew함수를 사용하도록 하자.
5. 첨도(Kurtosis)
- 왜도가 데이터가 어느 쪽에 쏠려 있는지를 보는 용도라면, 첨도는 데이터가 얼마나 모여있는지를 가리킨다.
- 첨도가 클수록 데이터는 한 곳에 매우 많이 모여 있고, 첨도가 작을수록 데이터가 흩어져 있다.
- 첨도 = 0: 표준 정규분포다.
- 첨도 > 0: 표준 정규분포보다 평균에 데이터가 더 많이 모여 있는 뾰족한 형태다.
- 첨도 < 0: 표준 정규분포보다 평균에서 데이터가 더 흩어진 완만한 형태다.
- 첨도가 크다할지라도, 분산이 더 큰 경우, 완만한 그래프가 나타날 수 있으므로, 분산이 동일한 분포끼리 비교해야 한다.
- 첨도는 각 관찰 값과 표본 평균의 편차에 표본 표준편차를 나눈 값에 4 제곱을 해서 구한다.
- 첨도의 기준은 정규분포가 되며, 정규분포의 첨도는 3이지만, 이를 보기 쉽도록, 3을 빼서, 0으로 보정해준다.
◎ 표본 첨도
$$g_2 = \frac{m_4}{m_{2}^2} - 3 = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^4}{[\frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2]^2} - 3 = \frac{n}{(n-1)^2}\sum_{i=1}^{n}(\frac{x_i-\bar{x}}{S})^4 - 3$$
◎ 모집단의 첨도(불편추정량)
$$G_2 = \frac{n-1}{(n-2)(n-3)}[(n+1)g_2 + 6]) = \frac{n(n+1)}{(n-1)(n-2)(n-3)}\sum_{i=1}^{n}(\frac{x_i - \bar{x}}{S})^4 - 3\frac{(n-1)^2}{(n-2)(n-3)}$$
5.1. 파이썬으로 첨도를 구현해보자.
- 넘파이를 이용하여, 평균은 0이고, 표준편차 1인 표준 정규분포를 만들어보자.
np.random.seed(1234)
Normal_Dist = np.random.normal(loc = 0, scale = 1, size = 10000)plt.rc('font', family='monospace')- 위에서 한글을 사용하기 위해 폰트를 나눔 고딕으로 설정하는 경우 음수의 "-" 부호가 깨지게 되므로, 폰트를 바꿔주었다.
fig = plt.figure(figsize=(10, 6))
plt.hist(Normal_Dist, bins = 60, density=True)
plt.show()
5.2. 첨도 함수를 만들어보자.
5.2.1. Numpy 라이브러리의 함수를 사용해서 만들어보자.
# 첨도
def Kurt(array):
mean = np.mean(array)
std = np.std(array, ddof = 1)
n = len(array)
g2 = n/(n-1)**2*np.sum(((array - mean)/std)**4) - 3
G2 = ((n-1)/((n-2)*(n-3)))*((n+1)*g2 + 6)
return G2>>> Kurt(Normal_Dist)
-0.06547331601746852
5.2.2. scipy.stats 모듈의 kurtosis() 함수를 사용해서 만들어보자.
from scipy import stats>>> stats.kurtosis(Normal_Dist)
-0.06604052394826398- scipy와 numpy로 직접 만든 첨도의 결과가 약간 다른 것을 알 수 있다.
- 이는, scipy에서는 Kurt함수의 G2가 아닌 g2로 계산되기 때문으로, 즉 모집단의 첨도가 아닌 표본 첨도가 계산된다는 소리다.
def Kurt_g2(array):
mean = np.mean(array)
std = np.std(array, ddof = 1)
n = len(array)
g2 = n/(n-1)**2*np.sum(((array - mean)/std)**4) - 3
return g2>>> Kurt_g2(Normal_Dist)
-0.06604052394826398
>>> stats.kurtosis(Normal_Dist) == Kurt_g2(Normal_Dist)
True
5.3. 무작위로 생성한 표준정규분포의 난수를 더 표준정규분포에 가깝게 해 보자.
- 위에서 만든 표준정규분포의 난수는 크기가 10,000으로, 실제 표준정규분포와 거리가 있다.
- 이번에는 난수의 크기를 1,000,000으로 해서 실제 표준정규분포에 더 가깝게 만들어보자.
(데이터의 양이 엄청나기 때문에 컴퓨터에 부담이 가는 경우 수를 조금 줄이자)
np.random.seed(1234)
Normal_Dist = np.random.normal(loc = 0, scale = 1, size = 1000000)fig = plt.figure(figsize=(10, 6))
plt.hist(Normal_Dist, bins = 60, density=True)
plt.show()
>>> Kurt_g2(Normal_Dist)
0.0006377812832605301- 난수의 크기가 10,000일 때보다 표준정규분포에 근사하게 되니 첨도가 0에 더 가까워지는 것을 볼 수 있다.
- 그러나, 난수를 이용해서인지 크기를 늘린다고 해서 선형으로 0에 더 가깝게 가지는 않는다.
5.4. 표준 편차가 1로 동일하지만, 크기가 매우 작아 표준 정규분포와 거리가 먼 난수를 생성해보자.
np.random.seed(1234)
Normal_Dist = np.random.normal(loc = 0, scale = 1, size = 10)fig = plt.figure(figsize=(10, 6))
plt.hist(Normal_Dist, density=True)
plt.show()
>>> Kurt_g2(Normal_Dist)
-0.6112182077094723- 이번에 생성한 데이터는 평균이 1, 표준편차가 1로 이전의 난수와 동일하지만, 크기가 10으로 매우 작아, 분산만 동일하지 정규분포로 보기 힘든 데이터를 생성해보았다.
- 이 경우, 첨도는 -0.611로 기존에 생성한 분포보다 더 완만하다는 것을 알 수 있다.
5.5. 표준편차가 다른 분포들을 만들고, 첨도를 비교해보자.
np.random.seed(1234)
Normal_Dist0 = np.random.normal(loc = 0, scale = 0.4, size = 100000)
Normal_Dist1 = np.random.normal(loc = 0, scale = 1, size = 100000)
Normal_Dist2 = np.random.normal(loc = 0, scale = 2, size = 100000)fig = plt.figure(figsize=(10, 6))
plt.hist(Normal_Dist0, density=True, bins=60, alpha=0.5, label="N(0, 0.5)")
plt.hist(Normal_Dist1, density=True, bins=60, alpha=0.5, label="N(0, 1)")
plt.hist(Normal_Dist2, density=True, bins=60, alpha=0.5, label="N(0, 2)")
plt.legend(loc="upper right")
plt.show()
>>> Ku0 = Kurt_g2(Normal_Dist0)
>>> Ku1 = Kurt_g2(Normal_Dist1)
>>> Ku2 = Kurt_g2(Normal_Dist2)
>>> print(f"표준편차가 0.5인 분포의 첨도:{Ku0}")
>>> print(f"표준편차가 1인 분포의 첨도:{Ku1}")
>>> print(f"표준편차가 2인 분포의 첨도:{Ku2}")
표준편차가 0.5인 분포의 첨도:-0.030292593794574607
표준편차가 1인 분포의 첨도:-0.00581814290437066
표준편차가 2인 분포의 첨도:0.01995196078021788- 위 분포만 본다면, 표준 정규분포에 가장 가까운 노란색보다 더 뾰족하게 솟은 파란색 분포가 값이 더 커야 할 것으로 보이지만, 보다 음수에 가까운 것을 알 수 있다.
- 이는 첨도와 표준편차는 별개로 움직이기 때문으로, 위와 같이 표준편차가 다른 경우, 그래프의 개형이 보다 더 뾰족하거나 완만하다 할지라도, 첨도가 별개로 작동하여, 잘못된 판단을 할 위험이 있다.
- 즉, 첨도는 분산이 동일한 상태에서 사용해야, 데이터가 평균에 모인 정도에 대해 제대로 된 비교를 할 수 있다.
'Python으로 하는 기초통계학 > 기본 개념' 카테고리의 다른 글
| 산포도 - 편차: 절대 편차 & 절대 편차를 사용하지 않는 이유 & 변동 계수 (0) | 2021.03.08 |
|---|---|
| 산포도 - 편차: 분산 & 표준 편차 & 표준편차에 (n-1)을 나누는 이유 & 자유도 (0) | 2021.03.05 |
| 산포도(Dispersion) - 범위, 사분위간 범위, 사분위수와 상자 수염 그림 (0) | 2021.03.04 |
| 중심경향치(2) - 산술 평균, 기하 평균, 조화 평균, 모평균과 표본 평균이 같은 이유 (0) | 2021.03.03 |
| 중심경향치(1) - 최빈값, 중앙값 (0) | 2021.03.03 |