728x90
반응형

산포도(Dispersion)
◎ 산포도: 분산도(Degree of dispersion), 변산성(Variability)이라고도 하며, 관찰된 데이터가 흩어져 있는 정도를 말한다.
- 통계학은 기본적으로 데이터가 어디에 모여있고, 얼마나 흩어져 있는지를 통해 데이터를 파악한다고 하였다.
- 지금까지 데이터가 어디에 모이는지에 대한 중심경향치(Center Tendency)를 알아보았으므로, 이번에는 데이터가 얼마나 흩어져있는지를 알 수 있는 산포도(Dispersion)에 대해 알아보겠다.
- 산포도에는 범위(Range), 사분위간 범위(Interquartile range), 분산(Varience), 표준 편차(Standard deviation), 절대 편차(Absolute deviation), 변동 계수(Coefficient of variation) 등이 있다.
- 학습 데이터(참고 포스트: "통계 분석을 위한 데이터 준비")
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
Rawdata = pd.read_csv("Data_for_study.csv")
1. 범위(Range)
◎ 범위(Range): 관찰 값에서 최댓값과 최솟값의 차이다.
$$ range = max - min $$
- 데이터가 흩어진 정도를 보는 가장 간단한 방법으로, 관찰 값이 시작되는 최솟값에서 관찰값이 끝나는 최댓값의 차이다.
- 범위는 구하기 쉽고, 해석하기도 쉬우나, 간단한만큼 많은 단점을 가지고 있다.
- 범위는 이상치(다른 데이터에 비해 지나치게 크거나, 작은 값)의 영향을 너무 심하게 받는다.
- 최댓값에서 최솟값의 차이만 구하므로, 같은 범위를 갖는다고 할지라도 데이터의 분포가 완전히 다를 수 있다.
- 학습 데이터에서 "학업성적", "건강인지"의 범위를 구해보자.
def cal_range(data, column):
target_series = data[column]
return target_series.max() - target_series.min()- pd.Series.min(): 시리즈의 최솟값을 구한다.
- pd.Series.max(): 시리즈의 최댓값을 구한다.
>>> cal_range(Rawdata, "학업성적")
4.0
>>> cal_range(Rawdata, "건강인지")
4.0- "학업성적", "건강인지"의 도수분포표를 이용해, 도수분포다각형(Frequency distribution polygon)을 그려보자.
def FDPolygon(data, column):
freq_table = data[column].value_counts().sort_index()
ratio_x = freq_table.values/sum(freq_table.values)
# 도수분포다각형 그리기
plt.plot(freq_table.index, ratio_x, label = column)
plt.xticks(np.arange(1, len(freq_table.index) + 1))plt.rc('font', family='NanumGothic')
fig = plt.figure(figsize=(8, 6))
FDPolygon(Rawdata, "건강인지")
FDPolygon(Rawdata, "학업성적")
# 그래프 꾸미기
plt.legend(loc = "upper right")
plt.title("건강인지 & 학업성적 도수분포다각형", fontsize = 20, pad = 30)
plt.xlabel("관측값", fontsize = 15, labelpad = 10)
plt.ylabel("비율", rotation = 0, fontsize = 15, labelpad = 20)
plt.show()
- "건강인지", "학업성적" 변수의 범위는 동일하지만, 데이터의 분포는 상당히 다른 것을 알 수 있다.
- 즉, 범위는 한 변수 안의 데이터의 관측값의 시작 값(최솟값)에서 끝 값(최댓값)까지의 간격을 알 수 있지만, 데이터가 어떻게 분포해 있는지 알 수는 없다.
2. 사분위간 범위(Interquartile range, IQR)
◎ 사분위간 범위: 데이터를 25% 단위로 4개의 구간으로 나누는 관측값을 사분위수(Quartile)라 하며, 이 사분위수에서 제1사분위수(Q1)와 제3사분위수(Q3)의 범위가 사분위간 범위다.
$$ IQR = Q3 - Q1 $$
- 사분위수(Quartile):
전체 데이터를 25% 단위로 나눌 수 있는, Q1(1사분위수), Q2(2사분위수), Q3(3사분위수)를 말한다. - 각 사분위수는 각 값의 하위 범위에 대하여, Q1은 25% 이하의 데이터가 존재하는 관측값, Q2는 50% 이하의 데이터가 존재하는 관측값(중위수), Q3는 75% 이하의 데이터가 존재하는 관측값을 말한다.
- 즉, Q1은 제 25 백분위수, Q2는 제 50 백분위수, Q3는 제 75 백분위수이다.
- Q4는 제4사분위로 제 100 백분위수다.
- 사분위간 범위는 산포도이며, 사분위수는 대푯값에 해당한다.
- 중위수, 사분위간 범위는 빈도를 이용해 계산되며, 이상치(지나치게 크거나 작은 값)의 영향을 받는 양 극단의 값 역시, 단순히 빈도로 보므로 이상치의 영향을 받지 않는다.
2.1. 파이썬을 이용해서 사분위수 구하기
2.1.1. pandas 라이브러리 활용
- 키에 대하여 사분위수를 구해보자.
>>> Rawdata.키.quantile(0)
136.0
>>> Rawdata.키.quantile(0.25)
159.1
>>> Rawdata.키.quantile(0.5)
165.0
>>> Rawdata.키.quantile(0.75)
172.0
>>> Rawdata.키.quantile(1)
196.0- pd.Series.quantile(float): 0에서 1 사이의 비율에 대하여, 그 비율의 위치에 해당하는 관찰 값을 반환한다.
- 하위 빈도의 비율에 대해 구하므로, 사분위수가 아닌 하위 60, 80%와 같은 값도 쉽게 구할 수 있다.
>>> Rawdata.키.quantile(0.6)
167.8
>>> Rawdata.키.quantile(0.8)
173.2
2.1.2. Pandas의 기본적인 기술 통계량을 반환하는 함수로도 구할 수 있다.
>>> Rawdata.키.describe()
count 55748.000000
mean 165.527266
std 8.589459
min 136.000000
25% 159.100000
50% 165.000000
75% 172.000000
max 196.000000
Name: 키, dtype: float64- pd.DataFrame.describe(): 데이터 요약을 위한 메서드로, 빈도, 평균, 표준편차, 최솟값, 사분위수, 최댓값을 시리즈로 출력한다.
>>> 키_기술통계량 = Rawdata.키.describe()
>>> 키_기술통계량.loc["25%"]
159.1
>>> 키_기술통계량.loc["75%"]
172.0
>>> 키_기술통계량.loc["mean"]
165.5272655521264
>>> 키_기술통계량.loc["std"]
8.589459420964502- 시리즈로 출력되므로, index를 이용해, 그 인데스에 해당하는 값을 반환하는 loc를 사용하면, 내가 원하는 값만 가지고 올 수 있다.
2.2.2. Numpy를 이용하여 사분위수 구하기
>>> target_array = Rawdata.키.to_numpy()
>>> np.percentile(target_array, 25)
159.1
>>> np.percentile(target_array, 50)
165.0
>>> np.percentile(target_array, 75)
172.0- np.percentile(array, q): q번째 백분위 수를 계산하여, 배열의 q번째 백분위 수를 반환한다.
2.3. 사분위간 범위 구하기
def cal_Interquartile_range(data, column):
target_array = data[column].to_numpy()
return np.percentile(target_array, 75) - np.percentile(target_array, 25)>>> cal_Interquartile_range(Rawdata, "키")
12.900000000000006
3. 사분위수와 상자 수염 그림
◎ 상자 수염 그림(Box-and-whisker plot): 상자 그림(Box plot)이라고도 하며, 다섯 숫자 요약(최솟값, 제1사분위수, 중앙값, 제3사분위수, 최댓값)으로 데이터의 특성을 요약하는 그래프다.
- 다섯 숫자 요약(Five-number summary): 최솟값(min), 제1사분위수(Q1), 중앙값(median), 제3사분위수(Q3), 최댓값(max)으로 전체 데이터를 요약한 것이다.
- 사분위간 범위(IQR)로 몸통을 구성하고, 근접 값들로 꼬리를 구성한다.
- 단위 척도(Step): 1.5 * IQR
- 안 울타리(Inner fence)는 Q1에서 최솟값의 방향으로 1 step만큼 이동한 것이고, Q3에서 최댓값의 방향으로 1 step만큼 이동한 곳에 그린다.
- 바깥 울타리(Outer fence)는 Q1에서 최솟값의 방향으로 2 step만큼 이동한 것이고, Q3에서 최댓값의 방향으로 2 step만큼 이동한 곳에 그린다.
3.1. 상자 수염 그림과 이상값(Outlier)
◎ 이상값(Outlier): 정상 범주에서 벗어난 값으로, 정상 관측값에서 벗어난 값이거나, 지나치게 크거나 작아 정상범위에서 벗어난 값을 의미한다.
- 상자 수염 그림을 이용하면, 이상값을 찾아낼 수 있다.
- 근접값(Adjacent value): 안 울타리 안쪽 값 중 안 울타리에 가장 가까운 값
- 보통 이상값(Mild Outlier): 한쪽 방향에 대하여, 바깥 울타리, 안 울타리 사이의 값
- 극단 이상값(Extreme Outlier): 바깥 울타리 밖에 있는 값
- 근접값은 이상값에 가장 가까운 정상 범위 내 최대·최솟값이며, 이상값은 정상 범위(사분위간 범위)에서 크게 벗어난 값이므로, 연구자의 관점에 따라 데이터에서 제거, 혹은 집단의 재구성 등을 통한 이상값 처리를 해주는 것을 추천한다.
3.2. 상자 수염 그림 그리기
- 주어진 데이터 "키" 변수에 대하여, 상자 수염 그림을 그려보자.
fig = plt.figure(figsize=(10, 8))
plt.boxplot(Rawdata.키.to_numpy())
plt.title("키의 상자 수염 그림", fontsize = 20, pad = 30)
plt.ylabel("키", rotation = 0, fontsize = 15, labelpad = 20)
plt.show()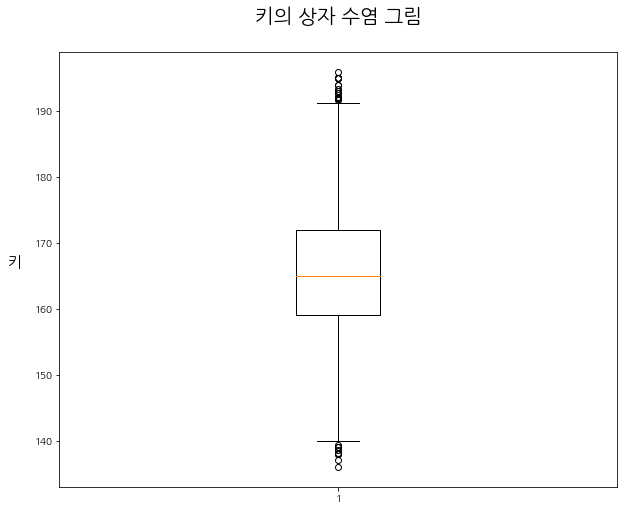
- 위 상자 수염 그림에서 상자(Box)는 사분위간 범위이다.
- 상자(Box) 안의 주황색 선은 중앙값이다.
- 상자 위아래에 달려 있는 'ㅜ', 'ㅗ' 모양의 선은 수염(Whisker)이다.
- 양쪽 수염의 끝은 정상 범위의 최대·최솟값이다.
- 수염 바깥의 동그란 점은 보통 이상값(mild outlier)이다.
- 위 데이터에는 극단 이상값(Extream outlier)이 존재하지 않으므로, 바깥 울타리는 보이지 않는다.
3.3. 상자 수염 그림에서의 정상범위의 최솟값과 최댓값 찾기
- 상자 수염 그림에서 정상범위의 최솟값과 최댓값을 뽑으면, 이상값을 구분할 수 있는 영역을 찾을 수 있다.
- 상자 수염 그림에서 정삼 범위 최솟값은 $Q1 - 1.5*IQR$이며, 최댓값은 $Q3 + 1.5*IQR$이다.
def Outlier_checker(data, column):
target_array = data[column].to_numpy()
Q1 = np.percentile(target_array, 25)
Q3 = np.percentile(target_array, 75)
IQR = Q3 - Q1
norm_min = Q1 - 1.5*IQR
norm_max = Q3 + 1.5*IQR
return norm_min, norm_max>>> Outlier_checker(data, "키")
(139.75, 191.35000000000002)- 위 결과를 볼 때, 키에서 139.75 cm 미만, 191.35cm 초과는 이상값임을 알 수 있다.
728x90
반응형
'Python으로 하는 기초통계학 > 기본 개념' 카테고리의 다른 글
| 산포도 - 편차: 절대 편차 & 절대 편차를 사용하지 않는 이유 & 변동 계수 (0) | 2021.03.08 |
|---|---|
| 산포도 - 편차: 분산 & 표준 편차 & 표준편차에 (n-1)을 나누는 이유 & 자유도 (0) | 2021.03.05 |
| 중심경향치(2) - 산술 평균, 기하 평균, 조화 평균, 모평균과 표본 평균이 같은 이유 (0) | 2021.03.03 |
| 중심경향치(1) - 최빈값, 중앙값 (0) | 2021.03.03 |
| 도수분포표와 시각화 (0) | 2021.03.02 |