728x90
반응형

편차(Deviation)
이전 포스트에서는 관측값과 평균의 차이인 편차를 이용해서 구하는 대표적인 산포도 "분산(Varience)"와 "표준편차(Standard Deviation)에 대해 학습해보았다.
이번 포스트에서는 편차를 이용하는 다른 산포도인 절대 편차(Absolute deviation)와 변동 계수(Coefficient of variation)에 대해 알아보자.
1. 절대 편차(Absolute deviation)
- 절대 편차는 관측값에서 평균(Mean) 또는 중앙값(Median)을 빼고, 그 편차에 절댓값을 취하고, 평균을 구한 것으로, 분산에서 제곱 대신 절댓값을 취한 것이다.
$$ AAD = \frac{1}{N}\sum_{i=1}^{N}\left | x_i - \mu \right | = \frac{\left | x_1 - \mu \right | + \left | x_2 - \mu \right | + \cdots + \left | x_N - \mu \right |}{N} $$
- 평균 절대 편차(Average Absolute Deviation, AAD): 각 관측값에 평균을 빼고, 편차 절댓값의 평균을 구하는 경우로, 평균 편차(Mean Deviation), 절대 편차(Absolute Deviation)라고도 한다.
- 중앙값 절대 편차(Median Absolute Deviation, MAD): 각 관측값에 중앙값을 빼고, 편차 절댓값의 평균을 구하는 방식이다.
- 최소 절대 편차(Least Absolute Deviation, LAD): 회귀분석에서 최소제곱법(LSA)에 대응되는 기법으로, 절대 오차의 합이 최소가 되는 해를 찾는 기법이다.
- 분산은 이상치가 존재하는 경우, 편차를 제곱시키므로 편차가 증폭될 수 있다. 절대 편차를 하는 경우, 제곱을 하지 않으므로, 이상치 존재로 인한 편차 증폭 문제를 보완할 수 있다.
- 예) 평균 $100$, 이상치가 $10000$인 경우, $9,900^2 = 9,8010,000$이 되어 값이 매우 커지게 된다.
1.1. 파이썬과 절대 편차
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt- 해당 데이터를 사용하여, 절대 편차를 만들어보자.
- 해당 데이터 설명은 이전 포스트 "통계 분석을 위한 데이터 준비"를 참고 하기 바란다.
1.1.1. numpy를 사용하여 절대 편차(AD) 만들기
- 데이터 분석에 주로 사용되는 라이브러리인 numpy나 pandas는 따로 해당 함수를 제공하지 않는다.
- 그러나, numpy를 사용해서 만들면, 난이도도 쉽고, numpy 기본 함수의 속도가 매우 빨라, 성능도 나쁘지 않다.
def AD(data, column, way, dof = 1):
target_array = data[column].to_numpy()
if way == "mean":
key_value = np.mean(target_array)
elif way == "median":
key_value = np.median(target_array)
return np.sum(np.abs(target_array - key_value))/(len(target_array) - dof)- way로 "mean"이 들어오는지, "median"이 들어오는지에 따라 평균 절대 편차나 중앙값 절대 편차가 수행된다.
- np.abs(array): array에 있는 모든 원소를 양수로 만든다.
- 표본 집단에 대한 분석을 가정하여, 자유도로 나눈다.
>>> AD(Rawdata, "키", "mean")
7.0767022252239355
>>> AD(Rawdata, "키", "median")
7.046750497784634
>>> AD(Rawdata, "몸무게", "mean")
10.159191145859118
>>> AD(Rawdata, "몸무게", "median")
10.00470697974779
2. 절대편차(AAD)가 아닌 표준편차(Standard Deviation)를 사용하는 이유
- 절대편차를 사용하지 않는 이유는 총 4가지가 있다.
- 편차란 유클리디안 거리(Euclidean distance)에서, 각 관측값이 특정값(평균)으로부터 떨어져 있는 거리를 의미하기 때문이다.
- 절대편차의 최솟값은 평균이 아닌 중앙값이다.
- 절대편차는 미분되지 않는다.
- 절댓값을 연산하기 위해선 공식이 복잡해진다.
2.1. 편차와 유클리디안 거리(Euclidian distance)
- 절대편차를 사용하지 않는 이유를 알기 위해선, 편차의 의미에 대해 알 필요가 있다.
- "편차는, 관측값이 특정값(평균)으로부터 떨어진 거리"인데, 이를 구체적으로 보기 위해 고등학교 때 배웠던, 두점 사이의 거리 공식을 보도록 하자.

- 위 두 점 사이의 거리는 2차원에서의 거리다. 이번에는 n차원의 공간에서 두 점간의 거리를 알아내는 공식인 유클리디안 거리(Euclidan distance)에 대해 알아보자. 위 2차원에서의 거리 공식과 개념이 매우 유사하다.

- 위 유클리디안 거리에서 점 $B_i$를 평균인 $\mu$로 만든다면, 우리가 아는 분산(Variance) 공식이 나온다.
- 그러나, 위 유클리디안 거리는 n차원에서의 두 점 사이의 거리를 의미한다. 때문에 1차원에서라면, 절대 평균 편차 공식을 사용해도 되지 않는가 하는 의문이 들 수 있다.
2.2. 절대 편차의 최솟값은 평균이 아닌 중앙값이다.
- "편차는 관측값들이 특정값으로부터 떨어진 정도(거리)"라고 하였다.
- 이 특정값을 우리는 대푯값(Representative value)라고 하며, 대푯값은 어떤 데이터를 대표하는 값이다.
- 이번에는 관측값의 집합$X = (1, 2, 5)$가 있다고 가정하고, 이것을 분산으로 구할 때와, 절대편차로 구할 때에 따라, 임의의 대푯값 $R$이 분산($\sigma^2$)과 절대편차에 대하여 어떠한 함수의 형태를 그리는지 보도록 하자.
# 분산인 경우
def f(x):
return((1-x)**2 + (2-x)**2 + (5-x)**2)/3
# 절대 편차인 경우
def h(x):
return(np.abs(1-x) + np.abs(2-x) + np.abs(5-x))/3def draw_Function(f, key):
# 대푯값에 대한 시각화를 해보자.
R = np.arange(0, 10, 0.001)
y = f(R)
# 최솟값을 구한다.
min_y = y.min()
min_x = R[np.where(y == min_y)][0]
# 그래프 그리기
plt.rc('font', family='NanumGothic')
fig = plt.figure(figsize=(8, 6))
# 함수 f의 시각화
plt.plot(R, y)
# y 값에서의 최솟값
plt.scatter(min_x, min_y, color="r",s = 100)
# 그래프 꾸며주기
plt.title(f"{key}에 대한 대푯값", fontsize = 20, pad = 30)
plt.xlabel("대푯값", fontsize = 15, labelpad = 10)
plt.ylabel(f"{key}", rotation = 0, fontsize = 15, labelpad = 20)
plt.show()
print(f"({np.round(min_x, 3)}, {np.round(min_y, 3)})에서 함수 f(x)는 최솟값을 갖는다.")2.2.1. 분산에 대한 대푯값의 그래프
>>> draw_Function(f, "분산")
(2.667, 2.889)에서 함수 f(x)는 최솟값을 갖는다.
- 대푯값 R에 대한 분산($\sigma^2$)의 그래프를 그렸을 때, 이차 함수 형태를 그리는 것을 볼 수 있다.
- 분산의 최솟값은 2.889이며, 이는 대푯값(R) 2.667이다.
- 관측값 X = [1, 2, 5]의 평균은 다음과 같다.
>>> np.mean([1,2,5])
2.6666666666666665
- 관측값의 평균과 분산이 최솟값을 갖는 대푯값은 일치한다.
(약간의 차이가 있는 이유는, 그래프 생성 시, np.arange(start, end, by)에 대하여, by의 간격이 0.001로 이산된 부분이 생겼기 때문이다. by를 작게 할 수도록 평균과 근사해진다.) - 즉, 분산에 있어 대푯값은 평균이다.
2.2.2. 절대편차에 대한 대푯값의 그래프
>>> draw_Function(h, "절대편차")
(2.0, 1.333)에서 함수 f(x)는 최솟값을 갖는다.
- 절대편차의 개형은 꺾은선 그래프와 같은 형태를 그린다.
- 절대편차에서의 최솟값은 대푯값 2.0에서 존재한다.
- 대푯값 2.0은 관측값의 집합 X=[1,2,5]에서 중앙값(Median)인 2이다.
2.2.3. 절대편차에 대한 대푯값의 그래프에서 집합의 원소가 짝수일 때
- X = [1, 2, 5, 7]이 관측값의 집합이라 가정해보자.
def h1(x):
return(np.abs(1-x) + np.abs(2-x) + np.abs(5-x) + np.abs(7-x))/4>>> draw_Function(h1, "절대편차")
(2.0, 2.25)에서 함수 f(x)는 최솟값을 갖는다.
- 집합의 원소가 짝수인 경우, 그래프의 개형에서 아래쪽이 평평해진다.
- 대푯값 R이 한 점이 아닌 선이 되었으므로, 선에 대한 대푯값으로 중앙값을 구해보자.
>>> R = np.arange(0, 10, 0.001)
>>> y = h1(R)
>>> min_y = y.min()
>>> min_x = R[np.where(y == min_y)]
>>> print("절대편차에 대한 대푯값의 중앙값:", str(np.median(min_x)))
절대편차에 대한 대푯값의 중앙값: 3.5
>>> print("집합 X의 중앙값:", str(np.median([1,2,5,7])))
집합 X의 중앙값: 3.5- 집합의 개수가 짝수일 때도, 대푯값이 중앙값인 것을 알 수 있다.
2.2.4. 정리
- 위 결과를 볼 때, 절대 편차는 관측값으로부터 중앙값까지의 거리의 평균인 것임을 알 수 있다.
- 즉, 차원이 1개라고 가정한다 할지라도, 절대 편차의 대푯값은 중앙값이므로, 분산처럼 평균에서 각 원소까지의 거리 제곱의 평균을 구할 수 있는 것이 아니라, 중앙값에서 각 원소까지의 거리의 절댓값의 평균이 되게 되어, 의미가 달라지게 된다.
- 또한, 절대 편차를 사용할 때, 중앙값 절대 편차(MAD)를 사용하게 되는 이유가 바로 위와 같다.
2.3. 절대편차는 미분되지 않는다.
- 위에서 만든 절대편차의 대푯값 그래프를 가지고 와보자.
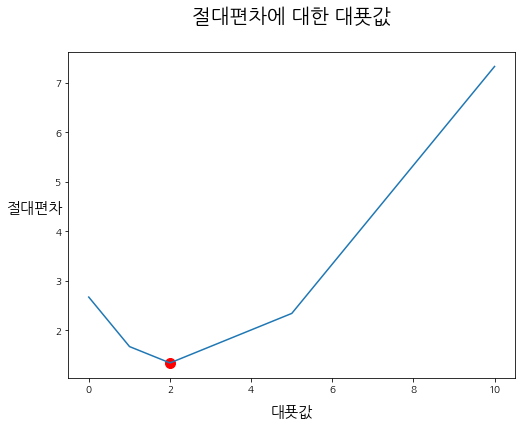
- 미분을 위한 기본 조건은 좌 미분과 우 미분이 같아야 한다는 것인데, 보시다시피 절대편차는 매끈한 곡선이 아니므로, 좌 미분과 우 미분이 동일하지 않은 점이 반드시 존재한다.
- 미분이 되지 않는다는 것은 산포도의 관점에서는 그다지 중요한 이유가 아니지만, 손실함수의 미분을 통한 최적해를 찾아가는 과정인 딥러닝의 학습 부분에서는 상당히 중요한 이유가 된다.
2.4. 절댓값 연산을 위해선 연산이 복잡해진다.
- 절댓값 연산을 위해선, 각 편차의 부호를 확인하는 과정이 필요하다.
- 반면에 분산은 편차를 일괄적으로 제곱하여 모든 부호가 양으로 만들기 때문에 연산이 아주 간단해진다.
2.5. 정리
- 위 내용을 줄여보면, 산포도라는 대상을 위해 절대 편차를 사용하는 것에는 문제가 없으나, 그 기준을 평균이 아닌 중앙값(Median)으로 잡는 것이 좋으며, 중간값 절대 편차(MAD)를 사용한다 할지라도, 태생적인 한계점이 많으므로, 중간값 절대 편차보다는 분산을 사용하는 것이 좋다.
3. 변동 계수(Coefficient of Variation, CV)
- 변동 계수는 표준 편차를 표본 평균이나 모 평균과 같은 산술 평균으로 나눈 값이다.
$$ CV = \frac{S}{\bar{X}} $$
- 변동 계수는 상대 표준 편차(Relaative standard deviation, RSD)라고도 한다.
- 변동 계수는 측정 단위가 서로 다른 데이터의 산포도를 비교할 때 사용한다.
- 표준편차와 산술 평균 모두 단위가 있으나, 이 둘을 나눔으로써 단위가 사라지게 된다.
- 평균과 표준편차는 단위가 존재하며, 서로 다른 데이터끼리 그 흩어져있음을 비교하기 위해선 변동 계수를 만들어, 단위를 없애야만 서로 비교해볼 수 있다.
- 변동 계수가 클수록 상대적인 산포도가 크다고 할 수 있다.
3.1. 예시 및 파이썬 구현
- A반의 키는 평균 164cm, 표준편차는 12cm가 나왔다.
- A반의 몸무게는 평균 57 kg, 표준편차 10kg이 나왔다.
- 키와 몸무게는 서로 다른 변수이므로, 단위 역시 다르기 때문에 이들의 표준편차를 단순하게 비교해서는 안된다.
def CV(mean, std):
return std/mean# 키의 변동계수
>>> CV(164, 12)
0.07317073170731707
# 몸무게의 변동계수
>>> CV(57, 10)
0.17543859649122806- 위 결과를 보면, 몸무게의 변동 계수는 0.1754, 키의 변동 계수는 0.731로 몸무게의 변동 계수가 더 크므로, 몸무게가 키보다 산포도가 크다는 것을 알 수 있다.
- 변동 계수는 그 공식이 매우 단순하므로, 위처럼 평균과 표준편차를 출력하여 바로 구할 수도 있다.
def CV(data, column):
target_array = data[column].to_numpy()
return np.std(target_array)/np.mean(target_array)>>> CV(Rawdata, "키")
0.05189104256446505
>>> CV(Rawdata, "몸무게")
0.2196611158371381- 또는 위 함수처럼 numpy로 평균과 표준편차를 직접 생성하여, 구할 수도 있다.
728x90
반응형
'Python으로 하는 기초통계학 > 기본 개념' 카테고리의 다른 글
| 대푯값과 비대칭도, 왜도(Skewness), 첨도(Kutosis) (0) | 2021.03.11 |
|---|---|
| 산포도 - 편차: 분산 & 표준 편차 & 표준편차에 (n-1)을 나누는 이유 & 자유도 (0) | 2021.03.05 |
| 산포도(Dispersion) - 범위, 사분위간 범위, 사분위수와 상자 수염 그림 (0) | 2021.03.04 |
| 중심경향치(2) - 산술 평균, 기하 평균, 조화 평균, 모평균과 표본 평균이 같은 이유 (0) | 2021.03.03 |
| 중심경향치(1) - 최빈값, 중앙값 (0) | 2021.03.03 |