선형 회귀 모델 - 경사 하강법(Gradient descent, GD)
지난 포스트까지 정규방정식(Normal Equation)과 최소제곱법(Least Squares method)을 이용하여 선형 회귀(Linear Regression)의 모델 파라미터를 계산해보았다.
정규방정식이나 최소제곱법을 이용하여 모델 파라미터를 계산하는 경우, 공식이 꽤나 단순하고 단 한 번만 연산을 해도 된다는 장점이 있지만, 칼럼의 양이 2배 늘어나는 경우 정규방정식은 계산 시간이 최대 약 8배까지 증가하며, 최소제곱법은 계산 시간이 최대 4배까지 증가한다는 단점이 있다고 하였다.
때문에, 데이터의 피처(컬럼의 수)가 매우 많거나 데이터 자체가 큰 경우, 정규방정식이나 최소제곱법을 사용하여 선형 회귀의 모델 파라미터를 계산하는 것보다. 경사 하강법(Gradient descent)을 사용하여 계산하는 것이 보다 유리하다.
이번 포스트에서는 경사 하강법에 대해 알아보고, 경사하강법을 사용하여 선형 회귀 모형으로 학습을 해보도록 하겠다.
1. 경사 하강법이란?
- 앞서 우리는 선형 회귀 모델의 손실 함수인 MSE에 대해 알아보았다.
$$ MSE = \frac{1}{n}\sum_{i=1}^{n}(\hat{y_i} - y_i)^2 $$
- MSE에서 $\hat{y_i} = \theta x + b$이므로($\theta$: 계수, $x$: 실제 값, $b$: 절편), 학습을 통해 알고자 하는 미지수인 모델 파라미터 $\theta$는 1개의 최적해를 갖는 이차 함수 형태인 것을 알 수 있다.
- 때문에 손실 함수의 개형은 아래와 같다.

- 선형 회귀 모델을 비롯한 머신러닝 알고리즘에서 최고의 모델 파라미터를 찾는 방법은 손실 함수(Loss function)을 최소로 만드는 점 $\alpha$를 찾는 것이다.
- 정규방정식이나 최소제곱법은 우리가 찾고자 하는 $\alpha$를 한 번에 찾는 방법이고, 경사 하강법은 손실 함수의 랜덤 한 위치에서 기울기를 계산하고, 기울기가 0이 되는 방향으로 학습률(Learning rate)만큼 점진적으로 이동하여, 최적해 $alpha$를 찾는 방법이다.
- 위 과정은 전역 최적해(Global minimub)를 찾기 위해 반복 수행되며, 반복 수행된다는 의미는 다양한 랜덤한 위치에서 경사 하강법이 실시된다는 의미다.
- 보다 자세히 경사 하강법의 원리를 알고자 하는 경우, 이전 포스트인 "딥러닝-6.0. 최적화(1)-손실함수와 경사하강법"을 참고하기 바란다.
1.1 경사 하강법의 한계점
- 경사 하강법의 태생적 문제로 인해 다음과 같은 한계점이 존재한다.
- 데이터가 많아질수록 계산량 증가: 학습 데이터의 양이 늘어나는 경우, 계산량이 매우 커져 학습 속도가 느려진다.
- 지역 최소해(Local minimum) 문제: 실제 손실 함수의 형태는 위 그래프처럼 매끈하지 않고, 울퉁불퉁하기 때문에 실제로 찾아야 하는 전역 최적해(Global minimum)가 아닌 지역 최소해(Local minimum)를 찾을 수 있다.
- Plateau 문제: 평평한 지역(Plateau)에 들어가서, 학습이 더 이상 진행되지 못하는 문제
- Zigzag 문제: 찾아야 하는 해가 많아질수록 차원이 복잡해져, 제대로 해를 찾지 못하는 문제
- 위 내용에 대해 보다 자세히 알고자 하는 경우, 이전 포스트인 "딥러닝-6.1. 최적화(2)-경사하강법의 한계점"을 참고하기 바란다.
2. 경사 하강법의 공식 - 배치 경사 하강법(Batch Gradient Descent)
- 앞서 봤던 MSE 공식을 이번에는 벡터 형태로 가지고 와보자.
$$ MSE(X, h_{\theta}) = MSE(\theta) = \frac{1}{n}\sum_{i=1}^{n}(\theta^Tx^{(i)} - y^{(i)})^2 $$
- 위 식을 모델 파라미터 $\theta$에 대해 편미분 해보자.
$$\frac{\partial}{\partial \theta_j}MSE(\theta) = \frac{2}{n}\sum_{i=1}^{n}(\theta^T x^{(i)} - y^{(i)})x_{j}^{i}$$
- 위 편미분 결과에 대하여, 모든 모델 파라미터 $\theta_j$의 성분에 대한 편미분으로 구성된 열벡터로 만들어보고, 이를 행렬식으로 바꿔보자.
$$\bigtriangledown_{\theta} MSE(\theta) =
\begin{pmatrix} \frac{\partial}{\partial \theta_0}MSE(\theta)
\\ \frac{\partial}{\partial \theta_1}MSE(\theta)
\\ \vdots
\\ \frac{\partial}{\partial \theta_0}MSE(\theta)
\end{pmatrix} = \frac{2}{m}X^T(X\theta - y)$$
- 경사 하강법 공식은 다음과 같다.
$$x_{i+1} = x_i - \eta \bigtriangledown f(x_i)$$
- 위 경사 하강법 공식에서 손실함수 $\bigtriangledown f(x_i)$의 위치에, 위에서 구한 $MSE$의 편미분 행렬식인 $\bigtriangledown_{\theta} MSE(\theta)$을 넣어주고, 미지수$x$도 선형 회귀의 모델 파라미터인 $\theta$로 바꿔 선형 회귀 모델에 대한 경사 하강법 공식으로 만들어주자.
$$\theta_{i+1} = \theta_i - \eta \bigtriangledown MSE(\theta) = \theta_i - \frac{2}{m} \eta X^T(X\theta - y)$$
- 위 공식은 매 경사 하강법 스텝에서 전체 훈련 세트 $X$에 대해 계산한다. 이를 배치 경사 하강법(Batch gradient descent)라 하며, 매 스텝에서 훈련 데이터 전체를 대상으로 최적해를 찾기 때문에 계산 시간도 길고, 소모되는 컴퓨터 자원의 양도 많다.
- 때문에 매우 큰 데이터를 대상으로 할 때는 위 공식인 배치 경사 하강법을 사용하지 않는 것이 좋으며, 무작위 샘플 데이터 셋을 추출해, 그 샘플에 대해서만 경사 하강법을 실시하는 확률적 경사 하강법(Stochastic Gradient Descent, SGD)을 실시하는 것이 좋다.
- 그러나, 경사 하강법은 특성 수에 민감하지 않기 때문에, 특성 수가 매우 많은 경우, 정규방정식이나 특잇값 분해(SVD)를 이용한 최소제곱법보다 경사 하강법을 사용하여 학습하는 것이 좋다.
- 경사 하강법 공식의 $\eta$는 학습률(Learning rate)라 하며, 에타라고 발음한다. 경사 하강법은 현재(n)의 파라미터 $\theta$에서 MSE의 편미분 벡터에 학습률을 곱한 수치만큼 아래 방향으로 이동한다.
3. 넘파이 코드를 이용해서 배치 경사 하강법을 구현해보자.
- 위에서 행렬식으로 만든 경사 하강법 함수는 다음과 같다.
$$\theta_{i+1} = \theta_i - \frac{2}{m} \eta X^T(X\theta - y)$$
- 경사 하강법은 최적의 모델 파라미터를 찾기 위해 전체 데이터에 대하여 m번 반복하여 계산된다.
- 이 반복되는 것을 학습 단위라고 하며, Epoch(에포크), Batch size(배치 사이즈), Iteration(이터레이션)에 대한 기본 개념을 알아야 한다.
- Epochs: 전체 데이터를 학습 시키는 횟수
- Batch size: 연산 한 번에 들어가는 데이터의 크기
- Iteration: 1 epoch를 마치는데 필요한 모델 파라미터 업데이터의 횟수
- 보다 자세한 내용은 다음 포스트 "딥러닝-6.2. 최적화(3)-학습 단위(Epoch, Batch size, Iteration)"을 참고하기 바란다.
- 이번에는 1 epoch에서 모델 파라미터를 m번 갱신(Iteration)해보도록 하겠다.
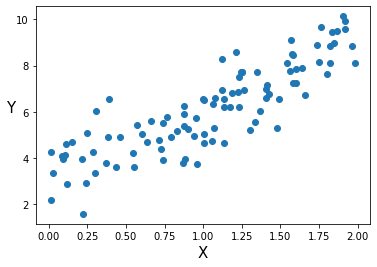
3.1. 사용할 데이터
- 데이터는 이전 포스트에서 사용했던 컬럼이 1개인 데이터를 사용해보겠다.
import numpy as np
import matplotlib.pyplot as pltnp.random.seed(1234)
def f(x):
return 3 * x + 4
X = 2 * np.random.rand(100, 1)
Y = f(X) + np.random.randn(100, 1)
# 상수항을 위해 모든 원소가 1인 컬럼을 추가함
X_b = np.c_[X, np.ones((100, 1))]- 생성한 데이터를 sklearn 라이브러리의 LinearRegression 모델을 사용하여, 학습시켜보겠다.
- sklearn의 LinearRegression에 학습시킬 때는 상수항을 위해 모든 원소가 1인 컬럼을 추가하지 않아도 된다.
# sklearn 라이브러리의 선형 회귀 모형
from sklearn.linear_model import LinearRegression
LR_model = LinearRegression()
LR_model.fit(X, Y)>>> LR_model.coef_, LR_model.intercept_
(array([[2.94132381]]), array([4.07630632]))- 숨겨진 패턴인 함수 $f(x) = 3x + 4$의 계수 3과 상수 4에 근사한 결과가 나왔다.
3.2. 배치 경사 하강법 코드
def Batch_GD(x, y, eta=0.01, iteration_N=1000):
# 초기 무작위 파라미터
theta = np.random.randn(x.shape[1], 1)
for iteration in range(iteration_N):
# MSE의 편미분 벡터
gradients = (2/x.shape[0])* x.T.dot(x.dot(theta) - y)
theta = theta - eta * gradients
return theta>>> Batch_GD(X_b, Y, 0.01, 1000)
array([[3.02789289],
[3.97237607]])
- 학습률 eta나 파라미터 갱신 횟수 iteration_N과 같은 분석가가 직접 설정하는 파라미터를 머신러닝에서는 하이퍼 파라미터라고 한다.
- 학습률이 크면 클수록 빠르게 최적해에 수렴하나, 너무 크게 이동하므로 전역 최적해에 수렴하지 못할 수 있다.
- 학습률을 보다 크게 학습시켜보자.
>>> Batch_GD(X_b, Y, 0.1, 1000)
array([[2.94132381],
[4.07630632]])- 학습률이 0.1로 10배나 커지자, 보다 빠르게 수렴하여 최소제곱법(LSM)을 사용하여 회귀 모델의 최적의 파라미터를 계산하는 sklearn의 LinearRegression과 같은 결과가 나왔다.
4. 학습률과 Iteration에 따른 수렴 속도의 차이 시각화
- 위에서 만든 Batch_GD 함수를 약간 수정하여, 갱신된 파라미터에 대한 예측값을 plot으로 시각화하는 함수를 만들어보자.
# 전체 시각화
def draw_eta(x, y, eta_, iteration_N_):
plt.scatter(x, y)
# 상수항을 위한 모든 원소가 1인 컬럼 추가
x_b = np.c_[x, np.ones((X.shape[0], 1))]
Batch_GD_Visual(x_b, y, eta=eta_, iteration_N=iteration_N_)
# 제목
plt.xlabel("X", fontsize = 15)
plt.ylabel("Y", fontsize = 15, rotation = 0)
plt.title(f"$\eta$={eta_}", fontsize = 20, pad=15)
plt.xlim(0, 2)
plt.ylim(0, 15)
plt.show()
# 갱신되는 theta에 따른 경사 하강법 시각화
def Batch_GD_Visual(x, y, eta=0.01, iteration_N=1000):
# 초기 무작위 파라미터
theta = np.random.randn(x.shape[1], 1)
for iteration in range(iteration_N):
# MSE의 편미분 벡터
gradients = (2/x.shape[0])* x.T.dot(x.dot(theta) - y)
theta = theta - eta * gradients
# 경사 하강법을 통해 바뀐 theta로 예측한 값
new_Y = np.array([[0,1],[2,1]]).dot(theta)
plt.plot([0,2], new_Y, c = "r", alpha = 0.2)
return theta- draw_eta는 시각화 코드를 정리해놓은 함수다.
- Batch_GD_Visual은 갱신되는 $\theta$에 따른 경사 하강법을 시각화하는 함수로, 옅은 빨간색 선을 그린다.
4.1. iteration은 50이고, 학습률이 변하는 경우
- iteration 1000은 꽤 큰 값이므로, 작은 50으로 설정해놓고 학습률만 바꿔보자.
- 학습률이 0.01인 경우
eta_ = 0.01
iteration_N_ = 50
draw_eta(X, Y, eta_, iteration_N_)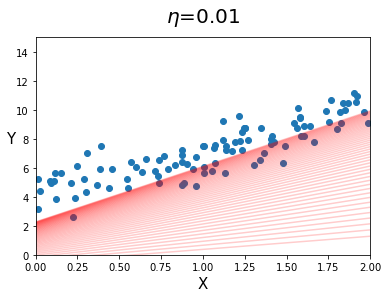
- 학습률이 0.1인 경우
eta_ = 0.1
iteration_N_ = 50
draw_eta(X, Y, eta_, iteration_N_)
- 학습률이 0.5인 경우
eta_ = 0.5
iteration_N_ = 50
draw_eta(X, Y, eta_, iteration_N_)
- 위 결과를 보면, 학습률이 커지면 커질수록 빠르게 최적해를 찾아가는 것을 볼 수 있지만, $\eta=0.5$ 같이 지나치게 큰 경우, 모델 파라미터가 큰 폭으로 요동치는 것을 볼 수 있다.
- 위에서 볼 수 있듯, 데이터에 맞는 적절한 학습률을 찾는 것은 매우 중요하다.
4.2. 학습률은 0.01이고, iteration이 변하는 경우
- 학습률을 최적해에 비교적 늦게 수렴하는 0.01로 잡고, 파라미터 갱신 횟수인 iteration만 바꿔보자.
(꽤 많은 머신러닝 알고리즘에서 Learning rate의 기본값을 0.01로 잡아놓는다.) - iteration이 10인 경우
eta_ = 0.01
iteration_N_ = 10
draw_eta(X, Y, eta_, iteration_N_)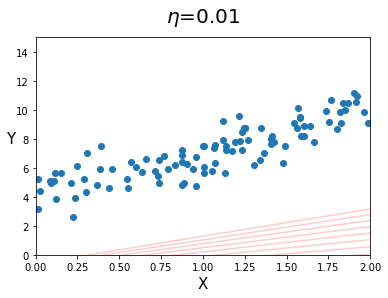
- iteration이 30인 경우
eta_ = 0.01
iteration_N_ = 30
draw_eta(X, Y, eta_, iteration_N_)
- iteration이 100인 경우
eta_ = 0.01
iteration_N_ = 100
draw_eta(X, Y, eta_, iteration_N_)
- 위 결과를 보면, 파라미터 갱신량도 필요치보다 작은 경우, 최적해를 찾기 전에 경사 하강이 끝나버리고, 필요치 보다 큰 경우, 최적해를 찾고 파라미터가 더 이상 변하지 않는 시간 낭비가 발생하는 것을 볼 수 있다.
- 이에 대한 해결책으로는, iteration을 애초에 크게 잡은 후, 경사 하강법 알고리즘에 규제를 추가하여, 모델 파라미터의 변화량이 허용오차(tolerance) $\varepsilon$보다 작아지면 최적해에 도달한 것으로 판단하고 모델 파라미터 갱신을 중지시키는 것이다.
[참고 서적]

이번 포스트에서는 배치 경사 하강법을 이용하여 선형 회귀 모형을 만들어보았다. 배치 경사 하강법은 데이터가 지나치게 큰 경우 계산 시간이 지나치게 오래 걸리는 정규방정식이나 최소제곱법보다 빠르게 최적해를 찾을 수 있다.
그러나, 학습률, 파라미터 갱신 횟수(iteration)과 같은 하이퍼 파라미터를 제대로 잡지 않는다면, 학습 시간이 필요보다 길어지거나, 최적해에 수렴하지 못할 수 있으므로, 최적의 하이퍼 파라미터를 찾을 수 있어야 한다.
배치 경사 하강법은 모든 데이터에 대한 편미분 벡터를 계산하게 되므로, 데이터의 크기가 이보다 더 커지는 경우, 학습 시간이 더 길어질 수 있다. 다음 포스트에서는 이 문제를 해결한 확률적 경사 하강법에 대해 알아보도록 하겠다.
'Machine Learning > ML_Algorithm' 카테고리의 다른 글
| ML알고리즘-1.1. 선형 회귀의 구현 - 정규방정식과 최소제곱법 (0) | 2021.03.21 |
|---|---|
| ML알고리즘-1.0. 선형 회귀(Linear Regression)와 정규방정식 (0) | 2021.03.20 |