ML알고리즘-1.1. 선형 회귀의 구현 - 정규방정식과 최소제곱법

선형 회귀의 구현 - 정규방정식과 최소제곱법

 지난 포스트에서 머신러닝에서 선형 회귀 모델의 기본적인 원리에 대해 알아보았다. 이번 포스트는 정규방정식을 넘파이 함수로 구현해보고, 정규방정식으로 찾아낸 최적의 모델 파라미터를 이용해서 새로운 데이터에 대해 예측을 해보자.

 

 

 

 

1. 선형성을 갖는 무작위 데이터를 만들어보자.

• 임의의 선형 데이터를 만들어 정규방정식에 넣어보도록 하자.

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(1234)

def f(x):
    return 3 * x + 4

X = 2 * np.random.rand(100, 1)
Y = f(X) + np.random.randn(100, 1)

• np.random.rand(shape): 0~1 사이의 표준 정규 분포 난수를 shape의 형태대로 생성
• np.random.randn(shape): 평균 0, 표준편차 1의 가우시안 표준 정규 분포 난수를 shape의 형태대로 생성
• 0에서 1 사이의 난수 X에 2를 곱하여, 값의 범위를 더 넓게 하였다.
• 숨겨진 패턴은 함수 $f(x) = 3x + 4$이며, $f(x)$에 $N(0,1)$인 가우시안 표준 정규 분포를 더해 노이즈를 주었다.

plt.scatter(X, Y)

plt.xlabel("X", fontsize=15)
plt.ylabel("Y", rotation=0, fontsize=15)
plt.show()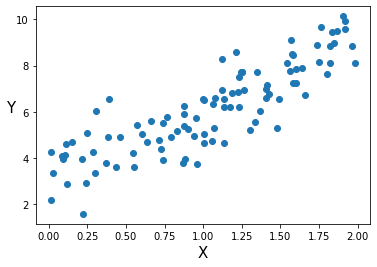

 

 

 

 

 

2. 넘파이 코드를 사용해서 정규방정식을 구현해보자.

• 정규방정식 함수는 다음과 같다.

$$\hat{\theta} = (X^TX)^{-1}X^Ty$$

• 위 정규방정식 함수를 넘파이 라이브러리의 함수를 사용해서 함수로 만들어보자.

# 정규방정식
def NormalEquation(X, Y):
    
    return np.linalg.inv(np.dot(X.T, X)).dot(X.T).dot(Y)

• np.linalg.inv(): 역행렬
• np.dot(mat1, mat2): 행렬 mat1과 mat2의 행렬 곱 연산을 한다.
• mat1.dot(mat2): 행렬 mat1과 mat2의 행렬 곱 연산을 한다.

 

2.1. 배열 X와 Y를 넣어보자

>>> NormalEquation(X, Y)
array([[6.00122666]])

• 위 데이터에서 숨겨진 패턴인 함수 $f(x)$는 $f(x) = 3x + 4$이므로, 3과 4가 출력되어야 하지만, 원소가 단 하나만 출력되었다.
• 이는 함수 $f(x)$에 들어가는 배열 X에 절편에 대한 칼럼이 반영되지 않았기 때문이다.
• 절편 4는 4*1이므로, 배열 X에 모든 원소가 1인 칼럼을 하나 추가해주고, 정규방정식을 수행해보도록 하자.

 

2.2. 절편에 대한 칼럼이 반영된 배열 X와 Y를 넣어보자.

# 절편에 대한 1로 구성된 벡터를 추가함.
>>> X_b = np.c_[X, np.ones((100, 1))]

# 정규방정식을 통해 최적의 계수를 찾아냄
>>> NormalEquation(X_b, Y)
array([[2.94132381],
       [4.07630632]])

• np.c_[array1, array2]: array1과 array2를 컬럼 방향으로 붙인다(오른쪽에 붙인다)
• 위 결과를 보면, 숨겨진 패턴인 함수 $f(x) = 3x + 4$의 계수인 3과 4와 아주 가까운 값이 도출된 것을 볼 수 있다.
• 숨겨진 패턴의 계수 3과 4가 나오지 않은 이유는, 의도적으로 노이즈를 주었기 때문이며, 그 노이즈를 반영하였을 때, 숨겨진 패턴에 가장 가까운 모델 파라미터가 출력된 것이다.

 

2.3. 변수 $x$가 2개인 데이터에 대하여 정규방정식을 이용해 최적해를 구해보자.

• 이번에는 숨겨진 패턴이 $h(x) = 3x_1 + 4x_2 + 5$인 함수에 대하여 구해보자.
• 변수  $x$가 2개이므로, 컬럼의 수는 2개가 되어야 한다.

X1 = 2 * np.random.rand(100, 2)

def h(x):
    x1 = x[:,0]
    x2 = x[:,1]
    
    result = 3 * x1 + 4 * x2 + 5
    
    return result.reshape(100, 1)

Y1 = h(X1) + np.random.randn(100, 1)

# 절편을 위해 모든 원소가 1인 컬럼 추가
X1_b = np.c_[X1, np.ones((100, 1))]

>>> NormalEquation(X1_b, Y1)
array([[2.93017703],
       [4.19897028],
       [4.90893137]])

• 각 계수의 값이 3, 4, 5에 근사하게 나왔으나, 실제 값과 어느 정도 거리가 있다.
• 데이터의 양이 늘어날수록 실제 계수에 더 가까워진다.

X2 = 2 * np.random.rand(10000, 2)

def h(x):
    x1 = x[:,0]
    x2 = x[:,1]
    
    result = 3 * x1 + 4 * x2 + 5
    
    return result.reshape(10000, 1)

Y2 = h(X2) + np.random.randn(10000, 1)
X2_b = np.c_[X2, np.ones((10000, 1))]

>>> NormalEquation(X2_b, Y2)
array([[2.98528199],
       [4.01290386],
       [5.00091078]])

 

 

 

 

 

3. 찾아낸 모델 파라미터를 이용해서 예측을 해보자.

• 정규방정식을 통해 계산해 낸 선형 회귀 모델의 파라미터 $\hat{\theta}$를 사용해서 새로운 데이터가 들어갔을 때, 그 결과를 예측해보자.

def predict_linear_R(X, theta):
    
    R_n = X.shape[0]
    
    try:
        C_n = X.shape[1]
    except:
        C_n = 1
    
    X_Reshape = X.reshape(R_n, C_n)
    X_concat_1 = np.c_[X_Reshape, np.ones((R_n,1))]
    
    return X_concat_1.dot(theta)

 

3.1. 독립변수가 1개인 경우

• 처음 만들었던 칼럼이 1개 있는 데이터의 최적 모델 파라미터에 대하여, 새로운 데이터를 넣어 새로운 데이터에 대한 예측 값을 뽑아보자.
• 새로운 데이터는 [0, 1, 2]로 구성된 벡터이다.

def f(x):
    return 3 * x + 4

X = 2 * np.random.rand(100, 1)
Y = f(X) + np.random.randn(100, 1)

X_b = np.c_[X, np.ones((100, 1))]
best_theta = NormalEquation(X_b, Y)

>>> best_theta
array([[2.94132381],
       [4.07630632]])

# 새로운 데이터
>>> new_X = np.array([0, 1, 2]).reshape((3,1))

# 새로운 데이터를 학습된 선형 회귀 모형에 넣어 예측된 결과
>>> pred_LR = predict_linear_R(new_X, best_theta)
>>> pred_LR
array([[4.07630632],
       [7.01763013],
       [9.95895394]])

• 기존에 그린 산점도 위에 예측된 결과를 그려보자.

plt.scatter(X, Y, label="real")
plt.plot(new_X, pred_LR.reshape(new_X.shape), color = "red", label="predict")

plt.xlabel("X", fontsize=15)
plt.ylabel("Y", rotation=0, fontsize=15)
plt.legend(loc="lower right")
plt.show()

 

3.2. 독립변수가 2개인 경우

X1 = 2 * np.random.rand(100, 2)

def h(x):
    x1 = x[:,0]
    x2 = x[:,1]
    
    result = 3 * x1 + 4 * x2 + 5
    
    return result.reshape(100, 1)

Y1 = h(X1) + np.random.randn(100, 1)
X1_b = np.c_[X1, np.ones((100, 1))]
best_theta1 = NormalEquation(X1_b, Y1)

>>> best_theta1
array([[2.93017703],
       [4.19897028],
       [4.90893137]])

>>> new_X1 = np.array([[0, 1],[0.5, 1.5],[1, 2]])

>>> predict_linear_R(new_X1, best_theta1)
array([[ 9.10790166],
       [12.67247531],
       [16.23704897]])

• 독립변수가 2개 이상인 경우, 독립 변수의 축 2개 + 종속변수의 축 1개로 3개 이상의 축이 생겨, 시각화가 어려워진다. 그러므로, 시각화는 생략하도록 하겠다.
• 최적의 모델 파라미터만 찾아내면, 쉽게 회귀 모델을 사용해서, 예측값을 찾아낼 수 있다.

 

 

 

 

 

4. 사이킷런을 사용해서 선형 회귀를 실시해보자.

• 사이킷런을 사용하면, 더 쉽게 위 과정을 진행할 수 있다.

from sklearn.linear_model import LinearRegression

lin_R = LinearRegression()

• 사용하고자 하는 모델인 선형 회귀 모형을 객체로 만들었다.
• 앞서 만든 데이터 X와 Y를 사용하여, 최적의 모델 파라미터를 찾아보자.

# 선형 회귀 모형 학습
>>> lin_R.fit(X, Y)

# 계수와 절편 출력
>>> lin_R.coef_, lin_R.intercept_
(array([[2.94132381]]), array([4.07630632]))

# Numpy로 만든 정규방정식의 결과
>>> best_theta
array([[2.94132381],
       [4.07630632]])

• 모델.fit(array1, array2): 원하는 모델을 학습시킨다. array1은 훈련 데이터(Test data), array2는 레이블 데이터(Label data)다.
• 선형회귀모델.intercept_, 선형회귀모델.coef_: sklearn을 사용하여, 선형 회귀 모형을 학습시키면, 계수와 절편의 값이 따로 출력된다. coef_는 계수이며, intercept_는 절편이다.
• sklearn을 사용하여 계산된 결과와 numpy를 사용하여 만든 정규방정식의 결과가 동일한 것을 볼 수 있다.
• 이번에는 학습된 모델 파라미터를 사용하여, 새로운 데이터가 들어갔을 때의 결과를 예측해보자.

# sklearn을 이용하여 예측한 결과
>>> lin_R.predict(new_X)
array([[4.07630632],
       [7.01763013],
       [9.95895394]])
       
# numpy 라이브러리를 사용하여 예측한 결과
>>> predict_linear_R(new_X, best_theta)
array([[4.07630632],
       [7.01763013],
       [9.95895394]])

• 모델.predict(array): array에 모델 파라미터를 계산하여, 예측된 결과를 출력한다.

 

 

 

 

 

5. 정규방정식의 한계점

5.1. 의사역행렬(Pseudoinvese matrix)과 최소제곱법(LSM)

• 앞서 우리가 학습하였던 정규방정식에는 큰 한계점이 존재한다.
• 정규방정식 공식 $\hat{\theta} = (X^TX)^{-1}X^Ty$에는 역행렬이 포함되어 있는데, 역행렬은 항상 존재하는 것이 아니기 때문에 역행렬이 존재하지 않는다면, 정규방정식 공식은 작동하지 않을 수 있다.
• 때문에 등장하는 것이 무어-펜로즈 역행렬(Moore-Penrose pseudoinverse matrix)이라고도 불리는 의사역행렬(Pseudoinverse matrix)을 사용하여 다음과 같은 공식으로 최적의 모델 파라미터를 찾아내게 된다.

$$ \hat{\theta} = X^{+}y$$

• 의사역행렬은 특잇값 분해(Singular value decomposition, SVD)라는 표준 행렬 분해 기법을 통해 계산되며, 의사역행렬은 역행렬이 없는 행렬에 대해서도 계산을 할 수 있기 때문에 정규방정식의 한계점을 해결할 수 있으며, 계산 속도 또한 빠르다.
• 선형 회귀 모델의 회귀 계수(모델 파라미터)를 추정할 때, 가장 많이 사용되는 기법인 최소제곱법(Least squares method, LSM)은 의사역행렬을 사용하여 해를 구하므로, sklearn의 선형 회귀 모델은 정규방정식이 아닌 최소제곱법을 기반으로 계산한다.

>>> np.linalg.lstsq(X_b, Y, rcond=1e-6)
(array([[2.94132381],
        [4.07630632]]),
 array([92.72583695]),
 2,
 array([14.98211623,  3.69398772]))

• np.linalg.lstsq(array1, array2): array1, array2의 최소제곱해를 선형 행렬 방정식으로 반환한다.
• 위 함수를 사용하면 총 4개의 결과가 반환되는데, 여기서 맨 처음에 반환된 결과인 최소제곱해만 신경 쓰면 된다.

# 최소제곱해
>>> np.linalg.lstsq(X_b, Y, rcond=1e-6)[0]
array([[2.94132381],
       [4.07630632]])
       
       
# Numpy로 만든 정규방정식의 결과
>>> best_theta
array([[2.94132381],
       [4.07630632]])

• 보시다시피 최소제곱법을 사용해서 구하는 최소제곱해와 정규방정식의 결과는 동일한 것을 알 수 있다.
• 그러나, 최소제곱법은 의사역행렬을 통해 계산되기 때문에 역행렬이 존재하지 않는 대상에 대해서도 계산이 가능하다.

 

5.2. 정규방정식의 계산복잡도

• 정규방정식은 역행렬 계산, 행렬 곱 등 다양한 행렬 연산이 들어가기 때문에 계산 복잡도(Computation complexity)가 매우 크다.
• 정규방정식을 사용할 때, 특성의 수가 2배 늘어나면, 계산 시간이 약 5.3배에서 8배로 증가하며, 특잇값 분해(SVD)를 통해 의사역행렬을 구한다 할지라도 특성의 수가 2배 늘어나는 경우, 계산 시간이 약 4배 증가하게 된다.
• 즉, 칼럼의 수가 늘어나면 늘어날수록 계산 시간이 기하급수적으로 늘어나기 때문에, 칼럼이 많은 데이터를 정규방정식이나 최소제곱법으로 구하는 경우, 시간이 매우 오래 걸리게 된다.
  (행의 수가 늘어나는 경우, 늘어난 샘플 수만큼 선형적으로 소모 시간이 증가하기 때문에 행의 수는 큰 영향을 안 준다.)
• 만약, 칼럼의 양이나 데이터 자체가 매우 많은 경우, 계산량이 지나치게 많아, 메모리를 넘어설 수 있기 때문에, 정규방정식이나 최소제곱법을 사용하지 못할 수도 있다.

 

 

[참고]

numpy.org/doc/stable/reference/generated/numpy.linalg.lstsq.html

numpy.linalg.lstsq — NumPy v1.20 Manual

blog.daum.net/jungjin1980/77

특이값 분해

 

 

 

 지금까지 정규방정식과 정규방정식의 한계점을 보완한 최소제곱법에 대해 간략히 알아보고, 코드화해 보았다. 최소제곱법은 선형 회귀 모형을 다룰 때, 굉장히 심도 있게 공부해야 하는 부분이므로, 기초 통계학 부분에서 보다 자세히 다루도록 하겠다.

 다음 포스트에서는 선형 회귀 모형을 정규방정식이나 최소제곱법이 아닌, 경사하강법을 사용해서 구하는 방법에 대해 알아보도록 하겠다.