만년필잉크의 데이터 분석 지식 저장소

 이전 포스트에서는 학습 단위에 대한 단어인 에포크(Epoch), 배치 크기(Batch size), 이터레이션(Iteration)에 대해 알아보았다. 이번 포스트에서 알아볼 확률적 경사 하강법(SGD)의 키는 배치 크기와 랜덤 추출이다.

 경사 하강법에 다른 식을 붙이지 않고 바로 사용하는 방법은 크게 두 가지인 배치 경사 하강법(BGD)과 확률적 경사 하강법(SGD)이 있는데, 이 둘은 손실 함수의 기울기 계산에 사용되는 데이터 셋의 규모만 제외하고 같다.

 중요한 것은 손실 함수의 경사를 구하는 대상이다!

1. 배치 경사 하강법(Batch Gradient Descent, BGD)

• 배치 경사 하강법(BGD)은 경사 하강법의 손실 함수의 기울기 계산에 전체 학습 데이터셋의 크기와 동일하게 잡는 방법이다.
• 즉, 경사 하강법 대상이 배치 크기와 동일하다는 것이다.
• 데이터셋 모두를 대상으로 하다 보니 파라미터가 한번 이동할 때마다, 계산해야 할 값이 지나치게 많으므로, 계산 시간도 엄청 길어지고, 소모되는 메모리도 엄청나다.
• mini batch 안 모든 데이터를 대상으로 경사 하강법을 실시하므로, 안정적으로 수렴한다.

• 안정적으로 수렴하므로, 수렴까지 발생하는 총 파라미터 업데이트 수는 매우 적다.
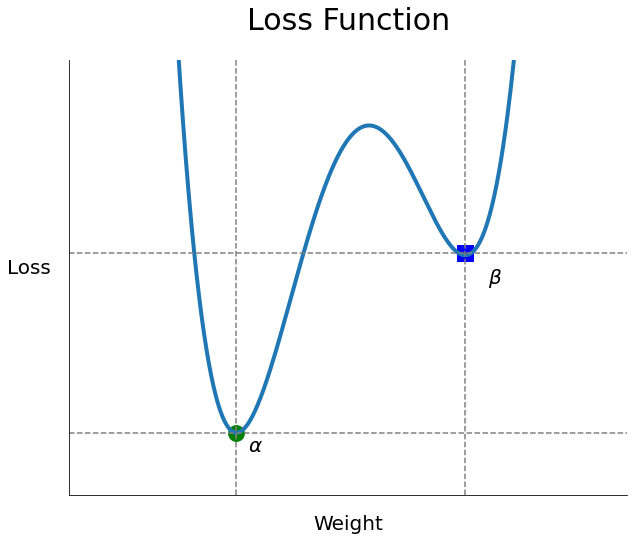
• 안정적으로 수렴하는 것은 좋으나, 안정적으로 움직이기 때문에 지역 최소해(Local Minimum)에 빠지더라도 안정적으로 움직이므로 빠져나오기 힘들다. 즉, Local Optima(minimum) 문제가 발생할 가능성이 높다.
• 학습 데이터셋이 커지면 커질수록 시간과 리소스 소모가 지나치게 크다.

2. 확률적 경사 하강법(Stochastic Gradient Descent, SGD)

• 전체 훈련 데이터셋을 대상으로 학습하는 것은 한정된 리소스를 가지고 있는 우리의 분석 환경에서 매우 비효율적이며, 파라미터 업데이트 수가 적다는 것은 랜덤 하게 뽑힌 시작 위치의 가중치 수도 적으므로, Local minimum 현상이 발생할 확률도 높다는 것이다.
• 그래서 나온 방법이 학습 데이터셋에서 무작위로 한 개의 샘플 데이터 셋을 추출하고, 그 샘플에 대해서만 기울기를 계산하는 것이다.
• 샘플 데이터 셋에 대해서만 경사(Gradient)를 계산하므로, 매 반복에서 다뤄야 할 데이터 수가 매우 적어, 학습 속도가 매우 빠르다.
• 하나의 샘플만 대상으로 경사를 계산하므로, 메모리 소모량이 매우 낮으며, 매우 큰 훈련 데이터 셋이라 할지라도 학습 가능하다.
• 그러나, 무작위로 추출된 샘플에 대해서 경사를 구하므로, 배치 경사 하강법보다 훨씬 불안정하게 움직인다.

• 손실 함수가 최솟값에 다다를 때까지 위아래로 요동치며 움직이다 보니, 학습이 진행되다 보면, 최적해에 매우 근접하게 움직이긴 하겠으나, 최적해(Global minimum)에 정확히 도달하지 못할 가능성이 있다.
• 그러나, 이렇게 요동치며 움직이므로, 지역 최솟값(Local minimum)에 빠진 다할지라도, 지역 최솟값에서 쉽게 빠져나올 수 있으며, 그로 인해 전역 최솟값(Global minimum)을 찾을 가능성이 BGD에 비해 더 높다.
• 즉, 확률적 경사 하강법(SGD)은 속도가 매우 빠르고 메모리를 적게 먹는다는 장점이 있으나, 경사를 구할 때, 무작위성을 띄므로 지역 최솟값에서 탈출하기 쉬우나, 전역 최솟값에 다다르기 힘들다는 단점을 가지고 있다.
• 이 문제를 해결하기 미니 배치 경사 하강법(mini-Batch gradient descent)이 등장하였다.

학습률 스케줄(Learning rate schedule)

• 전역 최솟값에 도달하기 어렵다는 문제를 해결하기 위한 방법으로, 학습률을 천천히 줄여 전역 최솟값에 다다르게 하는 방법이 있다.
• 학습률은 작아질수록 이동하는 양이 줄어들기 때문에 전역 최솟값에 안정적으로 수렴할 수 있다.
• 만약 학습률이 너무 급격하게 감소하면, Local Optima 문제나 Plateau 현상이 발생할 가능성이 높아진다.
• 그렇다고 학습률을 너무 천천히 줄이면 최적해 주변을 맴돌 수 있다.

3. 미니 배치 경사 하강법(mini-Batch gradient descent)

• 앞서 이야기한 배치 경사 하강법(BGD)나 확률적 경사 하강법(SGD)은 모두 배치 크기가 학습 데이터 셋 크기와 동일하였으나, 미니 배치 경사 하강법은 배치 크기를 줄이고, 확률적 경사 하강법을 사용하는 기법이다.
• 예를 들어, 학습 데이터가 1000개고, batch size를 100으로 잡았다고 할 때, 총 10개의 mini batch가 나오게 된다. 이 mini batch 하나당 한 번씩 SGD를 진행하므로, 1 epoch당 총 10번의 SGD를 진행한다고 할 수 있다.
• 일반적으로 우리가 부르는 확률적 경사 하강법(SGD)은 실제론 미니 배치 경사 하강법(mini-BGD)이므로, 지금까지 학습했던 차이들은 기억하되, 앞으로 SGD를 말하면, 미니 배치 경사 하강법을 떠올리면 된다.

• 미니 배치 경사 하강법은 앞서 이야기했던, 전체 데이터셋을 대상으로 한 SGD보다 파라미터 공간에서 Shooting이 줄어들게 되는데, 이는 한 미니 배치의 손실 값 평균에 대해 경사 하강을 진행하기 때문이다.
• 그로 인해, 최적해에 더 가까이 도달할 수 있으나, Local optima 현상이 발생할 수 있다. 그러나, 앞서 말했듯 Local optima 문제는 무수히 많은 임의의 파라미터로부터 시작되면, 해결되는 문제이며, 학습 속도가 빠른 SGD의 장점을 사용하여, 학습량을 늘리면 해결되는 문제다.
• 배치 크기는 총 학습 데이터셋의 크기를 배치 크기로 나눴을 때, 딱 떨어지는 크기로 하는 것이 좋다.
• 만약, 1050개의 데이터에 대하여 100개로 배치 크기를 나누면, 마지막 50개 데이터셋에 대해 과도한 평가를 할 수 있기 때문이다.
• 그러나, 만약 배치 크기로 나누기 애매한 경우라면, 예를 들어 총 학습 데이터 셋이 1,000,050개가 있고, 배치 크기를 1,000개로 나누고 싶은 경우라면, 나머지인 50개는 버리도록 하자(물론 완전 무작위 하게 50개를 선택해서 버려야 한다.).

  지금까지 확률적 경사 하강법(SGD)에 대해 알아보았다. 본래의 SGD는 "배치 크기 = 학습 데이터 셋 크기"이지만, 일반적으로 통용되는 SGD는 "배치 크기 < 학습 데이터 셋 크기"인 미니 배치를 만들어 학습시키는 미니 배치 경사 하강법이다. 

 경사 하강법의 파이썬 코드화는 경사 하강법 함수 자체는 단순하지만, 학습에서 발생하는 모든 알고리즘이 복합적으로 작동하므로, 코드화시키는 것은 시간 낭비로 판단된다. Optimizer 파트부턴 그 개념과 특징을 이해하고, 텐서플로우로 학습을 해보도록 하자.

 다음 포스트에서는 경사 하강법의 한계점을 보완하기 위한 시도 중 하나인 모멘텀(Momentum)에 대해 학습해보도록 하겠다.

 지난 포스트에서는 기계학습에서 사용되는 최적화 알고리즘인 경사 하강법에 대하여 살펴보았다. 이번 포스트에서는 경사 하강법의 한계점에 대해 학습해보도록 하겠다.

경사 하강법의 한계점

• 앞서 손실함수를 기반으로 경사 하강법의 개형을 그려보았으나, 실제로는 저렇게 깔끔한 이차 함수 형태를 그리지 않는다.
• 퍼셉트론의 공식이 활성화 함수를 타게 되면, 손실 함수의 모습은 거시적인 관점에서 봤을 때는 최적해를 1개 가진 이차 함수의 형태를 그리긴 하지만, 그 모습이 울퉁불퉁해져 최적해에 수렴하기 어려워진다.
• 이번 포스트에서는 경사하강법의 한계점에 대해 하나하나 짚고 넘어가 보도록 하겠다.

1. 데이터가 많아질수록 계산량 증가

• 앞서, 경사하강법(Gradient Descent)은 신경망에서 출력되는 예측값(Predict)과 실제값(Label)의 차이인 손실 함수(Loss Function)의 값을 최소화하는 것이 목적이다.
• 그러나, 학습용 데이터 셋이 많아진다면, 당연히 계산량도 무지막지하게 많아지게 되는데, 그로 인해 학습 속도가 매우 느려지게 된다.
• 기계학습에는 아주 거대한 빅데이터가 사용되게 되는데, 이러한 퍼포먼스 문제는 결코 무시할 수 없는 문제다.

2. Local minimum(Optima) 문제

• 앞서 그린 대략적인 손실함수의 개형은 굉장히 매끈하였으나, 활성화 함수로 인해 그 모양이 울퉁불퉁해지게 되고, 그로 인해 최적해에 수렴하지 못할 수 있다.
• 아래 그래프를 보도록 하자.

• 실제 손실함수의 모양은 위 그래프보다 울퉁불퉁한 정도가 심하나 이해를 돕기 위해 일부분만 가져와봤다.
• 위 그래프에서 $\alpha$를 전역 최소해(Global minimum), $\beta$를 지역 최소해(Local minimum)라 한다.

• 경사 하강법의 목적은 손실 함수에서 랜덤 하게 선택한 가중치를 미분하여 나온 결과를 힌트로 해서, 최적해를 찾아가는 것인데, 위 그래프처럼 만약 랜덤 하게 선택된 가중치가 Local minimum 가까이에 있고, Local minimum에 수렴해버리면, 실제 목표인 Global  minimum을 찾지 못하는 문제가 발생할 수 있다.

• 만약, 학습률(Learning Rate)을 너무 크게 설정한다면, Global minimum에 가까운 곳에서 시작한다 할지라도, 구간을 뛰어넘어 Local minimum에서 수렴할 수도 있다.
• 그러나, 실제로는 모델의 학습이 지역 최소값(Local minimum)에 빠져, 최적의 가중치를 못 찾는 일이 발생할 위험은 그리 크지 않다.

• 학습 시 가중치를 초기화하여 반복하여 최적해를 찾아가므로, $\beta$에서 수렴하여 Loss값이 0 가까이 떨어지지 못한다할지라도, 시작 위치가 다른 가중치에서 전역 최소값(Global minimum)에 수렴하여 Loss값이 0에 수렴할 수 있다.
• 즉, 모든 초기화된 가중치가 지역 최솟값에 수렴할 수 있는 위치에 존재하지 않는다면, 지역 최솟값 문제는 발생하지 않는다. 그러므로, Local minimum 현상의 발생 위험은 그리 크지 않다고 할 수 있다.

3. Plateau 문제

• 1. Local minimum 문제의 예시에서는 손실함수의 모양이 전반적으로 곡선을 그렸으나, 손실 함수의 안에는 평탄한 영역이 존재하기도 한다.

• 위 그래프에서 Plateau(플래튜)라고 불리는 평탄한 영역에서는 학습 속도가 매우 느려지며, 느려지다 못해 정지해버릴 위험이 존재한다.
• 경사 하강법의 공식을 보면, "현 지점의 기울기 X 학습률"을 통해 다음 가중치를 결정하는데, 평탄한 영역의 기울기는 매우 낮기 때문에 이동거리가 갈수록 줄어들게 되고, 그로 인해 더 이상 학습이 일어나지 않는 가중치 소실(Gradient Vanishing) 현상이 발생할 수 있다.
• 이러한 Plateau 현상이 발생하면, 극솟값에 수렴하지 못해, 학습 시간이 매우 길어지고, 경사하강법의 랜덤 한 가중치에서 현재의 기울기를 힌트로 기울기가 0인 극솟값에 수렴시켜 최적해를 찾는다는 알고리즘이 제대로 작동하지 못하게 된다.

4. Zigzag 문제

• 지금까지 경사하강법을 설명할 때, 이해하기 용이하도록 가중치($w$)가 1개만 있는 2차원 그래프를 사용했으나, 실제론 가중치의 수가 매우 많다. 이번엔 가중치가 2개인($w_1, w_2$) 3차원 그래프를 등고선으로 그려보자.

• 위 그래프는 2개의 매개변수($w_1, w_2$)에 대한 손실 함수를 등고선으로 그린 것이다.
• 가중치의 스케일(크기)이 동일하다면, 최적해로 바로 찾아갈 수 있으나, 가중치는 모르는 임의의 값이므로, 스케일이 동일하리란 보장이 없다.
• 만약, 가중치 스케일이 다르다면, 다음과 같은 현상이 발생하게 된다.

• 두 매개변수 $w_1$의 스케일이 $w_2$보다 크다보니, 손실 함수는 $x$축 방향 가중치인 $w_1$의 변화에 매우 둔감하고, $y$축인 $w_2$의 변화에 매우 민감하다.
• 즉, $w_2$의 크기가 $w_2$에 비해 매우 작다보니, $w_2$가 조금만 변해도 손실 함수는 크게 변하게 되어, 두 매개변수의 변화에 따른 손실 함수 변화가 일정하지 않다.
• 위 경우는 매개변수가 2개밖에 존재하지 않았으나, 실제에서는 그 수가 수백만개에 달할 수 있을 정도로 많기 때문에 이러한 Zigzag 현상은 더욱 복잡해지며, 그로 인해 최적해를 찾아가기가 어려워지고, 학습 시간 역시 길어지게 된다.

 지금까지 경사하강법의 문제점에 대해 알아보았다. 머신러닝에서는 위 문제들을 해결하기 위해 경사 하강법을 효율적으로 사용하기 위한 최적화 기법(Optimizer)들이 매우 많다.

 예를 들어 다음 포스트에서 학습할 SGD나 가장 많이 사용되는 Adam, Momentum, Adagrad 등이 있는데, 각 최적화 알고리즘들은 데이터의 형태에 따라 그에 맞는 방법을 사용하길 바란다.

 다음 포스트에서는 최적화 기법의 가장 기초가 되는 확률적 경사 하강법(Stochastic Gradient Descent, SGD)에 대해 학습해보도록 하겠다.

[참조]

towardsdatascience.com/demystifying-optimizations-for-machine-learning-c6c6405d3eea

www.programmersought.com/article/59882346228/

nittaku.tistory.com/271?category=742607

 지금까지 가중치를 평가하는 방법인 손실함수(Loss Function)에 대해 학습해보았다. 그렇다면, 어떻게 손실함수를 기반으로 최적의 가중치를 찾아낼까?

 이번 포스트에서는 손실함수로부터 어떻게 경사 하강법이 나오게 되었는지를 이야기해보고, 경사하강법을 위주로 설명해보도록 하겠다.

손실함수와 경사하강법

1. 최적화(Optimizer)

• 최적화는 손실함수(Loss Function)의 결과값을 최소화하는 가중치를 찾아내는 것이 목적이다.
• 그렇다면, 손실함수의 개형은 어떻게 생겼을까?
• 예상한 값과 실제값의 차이인 제곱 오차(SE)를 가지고, 손실함수의 개형을 보도록 하자.

$$ SE = (y - \hat{y})^2 $$

• 이해하기 쉽도록 예측값을 변수(가중치)가 1개만 있는 퍼셉트론을 가져와보자
• 예측값은 선형이다(변수는 가중치인 $w$이며, $x$와 상관 없이, 가산성과 동차성이 성립한다.)

$$ \hat{y} = wx + b $$

• 제곱 오차의 $\hat{y}$에 예측값을 대입하고 식을 풀어보자.

$$ (y - \hat{y})^2 = (y - (wx + b))^2 = y^2 -2y(wx + b) + (wx + b)^2 = w^2x^2 + 2wxb + b^2 - 2wxy - 2yb + y^2 $$

• 위 식에서 변수는 $w$이므로, 위 함수는 1개의 최적해를 갖는 이차 함수 형태인 것을 알 수 있다.
• 그러므로, 손실함수의 개형은 다음과 같다.

2. 경사하강법(Gradient Descent)

• 경사 하강법은 1차 미분계수를 이용해 함수의 최소값을 찾아가는 방법으로, 함수 값이 낮아지는 방향으로 독립 변수 값을 변형시켜가면서 최종적으로 최소 함수 값을 갖도록 하는 독립 변수 값을 찾는 방법이다.
• 위에서 보듯, 손실함수의 개형은 1개의 최적해를 갖는 2차 함수의 형태이므로, 경사하강법을 사용하여, 최소 함수 값을 갖도록 하는 최적해(가중치)를 탐색해야한다.
• 경사 하강법은 임의의 가중치를 설정하여, 그 점에서의 기울기를 계산하고, 그 기울기를 힌트로 기울기가 0인 지점을 찾아간다.
• 손실 함수의 부호를 반전시켜, 최댓값을 찾는다면 경사 상승법(Gradient Ascent)이 되나, 동일한 것이므로, 굳이 사용하지 않는다.

• 위 그럼처럼 기울기는 손실함수에서 임의의 가중치에서 시작하며, 기울기가 음수인 경우에는 양의 방향으로 이동하고, 기울기가 양수인 경우에는 음의 방향으로 이동하여, 극솟값을 찾아간다.
• 여기서 움직이는 기울기(경사)는 가중치에 대하여 편미분 한 벡터이고, 이 가중치를 조금씩 움직인다.

3. 경사하강법 공식

• 경사 하강법을 공식으로 써보면 다음과 같다.

$$ x_{i+1} = x_i - \eta\bigtriangledown f(x_i) $$

• 여기서 $\eta$(eta, 에타)는 학습률(Learning Rate)이라 하며, 한 번의 학습에서 얼마나 이동할지를 정한다.
• $\bigtriangledown$는 벡터 미분 연산자로 델(del) 연산자라 하며 이 기호를 나블라(nabla) 기호라고 한다.
• 스칼라 함수 $f(x)$의 기울기는 $\bigtriangledown f$로 표현한다.
• 기울기는 $f$의 각 성분의 편미분으로 구성된 열 벡터로 정의하고, 아래와 같이 표시한다.

$$ \bigtriangledown f = (\frac{\partial f}{\partial x_1}, ..., \frac{\partial f}{\partial x_n}) $$

$$ \bigtriangledown f = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}) $$

• 예를 들어 함수 $f(x, y, z) = 2x + 3y^2 - sin(z)$의 기울기는 다음과 같다.

$$ \bigtriangledown f = (\frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} + \frac{\partial f}{\partial z}) =(2, 6y, -coas(z)) $$

• ko.wikipedia.org/wiki/%EA%B8%B0%EC%9A%B8%EA%B8%B0_(%EB%B2%A1%ED%84%B0)

• 즉, 경사하강법 공식은 현재의 위치 $x_i$에 학습률 $\eta$에 그 위치에서의 기울기 $\bigtriangledown f(x_i)$만큼을 곱한 값을 뺀만큼 위치를 이동시켜 다음 위치 $x_{i+1}$로 이동한다는 소리다.
• 여기서 학습률과 기울기 곱($\eta\bigtriangledown f(x_i)$)을 빼는 이유는 현재의 기울기의 반대방향으로 이동하여, 극소값에 도달하기 위해서이다.

4. 학습률(Learning Rate, LR)

4.1. 경사 하강법 공식에서의 학습률의 영향

• 위 경사 하강법의 공식에서 중요한 것은 학습률(Laerning Rate)인데, 이 학습률에 따라 경사 하강법 시, 이동하는 수준이 달라지게 된다.
• 예를 들어, 기울기가 2.5이고 학습률이 0.01이라면, 경사하강법 알고리즘은 이전 지점으로부터 0.025 떨어진 지점을 다음 지점으로 결정한다.
• 즉, "이동 거리 = 학습률 X 기울기"로 움직인다. 이는 기울기가 낮다면 학습률이 높다할지라도 움직이는 거리가 줄어든다는 소리이고, 큰 고랑에 빠진다면, 거기서 나오지 못하고 수렴할 수 있다는 소리다.

4.2. 학습률이 낮은 경우

• 학습률이 낮다면, 이동하는 거리가 짧으며, 경사하강법 공식에 의해 이동할수록 기울기가 더욱 감소하므로, 짧은 이동 거리가 더 짧아진다.
• 그로 인해, 경사 하강법 알고리즘이 수렴하기 위해 반복해야하는 데이터 양이 많아지므로, 학습 시간이 늘어나게 된다.

4.3. 학습률이 높은 경우

• 학습률이 지나치게 큰 경우, 크게 이동하므로, 수렴이 빨리 발생해 학습 시간이 적게 걸린다.
• 그러나, 너무 크게 이동하므로, 전역 최솟값(Global minimum)이 있는 영역을 건너 뛰어 지역 최솟값에서 수렴할 수도 있다.
  (이 부분은 다음 포스트에서 세세하게 다루도록 하겠다.)

 지금까지 손실함수를 최소화하는 방법으로 어째서 경사하강법을 사용하는지와 경사하강법이 어떠한 구조로 움직이는지에 대하여 학습해보았다.

 다음 포스트에서는 경사하강법의 한계점에 대해 학습해보도록 하겠다.