
지난 포스트에서는 기계학습에서 사용되는 최적화 알고리즘인 경사 하강법에 대하여 살펴보았다. 이번 포스트에서는 경사 하강법의 한계점에 대해 학습해보도록 하겠다.
경사 하강법의 한계점
- 앞서 손실함수를 기반으로 경사 하강법의 개형을 그려보았으나, 실제로는 저렇게 깔끔한 이차 함수 형태를 그리지 않는다.
- 퍼셉트론의 공식이 활성화 함수를 타게 되면, 손실 함수의 모습은 거시적인 관점에서 봤을 때는 최적해를 1개 가진 이차 함수의 형태를 그리긴 하지만, 그 모습이 울퉁불퉁해져 최적해에 수렴하기 어려워진다.
- 이번 포스트에서는 경사하강법의 한계점에 대해 하나하나 짚고 넘어가 보도록 하겠다.
1. 데이터가 많아질수록 계산량 증가
- 앞서, 경사하강법(Gradient Descent)은 신경망에서 출력되는 예측값(Predict)과 실제값(Label)의 차이인 손실 함수(Loss Function)의 값을 최소화하는 것이 목적이다.
- 그러나, 학습용 데이터 셋이 많아진다면, 당연히 계산량도 무지막지하게 많아지게 되는데, 그로 인해 학습 속도가 매우 느려지게 된다.
- 기계학습에는 아주 거대한 빅데이터가 사용되게 되는데, 이러한 퍼포먼스 문제는 결코 무시할 수 없는 문제다.
2. Local minimum(Optima) 문제
- 앞서 그린 대략적인 손실함수의 개형은 굉장히 매끈하였으나, 활성화 함수로 인해 그 모양이 울퉁불퉁해지게 되고, 그로 인해 최적해에 수렴하지 못할 수 있다.
- 아래 그래프를 보도록 하자.
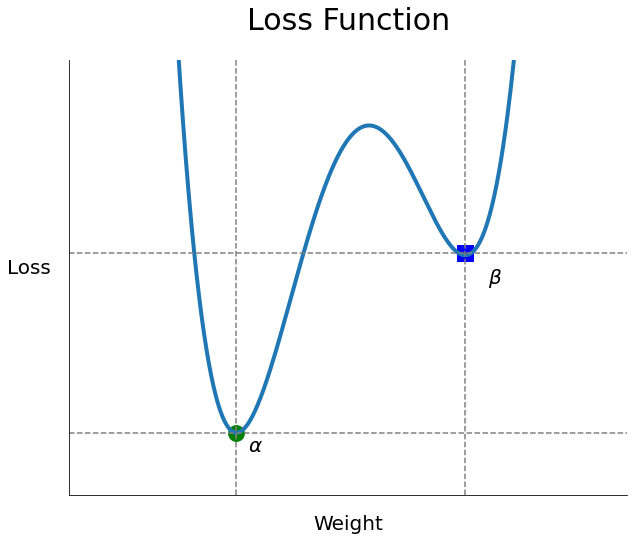
- 실제 손실함수의 모양은 위 그래프보다 울퉁불퉁한 정도가 심하나 이해를 돕기 위해 일부분만 가져와봤다.
- 위 그래프에서 $\alpha$를 전역 최소해(Global minimum), $\beta$를 지역 최소해(Local minimum)라 한다.

- 경사 하강법의 목적은 손실 함수에서 랜덤 하게 선택한 가중치를 미분하여 나온 결과를 힌트로 해서, 최적해를 찾아가는 것인데, 위 그래프처럼 만약 랜덤 하게 선택된 가중치가 Local minimum 가까이에 있고, Local minimum에 수렴해버리면, 실제 목표인 Global minimum을 찾지 못하는 문제가 발생할 수 있다.

- 만약, 학습률(Learning Rate)을 너무 크게 설정한다면, Global minimum에 가까운 곳에서 시작한다 할지라도, 구간을 뛰어넘어 Local minimum에서 수렴할 수도 있다.
- 그러나, 실제로는 모델의 학습이 지역 최소값(Local minimum)에 빠져, 최적의 가중치를 못 찾는 일이 발생할 위험은 그리 크지 않다.

- 학습 시 가중치를 초기화하여 반복하여 최적해를 찾아가므로, $\beta$에서 수렴하여 Loss값이 0 가까이 떨어지지 못한다할지라도, 시작 위치가 다른 가중치에서 전역 최소값(Global minimum)에 수렴하여 Loss값이 0에 수렴할 수 있다.
- 즉, 모든 초기화된 가중치가 지역 최솟값에 수렴할 수 있는 위치에 존재하지 않는다면, 지역 최솟값 문제는 발생하지 않는다. 그러므로, Local minimum 현상의 발생 위험은 그리 크지 않다고 할 수 있다.
3. Plateau 문제
- 1. Local minimum 문제의 예시에서는 손실함수의 모양이 전반적으로 곡선을 그렸으나, 손실 함수의 안에는 평탄한 영역이 존재하기도 한다.

- 위 그래프에서 Plateau(플래튜)라고 불리는 평탄한 영역에서는 학습 속도가 매우 느려지며, 느려지다 못해 정지해버릴 위험이 존재한다.
- 경사 하강법의 공식을 보면, "현 지점의 기울기 X 학습률"을 통해 다음 가중치를 결정하는데, 평탄한 영역의 기울기는 매우 낮기 때문에 이동거리가 갈수록 줄어들게 되고, 그로 인해 더 이상 학습이 일어나지 않는 가중치 소실(Gradient Vanishing) 현상이 발생할 수 있다.
- 이러한 Plateau 현상이 발생하면, 극솟값에 수렴하지 못해, 학습 시간이 매우 길어지고, 경사하강법의 랜덤 한 가중치에서 현재의 기울기를 힌트로 기울기가 0인 극솟값에 수렴시켜 최적해를 찾는다는 알고리즘이 제대로 작동하지 못하게 된다.
4. Zigzag 문제
- 지금까지 경사하강법을 설명할 때, 이해하기 용이하도록 가중치($w$)가 1개만 있는 2차원 그래프를 사용했으나, 실제론 가중치의 수가 매우 많다. 이번엔 가중치가 2개인($w_1, w_2$) 3차원 그래프를 등고선으로 그려보자.

- 위 그래프는 2개의 매개변수($w_1, w_2$)에 대한 손실 함수를 등고선으로 그린 것이다.
- 가중치의 스케일(크기)이 동일하다면, 최적해로 바로 찾아갈 수 있으나, 가중치는 모르는 임의의 값이므로, 스케일이 동일하리란 보장이 없다.
- 만약, 가중치 스케일이 다르다면, 다음과 같은 현상이 발생하게 된다.

- 두 매개변수 $w_1$의 스케일이 $w_2$보다 크다보니, 손실 함수는 $x$축 방향 가중치인 $w_1$의 변화에 매우 둔감하고, $y$축인 $w_2$의 변화에 매우 민감하다.
- 즉, $w_2$의 크기가 $w_2$에 비해 매우 작다보니, $w_2$가 조금만 변해도 손실 함수는 크게 변하게 되어, 두 매개변수의 변화에 따른 손실 함수 변화가 일정하지 않다.
- 위 경우는 매개변수가 2개밖에 존재하지 않았으나, 실제에서는 그 수가 수백만개에 달할 수 있을 정도로 많기 때문에 이러한 Zigzag 현상은 더욱 복잡해지며, 그로 인해 최적해를 찾아가기가 어려워지고, 학습 시간 역시 길어지게 된다.
지금까지 경사하강법의 문제점에 대해 알아보았다. 머신러닝에서는 위 문제들을 해결하기 위해 경사 하강법을 효율적으로 사용하기 위한 최적화 기법(Optimizer)들이 매우 많다.
예를 들어 다음 포스트에서 학습할 SGD나 가장 많이 사용되는 Adam, Momentum, Adagrad 등이 있는데, 각 최적화 알고리즘들은 데이터의 형태에 따라 그에 맞는 방법을 사용하길 바란다.
다음 포스트에서는 최적화 기법의 가장 기초가 되는 확률적 경사 하강법(Stochastic Gradient Descent, SGD)에 대해 학습해보도록 하겠다.
[참조]
towardsdatascience.com/demystifying-optimizations-for-machine-learning-c6c6405d3eea
Demystifying Optimizations for machine learning
Optimization is the most essential ingredient in the recipe of machine learning algorithms. It starts with defining some kind of loss…
towardsdatascience.com
www.programmersought.com/article/59882346228/
[2017CS231n] SEVEN: train the neural network (under) - Programmer Sought
First look at the sixth lecture: Data preprocessing. When we have the data normalized red, classifier weight matrix perturbation is not particularly sensitive, more robust. The left classifier little changes that will undermine the classification results.
www.programmersought.com
nittaku.tistory.com/271?category=742607
11. Optimization - local optima / plateau / zigzag현상의 등장
지난시간까지는 weight 초기화하는 방법에 대해 배웠다. activation func에 따라 다른 weight초기화 방법을 썼었다. 그렇게 하면 Layer를 더 쌓더라도 activation value(output)의 평균과 표준편차가 일정하게 유
nittaku.tistory.com
'Machine Learning > Deep Learning' 카테고리의 다른 글
| 딥러닝-6.3. 최적화(4)-확률적 경사 하강법(SGD) (0) | 2021.02.05 |
|---|---|
| 딥러닝-6.2. 최적화(3)-학습 단위(Epoch, Batch size, Iteration) (2) | 2021.02.05 |
| 딥러닝-6.0. 최적화(1)-손실함수와 경사하강법 (0) | 2021.02.03 |
| 딥러닝-5.5. 손실함수(6)-범주형 교차 엔트로피 오차(CCEE) (0) | 2021.02.01 |
| 딥러닝-5.4. 손실함수(5)-이진 교차 엔트로피 오차(BCEE) (0) | 2021.02.01 |