앞서 은닉층에서 자주 사용되는 함수인 렐루(ReLU)에 대해 알아보았다. 그러나, 렐루 함수는 음수인 값들을 모두 0으로 만들어 Dying ReLU를 만드는 문제점이 있다고 하였다.
렐루 함수는 아주 단순하지만, 그 단순함을 무기로 딥러닝의 길을 연 활성화 함수라 할 수 있고, 이러한 렐루 함수의 한계점을 보완하기 위해 다양한 활성화 함수들이 만들어졌으며, 지금도 만들어지고 있다.
이번 포스트에서는 렐루 함수의 단점을 보완하기 위해 만들어진 활성화 함수들에 대해 알아보겠다.
1. 리키 렐루(Leaky ReLU, LReLU)
- 렐루 함수의 한계점의 원인은 음수 값들이 모두 0이 된다는 것이었다.
- 이를 해결하기 위해, 음수를 일부 반영해주는 함수인 리키 렐루가 등장하게 되었다.
- 기존 렐루 함수는 음수를 모두 0으로 해주었다면,
- 리키 렐루는 음수를 0.01배 한다는 특징이 있다.
>>> import numpy as np
>>> import matplotlib.pyplot as plt
# Leaky ReLU를 만들어보자
>>> def Leaky_ReLU(x):
>>> return np.maximum(0.01*x, x)>>> x = np.arange(-100.0, 100.0, 0.1)
>>> y = Leaky_ReLU(x)
>>> fig = plt.figure(figsize=(8,6))
>>> fig.set_facecolor('white')
>>> plt.ylim(-5, 20)
>>> plt.title("Leaky ReLU", fontsize=30)
>>> plt.xlabel('x', fontsize = 15)
>>> plt.ylabel('y', fontsize = 15, rotation = 0)
>>> plt.axvline(0.0, color='gray', linestyle="--", alpha=0.8)
>>> plt.axhline(0.0, color='gray', linestyle="--", alpha=0.8)
>>> plt.plot(x, y)
>>> plt.show()
- 보시다시피 Leaky ReLU는 음수에 아주 미미한 값(0.01)을 곱하여, Dying ReLU를 막고자 하였다.
- 그러나, 음수에서 선형성이 생기게 되고, 그로 인해 복잡한 분류에서 사용할 수 없다는 한계가 생긴다.
- 도리어 일부 사례에서 Sigmoid 함수나 Tanh 함수보다도 성능이 떨어진다는 이야기가 나올 때도 있다.
- 만약, 음수가 아주 중요한 상황이라면 제한적으로 사용하는 것을 추천한다.
파라미터 렐루(Parameter ReLU, PReLU)
- 렐루 함수가 0.01이라는 고정된 값을 음수에 곱해준다면, 파라미터 렐루는 이 값을 $\alpha$로 하여, 하이퍼 파라미터로써 내가 원하는 값을 줄 수 있도록 만든 활성화 함수다.
# Leaky ReLU를 만들어보자
>>> def Leaky_ReLU(x):
>>> return np.maximum(0.01*x, x)
# PReLU를 만들어보자
>>> def PReLU(x, a):
>>> return np.maximum(a*x, x)>>> x = np.arange(-100.0, 100.0, 0.1)
>>> y1 = Leaky_ReLU(x)
>>> y2 = PReLU(x,0.05)
>>> fig = plt.figure(figsize=(8,6))
>>> fig.set_facecolor('white')
>>> plt.ylim(-5, 20)
>>> plt.title("Leaky ReLU & PReLU", fontsize=30)
>>> plt.xlabel('x', fontsize = 15)
>>> plt.ylabel('y', fontsize = 15, rotation = 0)
>>> plt.axvline(0.0, color='gray', linestyle="--", alpha=0.8)
>>> plt.axhline(0.0, color='gray', linestyle="--", alpha=0.8)
>>> plt.plot(x, y1, c = "blue", linestyle = "--", label = "Leaky ReLU")
>>> plt.plot(x, y2, c = "green", label = "PReLU")
>>> plt.legend(loc="upper right")
>>> plt.show()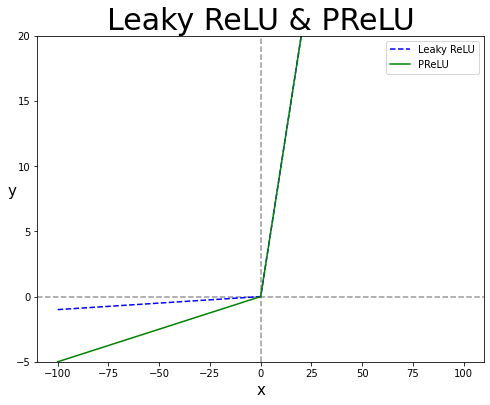
- PReLU는 Leaky ReLU와 그 성격이 상당히 비슷하지만, 음수의 계수인 $\alpha$를 가중치 매개변수처럼 학습되도록 역전파에 $\alpha$의 값이 변경되기 때문에, 대규모 이미지 데이터셋에서는 ReLU보다 성능이 좋다는 이야기가 있으나, 소규모 데이터셋에서는 과적합(Over fitting)될 위험이 있다.
- 또한, PReLU 역시 선형성을 띄기 때문에 복잡한 분류에서 사용하지 못할 수 있으므로, 주의해서 사용하는 것이 좋다.
- LReLU, PReLU 모두 기본으로는 ReLU 함수를 사용하고, 성능 개선 시, 활성화 함수를 해당 활성화 함수로 바꿔가며 실험해보고 사용하는 것을 추천한다.
2. ELU(Exponential Linear Unit)
- E렐루는 2015년에 나온 비교적 최근 방법으로, 각져 있는 ReLU를 exp를 사용해, 부드럽게(Smooth) 만든 것이다.
$$f(x) = \begin{cases}
x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (x > 0) \\
\alpha(e^x - 1) \ \ (x\leq 0)
\end{cases}$$
# ELU 함수를 만들어보자
>>> def ELU(x, a=1):
>>> return (x>0)*x + (x<=0)*(a*(np.exp(x) - 1))- 위 코드에서 (x>0)은 x가 0보다 큰 값만 True로 하여 1로 나머지 값은 0으로 만든다.
- (x <=0)은 0 이하인 값만 True로 하여 1로 하고 나머지 값은 0으로 만든다.
- 0보다 큰 경우 x가 곱해지고, 0 이하는 $exp(x) - 1$이 곱해진다.
- 각 반대되는 영역은 0이므로, 두 array을 합치면, 의도한 양수는 본래의 값, 나머지 값은 $exp(x) - 1$이 곱해져서 더해진다.
- 이러한 Masking을 이용한 Numpy 연산은 코드를 단순하게 하고, 연산 시간을 크게 줄이므로, 꼭 익히도록 하자.
>>> x = np.arange(-30.0, 30.0, 0.1)
>>> a = 1
>>> y = ELU(x,a)
>>> fig = plt.figure(figsize=(8,7))
>>> fig.set_facecolor('white')
>>> plt.ylim(-3, 25)
>>> plt.xlim(-20, 20)
>>> plt.title("ELU", fontsize=30)
>>> plt.xlabel('x', fontsize = 15)
>>> plt.ylabel('y', fontsize = 15, rotation = 0)
>>> plt.axvline(0.0, color='gray', linestyle="--", alpha=0.8)
>>> plt.axhline(0.0, color='gray', linestyle="--", alpha=0.8)
>>> plt.plot(x, y)
>>> plt.show()
- ELU는 ReLU와 유사하게 생겼으면서도, exp를 이용해 그래프를 부드럽게 만들고, 그로 인해 미분 시, 0에서 끊어지는 ReLU와 달리 ELU는 미분해도 부드럽게 이어진다.
- ERU는 ReLU의 대표적인 대안 방법 중 하나다.
- ERU는 ReLU와 달리 음의 출력을 생성할 수 있다.
- ERU는 LReLU나 PReLU와 달리 음에서도 비선형적이기 때문에 복잡한 분류에서도 사용할 수 있다.
- $\alpha$는 일반적으로 1로 설정하며, 이 경우 $x=0$에서 급격하게 변하지 않고, 모든 구간에서 매끄럽게 변하므로, 경사 하강법에서 수렴 속도가 빠르다고 한다.
- 그러나, ReLU에 비해 성능이 크게 증가한다는 이슈가 없으며, 되려 exp의 존재로 연산량이 늘어났기에 학습 속도가 ReLU에 비해 느려서 잘 사용하지 않는다.
SELU(Scaled Exponential Linear Unit)
- 일반적으로 ELU는 $\alpha$에 1을 넣으므로, PReLU처럼 $\alpha$를 하이퍼 파라미터 값으로 넣어 학습시킬 수 있게, ELU를 수정한 것이다.
- $\alpha$ 2개를 파라미터로 넣어 학습시키면, 활성화 함수의 분산이 일정하게 나와 성능이 좋아진다고 한다.
- 그러나 알파 값에 따라 활성화 함수의 결괏값이 일정하지 않아 층을 많이 쌓을 수 없다고 한다.
- SELU 역시 ReLU에 비해 성능이 그리 뛰어나지 않고, 연산만 늘어나므로, 정 쓰고자 한다면 SELU보다 ELU를 추천한다.
지금까지 ReLU와 유사한 ReLU의 형제들에 대해 알아보았다. LReLU, PReLU, ELU, SELU 중에 개인적으로는 ELU를 추천하지만, 소모되는 시간에 비해 성능 향상이 미비하거나 되려 성능이 내려가기도 하니 주의해서 쓰도록 하자.
cs231n 강의에서는 ReLU > LReLU or ELU 순으로 사용할 것을 이야기하였으며, 가능한 sigmoid는 사용하지 말라고 하였다.
이외에도 tanh함수를 대체하기 위해 고안된 softsign, ReLU를 부드럽게 꺾은 듯한 softplus와 Google이 최근 발표하였고, 높은 성능이 기대되는 Swish, ReLU와 LReLU를 일반화한 Maxout 등 다양한 활성화 함수가 존재하고, 지금도 새로 만들어지고 있다.
이러한 새로운 활성화 함수 중 성능이 괜찮다는 이슈가 있는 것은 추후 포스팅을 하도록 하고, 퍼셉트론에 기존의 계단 함수가 아닌 지금까지 학습해왔던 활성화 함수가 들어가 다층을 쌓아 만들어내는 신경망에 대해 차근차근 학습해보도록 하겠다.
혹여 활성화함수에 대해 더 관심이 있다면 아래 홈페이지를 참고하기 바란다.
www.tensorflow.org/api_docs/python/tf/keras/activations
Module: tf.keras.activations | TensorFlow Core v2.4.1
Built-in activation functions.
www.tensorflow.org
'Machine Learning > Deep Learning' 카테고리의 다른 글
| 딥러닝-4.1. 인공신경망(2)-신경망 연산(MLP) (0) | 2021.01.28 |
|---|---|
| 딥러닝-4.0. 인공신경망(1)-신경망 연산(SLP) (0) | 2021.01.28 |
| 딥러닝-3.4. 활성화함수(5)-렐루 함수(ReLU) (0) | 2021.01.27 |
| 딥러닝-3.3. 활성화함수(4)-하이퍼볼릭 탄젠트 함수(tanh) (0) | 2021.01.26 |
| 딥러닝-3.2. 활성화함수(3)-소프트맥스 함수(Softmax) (1) | 2021.01.26 |