728x90
반응형

이전 포스트에서 만든 모델의 결과는 그리 나쁘진 않았으나, 패턴이 아주 단순함에도 쉽게 결과를 찾아내지 못했고, 학습에 자원 낭비도 많이 되었다.
왜 그럴까?
특성 스케일 조정
- 특성 스케일 조정을 보다 쉽게 말해보면, 표준화라고 할 수 있다.
- 이번에 학습한 대상은 변수(다른 정보에 대한 벡터 성분)가 1개밖에 없어서 그나마 나았으나, 만약, 키와 몸무게가 변수로 주어져 벡터의 원소로 들어갔다고 생각해보자.
- 키나 몸무게는 그 자리 수가 너무 큰 값이다 보니, 파라미터 역시 그 값의 변화가 지나치게 커지게 되고, 그로 인해 제대로 된 결과를 찾지 못할 수 있다.
- 또한 키와 몸무게는 그 단위마저도 크게 다르다 보니, 키에서 160이 몸무게에서의 160과 같다고 볼 수 있다. 그러나 모두가 알다시피 키 160은 대한민국 남녀 성인 키 평균에 못 미치는 값이며, 몸무게 160은 심각한 수준의 비만이다. 전혀 다른 값임에도 이를 같게 볼 위험이 있다는 것이다.
- 이러한 표준화가 미치는 영향은 손실 함수에서 보다 이해하기 쉽게 볼 수 있는데, 이로 인해 발생하는 문제가 바로 경사 하강법의 zigzag 문제다.

- $w_1$과 $w_2$의 스케일 크기가 동일하다면(값의 범위가 동일), 손실 함수가 보다 쉽게 최적해에서 수렴할 수 있다.
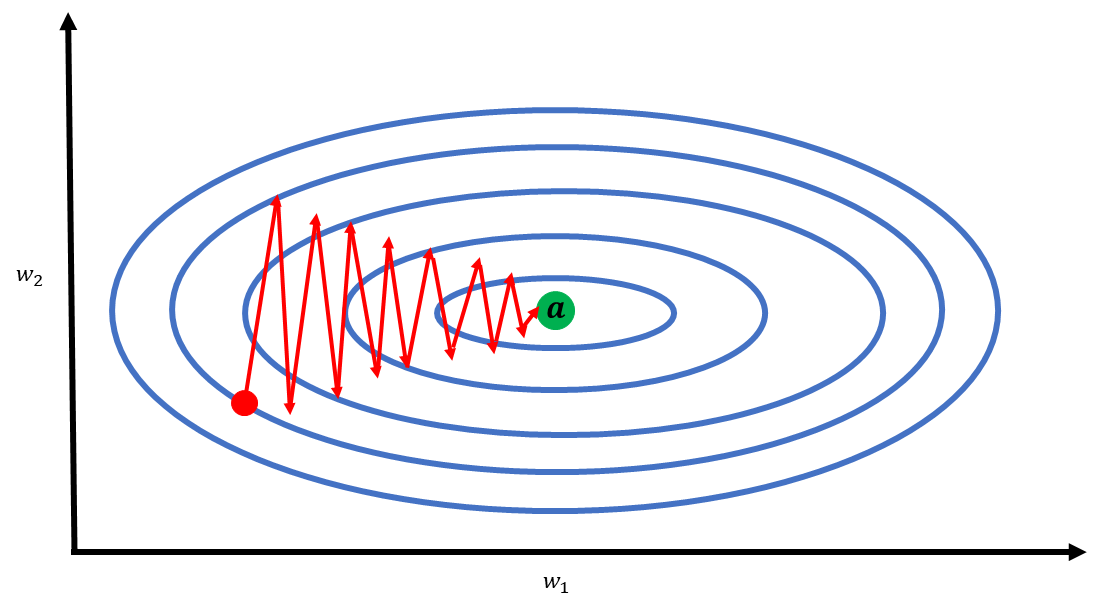
- $w_1$과 $w_2$의 스케일 크기가 많이 다르다면, 손실 함수는 쉽게 최적해에 수렴하지 못한다.
1. 특성 스케일 조정 방법
- 특성 스케일 조정 방법은 크게 2가지가 있다.
- 첫 번째는 특성 스케일 범위 조정이고, 두 번째는 표준 정규화를 하는 것이다.
A. 특성 스케일 범위 조정
- 특성 스케일 범위 조정은 말 그대로, 값의 범위를 조정하는 것이다.
- 바꿀 범위는 [0, 1]이다.
- 이 방법에는 최솟값과 최댓값이 사용되므로 "최소-최대 스케일 변환(min-max scaling)"이라고도 한다.
- 공식은 다음과 같다.
$$ x_{norm} = \frac{x_i-x_{min}}{x_{max}-x_{min}} $$
- 위 공식에서 $x_i$는 표준화를 할 대상 array다.
- 범위 축소에 흔히들 사용되는 해당 방법은, 가장 쉽게 표준화하는 방법이지만, 값이 지나치게 축소되어 존재하던 이상치가 사라져 버릴 수 있다.
- 특히나, 이상치가 존재한다면, 이상치보다 작은 값들을 지나치게 좁은 공간에 모아버리게 된다.
B. 표준 정규분포
- 표준 정규분포는 평균 = 0, 표준편차 = 1로 바꾸는 가장 대표적인 표준화 방법이다.
- 공식은 다음과 같다.
$$ x_{std} = \frac{x_i - \mu_x}{\sigma_x} $$
- 위 공식에서 $x_i$는 표준화 대상 array다.
- 표준 정규분포로 만들게 되면, 평균 = 0, 표준편차 = 1로 값이 축소되게 되지만, 여전히 이상치의 존재가 남아 있기 때문에 개인적으론 표준 정규분포로 만드는 것을 추천한다.
특성 스케일 조정에서 가장 중요한 것은, 조정의 기준이 되는 최솟값, 최댓값, 평균, 표준편차는 Train Dataset의 값이라는 것이다. 해당 방법 사용 시, Train Dataset을 기준으로 하지 않는다면, Test Dataset의 값이 Train Dataset과 같아져 버릴 수 있다.
2. 표준 정규분포를 이용해서 특성 스케일을 조정해보자.
# Import Module
import pandas as pd
import numpy as np
from tensorflow import keras
from tensorflow.keras.layers import Dense
# Dataset Setting
def f(x):
return x + 10
# Data set 생성
np.random.seed(1234) # 동일한 난수가 나오도록 Seed를 고정한다.
X_train = np.random.randint(0, 100, (100, 1))
X_test = np.random.randint(100, 200, (20, 1))
# Label 생성
y_train = f(X_train)
y_test = f(X_test)
# Model Setting
model = keras.Sequential()
model.add(Dense(16, activation='relu'))
model.add(Dense(1, activation='linear'))
# Compile: 학습 셋팅
opt = keras.optimizers.Adam(learning_rate=0.01)
model.compile(optimizer=opt, loss = 'mse')mean_key = np.mean(X_train)
std_key = np.std(X_train)
X_train_std = (X_train - mean_key)/std_key
y_train_std = (y_train - mean_key)/std_key
X_test_std = (X_test - mean_key)/std_key- 앞의 모델 생성 및 Compile 단계까진 동일하나, 뒤에 표준화 과정이 추가된다.
- Train Dataset의 평균과 표준편차는 test의 Dataset이 나중에 주어져 현재 할 수 없거나, predict의 결과 원상 복귀에 사용되므로, 따로 Scalar 값을 빼놓자.
>>> model.fit(X_train_std, y_train_std, epochs = 100)
Epoch 1/100
4/4 [==============================] - 0s 1ms/step - loss: 0.5749
Epoch 2/100
4/4 [==============================] - 0s 1ms/step - loss: 0.2483
Epoch 3/100
4/4 [==============================] - 0s 3ms/step - loss: 0.0814
Epoch 4/100
4/4 [==============================] - 0s 2ms/step - loss: 0.0217
Epoch 5/100
4/4 [==============================] - 0s 2ms/step - loss: 0.0378
Epoch 6/100
4/4 [==============================] - 0s 1ms/step - loss: 0.0402
...
Epoch 95/100
4/4 [==============================] - 0s 2ms/step - loss: 4.5394e-06
Epoch 96/100
4/4 [==============================] - 0s 1ms/step - loss: 5.2252e-06
Epoch 97/100
4/4 [==============================] - 0s 2ms/step - loss: 5.7370e-06
Epoch 98/100
4/4 [==============================] - 0s 2ms/step - loss: 5.9242e-06
Epoch 99/100
4/4 [==============================] - 0s 2ms/step - loss: 5.8228e-06
Epoch 100/100
4/4 [==============================] - 0s 2ms/step - loss: 5.6276e-06
<tensorflow.python.keras.callbacks.History at 0x234ff82a520>- 이전에 비해 적은 epochs(=100)로 빠르게 손실 값이 0에 수렴하는 것을 볼 수 있다.
- 결과를 보도록 하자.
pred = model.predict(X_test_std.reshape(X_test_std.shape[0]))
# 원상복구
pred_restore = pred * std_key + mean_key
predict_DF = pd.DataFrame({"predict":pred_restore.reshape(pred_restore.shape[0]), "label":y_test.reshape(y_test.shape[0])})
predict_DF["gap"] = predict_DF["predict"] - predict_DF["label"]
predict_DF
# RMSE로 Accuracy를 확인해보자.
>>> print("Accuracy:", np.sqrt(np.mean((pred_restore - y_test)**2)))
Accuracy: 0.07094477537881977- 이전에 비해 확실히 빠르게 최적화가 되었으나, 여전히 예측값은 원하는 수준에 미치지 못한다.
- 굉장히 단순한 패턴임에도 불구하고, 아직까지 약간 다르다.
이 정도로 단순한 패턴이라면, 예측값과 실제값의 차이가 거의 없어야 하나, 아직까지 차이가 크다는 생각이 든다. 다음 포스트에서는 최종적으로 한 가지를 수정하고, 해당 코드를 최종적으로 정리해보도록 하자.
728x90
반응형
'Machine Learning > TensorFlow' 카테고리의 다른 글
| Tensorflow-1.5. 기초(6)-기초 모델 만들기(1)-변수 2개인 경우 (0) | 2021.02.08 |
|---|---|
| Tensorflow-1.4. 기초(5)-하이퍼 파라미터 튜닝 (0) | 2021.02.08 |
| Tensorflow-1.2. 기초(3)-학습하기(2) (2) | 2021.02.08 |
| Tensorflow-1.1. 기초(2)-학습하기(1) (0) | 2021.02.08 |
| Tensorflow-1.0. 기초(1)-데이터 셋 만들기 (0) | 2021.02.07 |