만년필잉크의 데이터 분석 지식 저장소

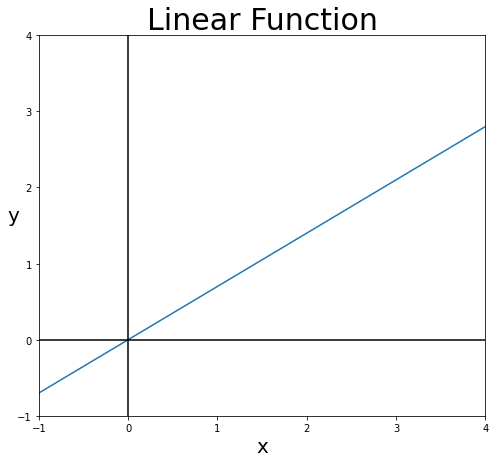
 지난 포스트에서 퍼셉트론의 가장 기본이 되는 활성화 함수인 계단 함수(Step Function)를 학습하였으며, 선형 함수(Linear Function)의 한계점에 대해서도 학습해보았다.

 선형 함수는 층을 쌓는 것이 무의미해진다는 단점이 있고, 비선형함수 중 하나인 계단 함수는 값의 크기에 대한 정보가 소실된다는 단점이 있다.

 이번 포스트에서는 이 두 단점이 해결된 비선형 함수 중 하나인 시그모이드 함수에 대해 학습해보겠다.

시그모이드 함수(Sigmoid Function)

계단 함수는 출력을 0과 1로 이진 값만 반환하며, 그 사이에 있는 값은 무시한다는 단점이 있었다. 그렇다면, 앞서 봤던 계단 함수의 각진 부분이 매끄러워진다면 어떨까?

1. 로지스틱 회귀 모델과 오즈(Odds)

• 통계학을 조금이라도 공부해봤거나, 분석에 관심 있는 사람이라면, 이진 분류의 대표적인 모델 중 하나인 로지스틱 회귀(Logistic regression)에 대해 들어봤거나, 알고 있을 것이다.
• 시그모이드 함수를 설명하기 앞서 로지스틱 회귀 모델의 오즈(Odds)를 이야기 해보겠다.

오즈(Odds)

• 오즈는 성공과 실패의 비율이다.
• 확률(Probability)과 뉘앙스가 꽤 다른 확률로
• "사건 A가 일어날 확률 / 사건 A가 일어나지 않을 확률"을 말한다.

$$ Odds = \frac{P}{1-P} $$

오즈비(Odds ratio)

• 참고로 오즈비(Odds ratio)와 오즈(Odds)를 헷갈리는 경우가 종종 있는데, 오즈비는 우리말로 교차비라고 하며, 서로 다른 집단의 오즈를 비교할 때 사용된다.
• 예를 들어 약품의 성능 대한 오즈비는, "약품 A를 먹어서 호전될 오즈 / 위약을 먹어서 호전될 오즈"이다.

$$ Test\ favorable\ Odds = \frac{Test\ favorable\ ratio}{Test\ unfavorable\ ratio} = \frac{\frac{60}{100}}{\frac{40}{100}} = 1.5$$

$$ Control\ favorable\ Odds = \frac{Control\ favorable\ ratio}{Control\ unfavorable\ ratio} = \frac{\frac{20}{100}}{\frac{80}{100}}=0.25$$

$$ OddsRatio = \frac{Test\ favorable\ Odds}{Control\ favorable\ Odds} = \frac{1.5}{0.25} = 6.0 $$

• 위 예시를 보면, 약품A의 효과는 위약의 효과의 6.0배임을 알 수 있다.

로짓 변환.

• 오즈에 자연로그를 취해서 로짓(Logit) 함수를 만들어보자.

$$ logit(P) = ln\frac{p}{1-p} = f(x) $$

$$ \frac{p}{1-p} = e^{f(x)},\ \  p=e^{f(x)}(1-p),\ \  p=e^{f(x)} - pe^{f(x)}, \ \  p(1+e^{f(x)})=e^{f(x)} $$

$$ p = \frac{e^{f(x)}}{1+e^{f(x)}} = \frac{1}{1+e^{-{f(x)}}} $$

• 위 함수를 로지스틱 시그모이드 함수(Logistic sigmoid function)이라고 하며, 줄여서 시그모이드 함수(Sigmoid function)이라고 한다.
• 여기서 $f(x)$에 회귀 분석과 같은 함수 식을 넣으면, 로지스틱 회귀 모델(Logistic Regression model)이 된다.

$$ f(x) = w^Tx = w_0x_0 + w_1x_1 + w_2x_2 +\ ... + w_mx_m  $$

2. 시그모이드 함수(Sigmoid Function)

• 시그모이드 함수를 파이썬에서 구현해보자.

# 시그모이드 함수
>>> def sigmoid(x):
>>>     return 1 / (1 + np.exp(-x))

>>> x = np.arange(-10.0, 10.0, 0.1)
>>> y = sigmoid(x)

# 캔버스 설정
>>> fig = plt.figure(figsize=(8,7)) # 캔버스 생성
>>> fig.set_facecolor('white')      # 캔버스 색상 설정

>>> plt.plot(x, y)
>>> plt.ylim(-0.1, 1.1)
>>> plt.xlim(-10, 10)
>>> plt.title("Sigmoid", fontsize=30)
>>> plt.xlabel('x', fontsize=20)
>>> plt.ylabel('y', rotation=0, fontsize=20)

>>> plt.yticks([0.0, 0.5, 1.0]) # 특정 축에서 특정 값만 나오게
>>> plt.axvline(0.0, color='k')
>>> ax = plt.gca()
>>> ax.yaxis.grid(True) # y축에 있는 모든 숫자에 회색 점근선을 그음

>>> plt.show()

• 시그모이드 함수는 0에서 1 사이의 함수이며, 값이 들어왔을 때, 0~1 사이의 값을 반환한다.
• 연속형 데이터이기 때문에 계단 함수가 끊기지 않는 매끄러운 모양으로 바뀐 것을 알 수 있다.
• 동시에 이상치가 들어온다 할지라도, 시그모이드 함수는 0과 1에 수렴하므로, 이상치 문제도 해결하면서, 연속된 값을 전달할 수 있다.

• 시그모이드 함수를 활성화 함수로 사용하면, 0과 1에 가까운 값을 통해 이진 분류를 할 수 있다.

3. 시그모이드 함수의 장점과 단점

A. 장점

• 출력 값의 범위가 0 ~ 1 사이이며, 매우 매끄러운 곡선을 가지므로, 후술 할 경사하강법을 시행할 때, 기울기가 급격하게 변해서 발산하는, 기울기 폭주(Gradient Exploding)가 발생하지 않는다.
• 분류는 0과 1로 나뉘며, 출력 값이 어느 값에 가까운지를 통해 어느 분류에 속하는지 쉽게 알 수 있다.

B. 단점

• 입력값이 아무리 크더라도, 출력되는 값의 범위가 매우 좁기 때문에 경사하강법 수행 시에 범위가 너무 좁아, 0에 수렴하는 기울기 소실(Gradient Vanishing)이 발생할 수 있다.

  B.1. 기울기 소실(Gradient Vanishing) 문제

• 시그모이드 함수는 아무리 큰 값이 들어온다 할지라도 0~1사이의 값만 반환하므로, 값이 일정 비율로 줄어들어 값의 왜곡이라 할 수는 없으나, 값이 현저하게 줄어들게 된다. 
• 또한, 출력 값의 중앙값이 0이 아닌 0.5이며, 모두 양수기 때문에 출력의 가중치 합이 입력의 가중치 합보다 커지게 된다.
• 이를 편향 이동(Bias Gradient)라 하고, 신호가 각 레이어를 통과할 때마다 분산이 계속 커지게 되어, 활성화 함수의 출력이 최댓값과 최솟값인 0과 1에 수렴하게 된다.
• 시그모이드 함수의 도함수는 $\sigma(1-\sigma)$인데, 도함수에 들어가는 함수의 값이 0이나 1에 가까울수록 당연히 출력되는 값이 0에 가까워지게 된다.
• 이로 인해 수렴되는 뉴련의 기울기(Gradient) 값이 0이 되고, 역전파 시 0이 곱해져서 기울기가 소멸(kill)되는 현상이 발생해버린다! 즉, 역전파가 진행될수록 아래 층(Layer)에 아무런 신호가 전달되지 않는 것이다!
• 이를 기울기 소실(Gradient Vanishing)이라 하며, 렐루 함수가 등장하기 전까지인 1986년부터 2006년까지 해결되지 않은 문제다.

  B.2. 학습 속도 저하 문제

• 시그모이드 함수의 출력값은 모두 양수기 때문에 경사하강법을 진행할 때, 그 기울기가 모두 양수거나 음수가 된다. 이는 기울기 업데이트가 지그재그로 변동하는 결과를 가지고 오고, 학습 효율성을 감소시켜 학습에 더 많은 시간이 들어가게 만든다.

 위 시그모이드 함수의 장단점을 간추려보면, 출력값이 너무 작아 제대로 학습이 안되는데다가 시간도 많이 잡아먹는다는 소리다.

 이는, 출력층에서 시그모이드 함수를 사용하는 것은 상관 없으나, 아래로 정보가 계속 흘러가는 은닉층(Hidden Layer)에서는 시그모이드 함수를 활성화 함수로 사용해서는 안된다는 소리다.

• 은닉층(Hidden Layer)은 입력층(시작), 출력층(끝) 사이에 있는 부분이다.
• 즉, 은닉층에는 앞서 말했던 선형 함수와 시그모이드 함수는 사용하지 않는 것이 좋다.
• 시그모이드 함수는 이진 분류를 하고자 하는 경우 출력층에서만 사용하는 것을 권고한다.
• 만약, 입력층에서 시그모이드 함수를 쓰고자 한다면, 이의 발전형인 하이퍼볼릭 탄젠트 함수를 사용하는 것을 추천한다.

 이번 포스트에서는 시그모이드 함수에 대해 간략하게 알아보았다. 시그모이드 함수는 이진 분류가 목적인 학습 모델에서 출력층에서 사용하는 것을 추천한다. 다음 포스트에서는 또 다른 활성화 함수인 소프트맥스 함수에 대해 학습해보겠다.

활성화 함수(Activation Function)

 이전 퍼셉트론에서 학습했던 내용을 보면, 입력층(Input layer)에서 전달된 정보(값)는 가중치를 받아 값이 변하고, 가중치를 받아 합산된 값($w_1x_1 + x_2x_2$)이 편향($b=-\theta$)보다 크거나 작다에 의해 정보가 전달(0 또는 1) 된다고 하였다.

 이번 포스트에서는 이 정보가 전달되는지, 즉 정보가 활성화 되는지 혹은 정보가 활성화된다면, 어떻게 활성화되어 출력 값을 생성해내는지를 결정하는 활성화 함수(Activation Function)에 대해 학습해보겠다.

1. 퍼셉트론에서 활성화 함수가 적용된 방법

• 우리가 퍼셉트론에서 사용했던 "임계값을 넘으면 정보가 전달되고, 임계값을 넘지 않으면 정보가 전달되지 않는다. "는 말을 활성화 함수에 초점을 맞춰서 보다 단순화된 공식으로 만들어보자.

$$ X = w_1x_1 + w_2x_2 + b $$

$$ h(x) = \begin{cases}
 0 \ \ (x \leq 0) \\ 
 1 \ \ (x >0) 
\end{cases} $$

• 위 공식에서 퍼셉트론 수식의 결과인 $X$는 활성화 함수 $h(x)$에 들어가게 되고, 그 결과는 출력 값 $y$로 나오게 된다. 이를 이해하기 쉽게 그림으로 그려보자.

• 이전에 봤던 퍼셉트론의 그림과 달리 파란색 노드가 새로 추가되지 않았는가?
• 이는 편향값이던 $b$를 노드와 동일한 형태로 만든 것이다. 이로써 $w_1, w_2, b$모두 단순하게 가중치라고 생각해도 충분한 상황이 만들어졌다.
• 앞에서도 설명하긴 했지만, 다시 한번 설명해보자면, 각 노드 1, $x_1, x_2$는 각각 $b, w_1, w_2$를 가중치로 받아 곱해지고, $X$로 합산되어 나온다. 합산된 $X$는 활성화 함수 $h(X)$가 되어 출력 값인 $y$가 최종적으로 도출되게 된다.

2. 계단 함수(Step Function)

• 이번엔 위 퍼셉트론에서 활성화 함수로 사용된, 계단 함수(Step Function)에 대해 초점을 맞춰보자.

$$ h(x) = \begin{cases}
 0 \ \ (x \leq 0) \\ 
 1 \ \ (x >0) 
\end{cases} $$

• 계단 함수라고 하니, 대체 무슨 소리인가 싶을 텐데, 위 공식을 그래프로 그려보면 쉽게 이해할 수 있다.

>>> import numpy as np
>>> import matplotlib.pyplot as plt

# 계단 함수1
>>> def step_function1(x):
>>>     if x <= 0:
>>>         return 0
>>>     else x>0:
>>>         return 1


# 계단 함수2
>>> def step_function2(x):
>>>     y = x > 0 
>>>     return y.astype(np.int)

• 위 코드를 보면, 위 코드는 단순히 "만약 x가 0 이하면 0을 반환하고, 0 초과이면 1을 반환하라"라는 의미로 단순하게 받아들여질 수 있는데, 아래 코드는 무슨 의미인지 잘 와 닿지 않을 수 있다.
• x.astype(np.int)는 데이터 x를 정수(int) 타입으로 바꿔준다는 것인데, x > 0의 결과는 x로 주어진 인자들이 0보다 큰지 작은지를 진리 값을 반환하며, True는 1, False는 0이므로, 위 step_function1과 같은 기능을 갖는 것이다.
• 코드를 쉽고 다른 사람도 이해하기 쉽게 짜려면 위 코드도 괜찮은 선택이다. 다만 상황에 따라 데이터의 양이 너무 많이 성능을 따져야한다면, 이런 식으로 같은 결과를 가지고 오지만, 다른 방법으로 돌아가는 코드도 짜서 성능 비교를 해볼 필요는 있다.

# 계단 함수를 그려보자
>>> np.arange(-5.0, 5.0, 0.1)
>>> y = step_function2(x)

# 캔버스 설정
>>> fig = plt.figure(figsize=(8,8)) # 캔버스 생성
>>> fig.set_facecolor('white')      # 캔버스 색상 설정

>>> plt.plot(x, y)
>>> plt.ylim(-0.5, 1.5)
>>> plt.xlim(-5, 5)
>>> plt.ylabel('y', fontsize = 20, rotation = 0)
>>> plt.xlabel('x', fontsize = 20)
>>> plt.title("Step Function", fontsize = 30)
>>> plt.show()

• 위 그래프를 보면, 마치 계단을 올라가듯이, x가 0을 기준으로 크게 변하는 것을 알 수 있다.
• 위 함수의 의미는 아주 순수하게 신경 세포의 전달 방법을 묘사한 기법으로, 출력되는 결과값이 갖는 정보가 너무 희석된다는 단점이 있다.
• 예를 들어, 합산된 값이 0.1인 경우와 1.0인 경우는 단순 산술적으로 10배 정도 차이가 있으나, 이를 모두 무시하고 단순하게 1로 전달하므로, 합산된 값의 강도에 대한 의미가 부여되지 않는다.

3. 선형 함수(Linear Function)

• 앞서 본 계단 함수는 합산된 값의 크기를 완전히 무시한다는 단점이 있다고 했다.
• 그렇다면, 정직하게 자신의 값을 나타내는 선형 함수(일차 함수)는 어떨까?

$$ y = kx (k: 상수)$$

# 선형 함수
>>> def Linear_Function(x, k):
    
>>>     return k*x


>>> x = np.arange(-5.0, 5.0, 0.1)
>>> y = Linear_Function(x, 0.7)

# 캔버스 설정
>>> fig = plt.figure(figsize=(8,7)) # 캔버스 생성
>>> fig.set_facecolor('white')      # 캔버스 색상 설정

>>> plt.plot(x, y)
>>> plt.ylim(-1, 4)
>>> plt.xlim(-1, 4)
>>> plt.axhline(c="black")
>>> plt.axvline(c="black")
>>> plt.ylabel('y', fontsize = 20, rotation = 0)
>>> plt.xlabel('x', fontsize = 20)
>>> plt.title("Linear Function", fontsize = 30)
>>> plt.show()

• 자 아주 단순한 일차 함수를 그려보았다.
• 그러나, 선형 함수는 활성화 함수로 사용할 수 없는 치명적인 단점을 2가지 가지고 있다.

선형 함수를 활성화 함수로 사용하지 못하는 이유

 1. 선형 함수는 층을 쌓는 의미가 없게 만든다.

• 예를 들어 3개 층으로 구성된 신경망이 있다고 가정해보자.

• 만약, 활성화 함수가 선형 함수 $h(x) = cx$라면, 각 노드에서 합쳐져 출력된 값들은 계수 c만큼 계속 곱해져 가며 커지기만 할 뿐이다.
• 즉, $h(x) = cx$를 쓰는 것과 $h(x) = ax \ \ (a = c^3)$를 쓰는 것과 큰 차이가 없는 형태가 된다.
• 물론, 이는 선형 함수를 절대 써선 안된다는 의미가 아니다. 선형 함수는 녹색 부분인 출력층에서 사용하는 것엔 문제가 없으나, 은닉층(파란색)에서 사용할 경우, 층이 쌓이는 것에 의미가 사라지기 때문에 사용하지 않는 것이 좋다.

2. 입력치에 이상치가 존재하는 경우, 분류를 불가능하게 만든다.

• 예를 들어, 학습 기간에 따른 합격 여부를 나눈다고 해보자.
• 공부 기간이 4일 이하인 경우, 불합격이 차지하는 비중이 많았고, 5일 이상에서 합격이 차지하는 비중이 훨씬 많았다. 그렇다면, 신경망은 4일을 기준으로 해서 합격 불합격 여부를 나누려고 학습을 할 것이다.
• 그러나, 만약, 누군가가 지나치게 공부를 오래하여, 1달 동안 공부를 해버렸다고 해보자. 이 경우 신경망은 어디를 기준으로 분류를 해야 할지 헷갈리게 된다.

 반대로 말하자면, 활성화 함수로 선형 함수를 사용하는 것은, 만약 다층 신경망이 아니거나, 입력치에 이상치가 없거나, 이상치를 조정하여 데이터에서 이상치가 존재하지 않는 형태로 만들었다면, 선형 함수를 쓰는 것에 큰 문제가 없다.

 지금까지 활성화 함수에서 가장 기초가 되는 계단 함수와 선형 함수에 대해 알아보았다. 선형 함수도 사용은 가능하나, 제한적으로 사용 가능하며, 다층 신경망에서 사용 시, 은닉층에서 사용해서는 안되므로, 주의해서 사용하길 바란다.

 다음 포스트에서는 분류를 할 때, 가장 많이 사용되는 두 활성화 함수인 Sigmoid, Softmax에 대해 알아보겠다.

 지난 포스트에서 퍼셉트론을 이용해 대표적인 논리 게이트인 AND 게이트, NAND 게이트, OR 게이트를 구현해보았다. 이번 포스트에선 또 다른 대표적인 논리 게이트인 XOR 게이트를 구현해보자.

1. XOR 게이트

• XOR 게이트는 배타적(자기 자신을 제외하고 나머지는 거부한다.) 논리합이라는 회로로, 변수 중 단 하나만 True(참 = 1) 일 때, True(=1)을 반환한다.
• XOR 게이트의 진리표는 다음과 같다.

• 자, 위 진리표를 구현할 수 있는 가중치($w_1, w_2, b$)를 찾을 수 있는가?

$$ y = \begin{cases}
 0, \ \ (w_1*0 + w_2*0 + b \leq 0) \\ 
 1, \ \ (w_1*0 + w_2*1 + b \leq 0) \\ 
 1, \ \ (w_1*1 + w_2*0 + b \leq 0) \\ 
 0, \ \ (w_1*1 + w_2*1 + b > 0) 
\end{cases} $$

• 위 공식에 들어 맞는 가중치를 찾는 것은 불가능하다.
• 그 이유는 앞서 말한 퍼셉트론 역시 회귀분석과 마찬가지로 선형성을 이용해서 0보다 크고, 작은 지를 구분해내기 때문이다.
• 위 말을 이해하기 쉽도록 위 진리표를 시각적으로 보자.

>>> import matplotlib.pyplot as plt

# 캔버스 설정
>>> fig = plt.figure(figsize=(8,8)) # 캔버스 생성
>>> fig.set_facecolor('white')      # 캔버스 색상 설정

>>> plt.title('XOR Gate, Visualization of True table', fontsize = 25)
>>> plt.ylim(-1, 4)
>>> plt.xlim(-1, 4)
>>> plt.axhline(color = 'k', alpha = 0.5)
>>> plt.axvline(color = 'k', alpha = 0.5)
>>> plt.xlabel("x1", fontsize = 20)
>>> plt.ylabel("x2", fontsize = 20, rotation = 0)

>>> plt.scatter([0, 1], [0, 1], s = 200, c = "green", marker="v")
>>> plt.scatter([0, 1], [1, 0], s = 200, c = "blue", marker="s")

>>> plt.show()

• 위에서 퍼셉트론의 구분 방법은 선형성을 이용한다고 했다.
• 선형성을 이용한다는 소리는 위 그래프에서 선 하나(퍼셉트론)로 파란 네모 점과 녹색 세모 점을 구분할 수 있어야 한다는 소리다.
• 직선이 아닌 곡선을 사용하지 않는한, 그 어떠한 방법으로도 하나의 직선으로는 위 점을 서로 다른 2개의 집단으로 구분해낼 수 없다.
• 즉, 퍼셉트론 하나로는 논리 게이트의 구현이 불가능하다는 것이고, 이는 퍼셉트론 하나로는 컴퓨터 같은 고등 연산을 수행할 수 없다는 것이다!

2. XOR 게이트의 해결 방법

 머리가 비상하게 좋은 친구라면(블로그 주인장은 그렇지 못하지만...), "앞서 만들었던 논리 게이트를 조합해서 이 문제를 해결할 수 있지 않을까?"라는 생각이 들지도 모른다.

 우리는 앞에서 AND, NAND, OR 게이트를 만들어보았고, 이들을 조합해서 문제를 해결할 수는 없을까?

• 위 그림을 보면, NAND, OR, AND 논리 게이트를 조합하면 우리가 위에서 만들었던 XOR 진리표의 결과를 출력하는 것을 알 수 있다.
• $x_1, x_2$는 일정하며, 어떤 논리 게이트를 결정하느냐에 따라 가중치($w_1, w_2, b$)만 바뀐다.
• 반대로 말하면, 가중치만 다른 퍼셉트론을 조합해서 내가 원하는 기능을 얻을 수 있다는 것이다.
• 자, 위 그림을 코드로 구현해보자. 이번에는 조금 더 코드 친화적으로 Numpy의 array를 이용해서 짜 보겠다.

>>> import numpy as np

>>> def step_function(x):
    
>>>     y = x > 0
    
>>>     return y.astype(np.int) 
        

>>> def Perceptron(x, dict_name, gate_name):

>>>     weight = dict_name[gate_name]
>>>     y = np.sum(x*weight['w']) + weight["b"]

>>>     return step_function(y)


>>> def XOR_gate(x):

>>>     array_x = np.array(x)
>>>     dict_W = {"AND":{"w":[0.5,0.5], "b":-0.7},
>>>               "NAND":{"w":[-0.5,-0.5], "b":0.7},
>>>               "OR":{"w":[0.5,0.5], "b":-0.2}}

>>>     y1 = Perceptron(array_x, dict_W, "NAND")
>>>     y2 = Perceptron(array_x, dict_W, "OR")
    
>>>     X = np.array([y1, y2])
>>>     Y = Perceptron(X, dict_W, "AND")
    
>>>     return step_function(Y)

>>> print("XOR Gate")
>>> print("----"*20)
>>> print("(0,0):", XOR_gate([0,0]))
>>> print("(0,1):", XOR_gate([0,1]))
>>> print("(1,0):", XOR_gate([1,0]))
>>> print("(1,1):", XOR_gate([1,1]))

XOR Gate
--------------------------------------------------------------------------------
(0,0): 0
(0,1): 1
(1,0): 1
(1,1): 0

• 위 코드에서 새롭게 ster_function()이라는 함수가 생겼는데, 이는 계단 함수로, 앞서 우리가 if문을 이용해서 합산된 결과가 0보다 클 때, 1을 반환하고, 0보다 작거나 같으면, 0을 반환하던 부분이다.
• 이를 활성화 함수(Activation Function)라 하는데, 활성화 함수를 통해 합산된 값을 출력할지, 출력한다면 어떻게 출력할지를 결정한다.
• 계단 함수는 이후 활성화 함수를 자세히 다룰 때, 다시 이야기하도록 하겠다.
• 위 코드를 보면, 오로지 가중치만 다른 퍼셉트론을 겹쳐서 사용했는데, XOR 게이트 문제를 해결한 것을 알 수 있다.
• 이렇게 2개 이상의 퍼셉트론을 쌓는 것을 다층 퍼셉트론이라고 한다.

3. 논리를 비약시켜보자.

• 위에서 우리는 2개 이상의 층(Layer)을 쌓아, 우리가 원하는 문제를 해결하였다.
• 이 곳에 사용된 층들은 오로지 가중치만 다르며, 이 가중치가 갖는 의미도 꽤 다르다.
• $w_1, w_2$ 같은 가중치는, 각 입력 신호에 부여되는 영향력(중요도)을 조절한다.
• $\theta$는 임계점이라 하였는데, 좌변으로 이항 시켜, $b$로 만들어주었고, 이는 편향(bias)라고 한다. 편향은 뉴런이 얼마나 쉽게 활성화되느냐에 영향을 미치며, $b$의 크기에 따라 활성화 함수가 작동하는지, 마는지가 결정된다.
• 지금까지 우리가 학습한 내용을 단순화시켜보면, 층을 많이 쌓고, 가중치를 맞게 설정해주면, 내가 원하는 결과를 얻을 수 있다는 것이다.
• 층을 많이 쌓는다는 것이 바로 우리가 아는 딥러닝(Deep Learning)의 딥(Deep)을 의미하며, 층이 많이 쌓인 신경망은 각 노드에서 다음 노드로 이동하는 신호에 부여하는 가중치를 다르게만 한다면, 구체적으로 함수 식을 모른다 할지라도 우리가 원하는 결과를 알 수 있다는 것이다.
• 그런데, 만약 그 가중치를 컴퓨터가 알아서 찾을 수 있다면 어떨까?
• 여기서 조금 어려워질지도 모르겠는데, 기계가 어떠한 방법(손실 함수)을 이용해서 가장 적합한 가중치를 찾아낸다면, 우리가 스스로 공부를 해서 어떤 결과를 도출하는 것처럼 컴퓨터도 적합한 가중치를 찾기 위한 활동, 즉! 학습과 동일하게 보이는 행동을 통해 데이터만 가지고 원하는 결과를 도출할 수 있다는 것이다.
• 여기서 "기계가 학습한다(Machine Learning)"이라는 말이 나오게 되는 것이며, 학습을 하되(가중치를 찾는 과정) 그것을 다층 레이어를 통해 찾아내는 것을 딥러닝(Deep Learning)이라 하게 되는 것이다.

 이번 포스트에선 퍼셉트론을 이용해 머신러닝이라는 단어와 딥러닝이라는 단어가 어떻게 만들어졌는지를 학습해보았다. 다음 포스트에서는 짧게 짚고 넘어갔던 활성화 함수에 대해 학습해보자.

 지난 포스트에서 기초적인 파이썬 코드를 사용하여, 퍼셉트론을 구현해보았다. 이번 포스트에서는 지난번에 생성한 퍼셉트론을 사용해서 논리 회로를 적용해보겠다.

논리회로(Logical circuit)

 1937년 클로드 섀넌(Claude Shannon)이 개발한 논리 회로(Logical Circuit)는 불 대수(Boolean algebra)를 물리적으로 구현한 것으로, 하나 이상의 논리적 입력값(True / False)이 들어가면, 그에 맞는 논리 연산(And / Or 등)을 수행하여 하나의 논리적 출력 값(True / False)을 얻는 전자 회로다.

 논리 회로는 다양한 불 대수의 조합을 통해 다양한 기능을 수행할 수 있는데, 이를 이용해서 컴퓨터 같은 고등 연산이 가능한 기계를 만들어 낼 수도 있다.

 여기서 AND, NOT, OR, XOR 등과 같은 기본이 되는 논리 연산을 수행하는 것을 논리 게이트(Logical gate)라 한다.

 만약, 앞에서 만들었던 퍼셉트론이 논리 게이트에 대해서도 적용 가능하다면, 퍼셉트론을 이용해서 컴퓨터도 만들 수 있지 않을까?

논리 게이트

1. AND 게이트

• AND 게이트는 우리가 코드를 짤 때, 익숙한 논리 연산자 AND와 같으며, 이는 집합에서 교집합에 해당한다. 교집합은 두 집합이 모두 참(True)일 경우, 참(True)을 반환하는 것이다.
• 두 집합에 대한 진리표를 만들어, 이를 보다 쉽게 이해해보자.

• 위 표를 볼 때, 1은 True(참)이라 생각하고, 0은 False(거짓)이라고 생각해보자.
• 위 표를 퍼셉트론의 공식에 맞게 고쳐보자.

$$ y = \begin{cases}
 0, \ \ \ w_1*0 + w_2*0 \leq \theta \\ 
 0, \ \ \ w_1*0 + w_2*1 \leq \theta \\ 
 0, \ \ \ w_1*1 + w_2*0 \leq \theta \\ 
 1, \ \ \ w_1*1 + w_2*1 > \theta  
\end{cases} $$

• 위 공식을 보면, 변수인 가중치($w_1, w_2$)와 임계값($\theta$)을 어떻게 설정하느냐로 AND 게이트를 구현할 수 있다는 것을 알 수 있다.
• 위 공식을 참으로 만드는 가중치와 임계값을 설정하여, AND 게이트를 구현해보자

# Perceptron
>>> def Perceptron(x1, x2, w1, w2, theta):
    
>>>     y = w1*x1 + w2*x2
    
>>>     if y <= theta:
>>>         return 0
>>>     elif y > theta:
>>>         return 1
    
    
# AND Gate를 구현해보자.
>>> w1, w2, theta = 0.5, 0.5, 0.8

>>> print("AND Gate")
>>> print("----"*20)
>>> print("(0, 0):", Perceptron(x1=0, x2=0, w1=w1, w2=w2, theta=theta))
>>> print("(0, 1):", Perceptron(x1=0, x2=1, w1=w1, w2=w2, theta=theta))
>>> print("(1, 0):", Perceptron(x1=1, x2=0, w1=w1, w2=w2, theta=theta))
>>> print("(1, 1):", Perceptron(x1=1, x2=1, w1=w1, w2=w2, theta=theta))

AND Gate
--------------------------------------------------------------------------------
(0, 0): 0
(0, 1): 0
(1, 0): 0
(1, 1): 1

• 위 코드를 보면, 가중치와 임계값을 0.5로 정했을 뿐인데, AND Gate와 동일한 결과가 나온 것을 알 수 있다.

2. NAND 게이트

• 이번에는 AND 게이트의 반대인 NOT AND 게이트인 NAND 게이트를 구현해보자.
• NAND 게이트는 AND 게이트의 반대이므로, 진리표는 다음과 같다.

# NAND Gate를 구현해보자.
>>> w1, w2, theta = -0.5, -0.5, -0.8

>>> print("NAND Gate")
>>> print("----"*20)
>>> print("(0, 0):", Perceptron(x1=0, x2=0, w1=w1, w2=w2, theta=theta))
>>> print("(0, 1):", Perceptron(x1=0, x2=1, w1=w1, w2=w2, theta=theta))
>>> print("(1, 0):", Perceptron(x1=1, x2=0, w1=w1, w2=w2, theta=theta))
>>> print("(1, 1):", Perceptron(x1=1, x2=1, w1=w1, w2=w2, theta=theta))

NAND Gate
--------------------------------------------------------------------------------
(0, 0): 1
(0, 1): 1
(1, 0): 1
(1, 1): 0

• NAND Gate는 AND Gate의 반대이므로, 가중치와 임계값을 모두 역수로 만들어주었다.

3. OR 게이트

• 다음은 또 다른 기본 논리 게이트 중 하나인 OR 게이트를 구현해보자.
• OR은 집합의 합집합에 해당하며, 둘 중 하나라도 True인 경우 True를 반환한다.

# OR Gate를 구현해보자.
>>> w1, w2, theta = 0.5, 0.5, 0.2

>>> print("OR Gate")
>>> print("----"*20)
>>> print("(0, 0):", Perceptron(x1=0, x2=0, w1=w1, w2=w2, theta=theta))
>>> print("(0, 1):", Perceptron(x1=0, x2=1, w1=w1, w2=w2, theta=theta))
>>> print("(1, 0):", Perceptron(x1=1, x2=0, w1=w1, w2=w2, theta=theta))
>>> print("(1, 1):", Perceptron(x1=1, x2=1, w1=w1, w2=w2, theta=theta))

OR Gate
--------------------------------------------------------------------------------
(0, 0): 0
(0, 1): 1
(1, 0): 1
(1, 1): 1

• OR 게이트도 오로지 가중치만 바꾸었는데, 우리가 원하는 값을 반환한 것을 볼 수 있다!

4. 퍼셉트론 공식 정리 및 코드 체계화

• 지금까지 퍼셉트론 코드를 짜보며, 이 코드를 보다 쉽게 바꿀 수 있다는 생각이 들지 않는가?
• 먼저 퍼셉트론에 사용된 공식에서 임계값 $\theta$를 왼쪽으로 이동시켜, 절편으로 만들면 어떨까?

$$ y = \begin{cases}
 0, \ \ \  (w_1x_1 + w_2x_2 + b \leq 0)  \\ 
 1, \ \ \  (w_1x_1 + w_2x_2 + b > 0) 
\end{cases} $$

• 좌변으로 이동하면서 $-\theta$로 부호가 음수로 바뀌었는데, 보기에 깔끔하지 않으니 부호가 양수인 $b$라는 절편으로 만들어보았다.
• 그런데 위 공식을 보면, 어디서 많이 본 공식과 굉장히 유사하지 않은가? 그렇다. 회귀식과 퍼셉트론의 공식은 동일하며, 이로써 퍼셉트론도 선형성을 따지는 것임을 알 수 있다.
• 위 내용을 코드에 반영하면서, 동시에 퍼셉트론으로 AND 게이트, NAND 게이트, OR 게이트를 구현할 때, 오로지 가중치만을 바꿨는데, 이를 보다 깔끔한 코드로 구현해보자.

>>> class Logical_gate:
    
>>>     def __init__(self, weight_dict):
        
>>>         self.weight = weight_dict


>>>     def Perceptron(self, x1, x2, key):

>>>         weight = self.weight[key]
>>>         w = weight["w"]
>>>         b = weight["b"]

>>>         y = w[0]*x1 + w[1]*x2 + b

>>>         if y <= 0:
>>>             return 0
>>>         elif y > 0:
>>>             return 1
        
>>>     def Run_Gate(self, key):

>>>         print(key + " Gate")
>>>         print("----"*20)
>>>         print("(0, 0):", self.Perceptron(0, 0, key))
>>>         print("(0, 1):", self.Perceptron(0, 1, key))
>>>         print("(1, 0):", self.Perceptron(1, 0, key))
>>>         print("(1, 1):", self.Perceptron(1, 1, key))
>>>         print("----"*20)
>>>         print("\n")

>>> weight_dict = {"AND":{"w":[0.5,0.5], "b":-0.5},
>>>                     "NAND":{"w":[-0.5,-0.5], "b":0.5},
>>>                     "OR":{"w":[0.5,0.5], "b":-0.2}}

>>> LG = Logical_gate()

>>> LG.Run_Gate("AND")
>>> LG.Run_Gate("NAND")
>>> LG.Run_Gate("OR")

AND Gate
--------------------------------------------------------------------------------
(0, 0): 0
(0, 1): 0
(1, 0): 0
(1, 1): 1
--------------------------------------------------------------------------------


NAND Gate
--------------------------------------------------------------------------------
(0, 0): 1
(0, 1): 0
(1, 0): 0
(1, 1): 0
--------------------------------------------------------------------------------


OR Gate
--------------------------------------------------------------------------------
(0, 0): 0
(0, 1): 1
(1, 0): 1
(1, 1): 1
--------------------------------------------------------------------------------

• 위 코드는 기존의 퍼셉트론 코드에 비해 더 어려워 보이긴 하지만, 일단 만들어 놓으면, 사용하기는 훨씬 쉽다.
• 새로운 논리 게이트를 구현하고자 하면, 딕셔너리인 weight_dict에 새로운 가중치($w_1, w_2, b$ 모두를 앞으로 단순하게 가중치로 부르겠다.)만 담으면 끝이다.

 지금까지 퍼셉트론을 이용해서 AND, NAND, OR 게이트를 가중치만 바꿔서 구현한 것을 살펴보았는데, 지금까지만 보면, 퍼셉트론이 논리 게이트에서도 잘 작동하는 것으로 보일 것이다.

 그러나, 앞서 말했듯 퍼셉트론도 선형성을 기반으로 결과를 도출하고, 그 결과가 활성화 함수인 계단 함수(이 부분은 뒤에서 자세히 다루겠다.)를 통해 출력되었는데, 이에 대한 반례가 존재한다.

 다음 포스트에서는 퍼셉트론의 논리 게이트 적용에서 반례인 XOR 게이트에 대해 학습해보고, 어째서 그런 문제가 발생하는지, 그리고 해결 방안은 무엇인지에 대해 학습해 보겠다.

 지난 포스트의 머신러닝, 딥러닝에 대한 설명이 잘 와 닿지 않았을 수 있다. 그러나 퍼셉트론(Perceptron)에 대해 학습해보면, 어떤 과정을 통해서 머신러닝이 이루어지고, 기계 학습이라는 단어의 학습이 정확히 무엇을 의미하는지 알 수 있을 것이다.

1. 신경 세포

 머신러닝 공부를 해보면 신경망(Neural Network)라는 단어를 종종 볼 수 있었을 것이다. 그리고 머신러닝에 사용되는 인공신경망이 사람의 신경을 흉내 내어 만들어졌다는 글도 나오는데, 대체 이게 무슨 소리일까?

• 위 그림은 인간의 신경 세포인 뉴런이다.
• 뉴런은 가지돌기(수상돌기)에 여러 신호가 도착하면 신경 세포체에서 이를 합치고, 합쳐진 신호가 특정 임계 값을 넘으면, 출력 신호가 생성되어 축삭 돌기를 통해 다음 뉴런으로 신호가 전달된다.
• 여기서 중요한 포인트는 다음과 같다.
  • A. 여러 신호가 신경 세포체로 전달된다.
  • B. 전달된 신호는 하나로 합쳐진다.
  • C. 합쳐진 신호가 특정 임계값을 넘으면, 전달된다.
• 나중에 다룰 이야기지만, 위 이야기에서 정보가 하나로 합쳐져서 전달되는 과정이 활성화함수(Activation function)를 나타내는 부분이라고 생각하자(이 건 나중에 다시 이야기하니깐 대충 넘기자)

2. 퍼셉트론(Perceptron)

• 퍼셉트론은 위에서 나온 신경 세포를 알고리즘화한 것으로, 딥러닝의 기본이 되는 개념이다.
• 퍼셉트론은 N개의 입력 받아 1개의 신호를 출력한다.
• 퍼셉트론은 받아들여 합친 신호가 임계값보다 크면 1을 출력하고, 임계값보다 작으면 0을 출력하여, 정보를 전달하거나 전달하지 않는다.

• 위 퍼셉트론 그림에서 원은 노드(Node) 혹은 뉴런(Neuron)이라고 부르며, 선은 엣지(Edge)라고 부른다.
• 노드에서 다음 노드로 정보가 전해질 때, 가중치($w_1$, $w_2$)가 곱해져 전달된다.
• 전달되는 값과 가중치가 곱해진 값($w_1x_1$)의 합($w_1x_1 + w_2x_2$)이 임계값 $\theta$(theta)보다 크면 1이, 작으면 0이 출력되는데, 이는 위에서 언급한 신경세포에서 신호가 전달되는 과정을 그대로 따라한 것과 같다.
• 이를 수식으로 나타내면 다음과 같다.

$$y = \begin{cases}
 0 \ \ \ (w_1x_1 + w_2x_2 \leq \theta) \\ 
 1 \ \ \ (w_1x_1 + w_2x_2 > \theta)
\end{cases}$$

• 위 함수를 보면, 위 신경세포에서 설명한 신호가 움직이는 과정을 쉽게 표현한 것임을 알 수 있다.

3. 퍼셉트론의 구현

• 앞서 입력 노드가 2개인 퍼셉트론의 함수를 적어보았다. 만약, 위 함수를 파이썬 코드로 구현한다면, 그것이 바로 퍼셉트론을 구현하는 것이 아니겠는가. 한 번 만들어보도록 하자.

# Perceptron 함수를 코드로 구현해보자
>>> def Perceptron(x1, x2, w1, w2, theta):

>>>     y = w1*x1 + w2*x2
            
>>>     if y <= theta:
>>>         return 0
                
>>>     elif y > theta:
>>>         return 1

• $x_1$과 $x_2$는 퍼셉트론의 노드이므로, 0과 1의 값만 나올 수 있다.
• $x_1=0,\ x_2=1,\ w_1=0.1,\ w_2=0.3,\ theta=0.6$으로 함수를 실행해보자 

>>> Perceptron(x1=0, x2=1, w1=0.1, w2=0.3, theta=0.6)
0

• 위 결과를 보면, 0*0.1 + 1*0.3 <= 0.6으로 나와 0이 반환된 것을 알 수 있다.
• 이를 보면, 가중치는 해당 노드에서 전달되는 정보의 중요도를 어느 정도나 강하게 줄 것인지를 따지는 것이고, 임계값은 받아들인 신호를 얼마나 타이트하게 평가할 것인가를 판단하는 수단이라는 것을 알 수 있다.

 지금까지 신경망의 기본이 되는 신경 세포, 퍼셉트론의 기본 개념에 대해 학습해보았다. 다음 학습에선 퍼셉트론을 이용하여 단순한 논리 회로를 적용하는 방법에 대해 학습해보도록 하겠다.

 해당 포스팅은 사이토 고키의 "밑바닥부터 시작하는 딥러닝"책을 참고하여 작성하였다. 해당 책은 꽤 얇고 내용도 이해하기 쉽게 써놨으므로, 머신러닝을 시작하는 초보가 읽기에 괜찮은 책이다. 시간 날 때, 한 번 읽어보기 바란다(참고로 PPL이 아니다! 내 돈 주고 내가 산 괜찮은 책 소개다!).

 현재 컴퓨터를 사용하는 모든 분야에서 가장 핫한 분야를 한 가지 고르라고 한다면, 장담컨대 "인공지능 > 머신러닝 > 딥러닝"을 꼽을 수 있을 것이다. 알파고 이후로 모든 매체에서는 인공지능, 머신러닝, 딥러닝이라는 단어를 외치고 있으며, 이 것이 중요하다는 것은 알겠는데 구체적으로 어떻게 중요한지, 그리고 이 것이 구체적으로 무엇인지를 제대로 설명해주는 곳은 많지가 않다.

 이번 포스트에서는 "인공지능 > 머신러닝 > 딥러닝"으로 이어지는 단어들에 대해 설명하고, 앞으로의 학습 방향에 대해 이야기해보도록 하겠다.

1. 인공지능(AI)이란?

 인공지능이라는 단어를 들으면 막연하게 "터미네이터 같은 인간과 유사한 생김새를 갖고 있으며, 인간보다 뛰어난 능력을 가진 존재"라는 생각이 들 것이다. 인공지능은 크게 General AI(일반적인 AI)와 Narrow AI(좁은 AI) 두 가지로 나뉘는데, 이를 설명해보면, 대충 감이 올 것이다.

General AI

• 영화에 나오는 인공지능으로 인간처럼 사고를 하며, 상황에 맞는 다양한 활동을 하는 인공지능을 말한다.
• 예를 들자면 자신의 다리로 계단이던 길이던 횡단보도던 알아서 돌아다니고, 필요에 따라 판단하여 택시나 버스를 타고, 에너지가 부족하다 싶으면 알아서 에너지도 충전하고, 회사에 출근해서 눈치를 살피는 그런 인간과도 같은 존재를 가리킨다.
• 이런 복합적인 기능을 자유자재로 동시에 수행하는 것은 아직까진 우리 상상 속에만 존재하며, 영화나 드라마에서만 나오는 존재다.

Narrow AI

• 말 그대로 좁은 영역에서의 인공지능을 말하며, 특정한 행동에 대해서만 특화 돼 있는 인공지능이다. 
• 가장 유명한 인공지능인 알파고는 바둑에 특화된 인공지능으로, 학습을 위해 바둑 기보들을 수집하고, 학습된 내용을 바탕으로 스스로 경쟁하여 바둑을 학습해, 바둑이라는 게임에서 승리할 수 있도록 만든 것이다.
• 학교, 뉴스, 4차 산업 혁명에 해당하는 인공지능이 바로 Narrow AI이다.
• 우리가 앞으로 학습할 인공지능이 이 곳에 해당한다.

2. 머신러닝(Machine Learning)이란?

 머신러닝은 위에서 이야기한 Narrow AI에 속하는데, 말 그대로 기계를 학습시킨다는 말이다.

 갓 태어난 아이는 성장을 하며 말을 배우고, 친구를 사귀는 법을 배우며, 국어, 영어, 수학 같은 학문을 배운다. 나아가 음악을 들었을 때, 이 음악이 어떤 음악이었는지 그 제목을 떠올리기도 하고, 그림을 보고 그림의 제목과 화가의 이름을 맞추기도 한다.

 우리가 처음으로 말을 배웠을 땐, 부모님이 하는 말을 계속 들어왔고, 부모님들은 사물에 사물 이름을 적은 메모장을 붙여놓는 방법 등을 통해 우리를 가르쳤다. 친구를 사귀는 법은 다양한 사람을 만나가며, 어떻게 하면 그들과 유대감을 쌓을 수 있는지 경험으로 익혔다. 국어, 영어, 수학 같은 학문은 계속 책을 보며, 문제를 푸는 방법과 사고하는 방법을 익혔다. 음악이나 그림을 판단하는 방법도 다양한 음악이나 그림을 접하면서 그것들을 구분하는 능력을 쌓았다.

 위 예시에서 우리는 오로지 데이터만을 가지고 지금의 복잡한 작업을 수월하게 할 수 있게 된 것이다. 컴퓨터를 이용한 기계학습 역시 이와 유사하게 이루어진다. 기본적인 머신러닝 알고리즘이 존재하고, 그 알고리즘에 데이터를 부어넣으면, 그 데이터가 가지고 있는 패턴을 찾아내, 그 패턴대로 분류하게 되는 것이 바로 머신러닝이다.

3. 딥러닝(Deep Learning)이란?

 1943년 논리학자 윌터 피츠(Walter Pitts)와 신경외과의 워렌 맥컬럭(Warren Mc Cullonch)은 "A Logical Calculus of Ideas Immanent in Nervous Activity"라는 논문에서 딥러닝의 기반이 되는 인공신경망이라는 개념을 등장시켰고, 인간의 신경세포를 모방한 퍼셉트론을 등장시켰다.

 퍼셉트론을 이용한 인공지능 연구능 처음엔 굉장한 인기를 끌었으나, 굵직 굵직한 사건이 터져 몇 번이고 사장될 위기에 처했었다. 처음엔 XOR 게이트로 인해 퍼셉트론은 선형 분류밖에 할 수 없다는 한계점이 등장했고, 이를 다층 퍼셉트론(MLP)라는 개념을 등장시켜 선형 분류의 한계점을 해결하였으나, MLP를 학습시킬 방법이 없다는 한계점이 또 등장하였다. 이는 오류역전파(Backpropagation of errors)라는 기법으로 해결하였으나, 층이 늘어날수록 기울기가 소실되는 문제가 또 등장하고, 은닉층 활성화 함수로 Sigmoid 대신 ReLU를 사용하여 해결하는 등 수많은 과정을 거쳐 지금의 딥러닝이 탄생하게 되었다.

 딥러닝이라는 이름이 생긴 이유도 기존의 다층 퍼셉트론(MLP)에 대한 부정적인 시선을 피하기 위해 딥러닝이라는 새로운 이름을 붙인 것이며, 다층 퍼셉트론(MLP)의 은닉층을 아주 많이 쌓기 때문에 딥(Deep)해진다. 즉, Layer가 깊어진다라는 의미에서 딥러닝이라는 이름이 붙은 것이다.

 딥러닝 역시 머신러닝의 한 갈래에 속하지만, 머신러닝에는 퍼셉트론을 포함하여 수많은 이론들이 존재하므로, 머신러닝과 딥러닝을 분리해서 생각하는 것이 좋다.

 해당 카테고리에서는 머신러닝에 대해서 학습할 계획이며, 딥러닝에 대해서는 Deep Learning 카테고리에서 따로 학습할 예정이다.