
인공신경망(Artificial Neural Network, ANN)
지금까지 퍼셉트론의 개념과 노드에 전달되어 합쳐진 신호들이 다음 노드로 전달될 때, 값이 어떤 방법으로 전달될지를 결정하는 활성화 함수에 대해 학습해보았다.
앞서 학습했던, 퍼셉트론은 계단 함수를 이용해서 신호를 전달할지(출력값 = 1), 전달하지 않을지(출력 값 = 0)를 정하였으며, XOR 게이트 실현에서 층을 여러 개 쌓자 단일층으로 해결하지 못했던 문제를 해결할 수 있었다.
여기서, 활성화 함수의 존재와 층을 여러 개 쌓는다. 이 부분에 초점을 맞추면, 인공신경망을 만들 수 있고, 이 인공신경망을 구현하고, 가장 적합한 가중치를 알아서 찾아내는 것이 바로 딥러닝(Deep Learning)이다.
본격적으로 신경망을 공부하기 전에 단층 퍼셉트론의 연산이 어떻게 이루어지는지 확인해보도록 하자. 단층 퍼셉트론의 연산 방법을 알게 되면, 다층 퍼셉트론의 구현은 이를 쌓아가기만 하면 된다.
1. m : 1 단층 퍼셉트론의 연산

- 위 그림에서 정보가 전달되는 방식을 수식으로 적어보면 다음과 같다.
$$ Z = w_1*x_1 + w_2*x_2 +b*1 $$
$$ y = h(Z) $$
- 여기서, $x_1=2, x_2=5, w_1 = 0.4, w_2 = 0.2, b = 0.7$이라고 가정해보자
- 위 수식에서 $Z$를 가장 빠르게 출력할 수 있는 방법은 백터 연산이다.
- 활성화 함수를 시그모이드 함수로 해서 구현해보자.
>>> import numpy as np
>>> def sigmoid(x):
>>> return 1 / (1 + np.exp(-x))
>>> x = np.array([2, 5, 1])
>>> w = np.array([0.4, 0.2, 0.7])
>>> Z = np.sum(x*w)
>>> sigmoid(Z)
0.9241418199787566- 도착점이 1개만 있는 경우, 입력층의 노드 수와 곱해지는 가중치 엣지의 수가 서로 동일하기 때문에, 길이가 동일한 벡터가 2개 나온다.
- 때문에, 벡터연산으로 쉽게 해결할 수 있다.
(numpy의 벡터 연산은 길이가 같은 벡터끼리 연산 시, 동일한 위치의 원소끼리 연산이 이루어지는 방식이다.) - m : 1 퍼셉트론은 이처럼 쉽게 연산이 가능했다. 그렇다면 입력층 노드의 수와 가중치 엣지의 수가 다른 m : n은 어떨까?
2. m : n 단층 퍼셉트론의 연산

- 참고로 위에서 각 엣지(Edge)별 가중치에 써놓은 숫자들이 무슨 뜻인지 이해가 안 갈 수 있으니, 이를 간략히 설명해보겠다.

- 가중치에서 위 괄호 안에 들어있는 값은 몇 번째 층(Layer)인지를 의미한다.
- 아래 숫자는 앞은 다음 층, 뒤는 앞 층을 이야기한다.
- 입력 노드의 값은 위에서부터 순서대로 1, 3, 5 라고 가정하자.
- 가중치 엣지의 값은 위에서부터 순서대로 0.3, 0.5, 0.4, 0.2, 0.7, 0.3이라고 가정하자.
- 편향 엣지의 값은 위에서부터 순서대로 0.2, 0.3이라 가정하자.
- 이를, 벡터 연산으로 구하고자 한다면, 각 벡터의 길이가 다르고, 이를 잘라서 $y_1$, $y_2$를 따로따로 연산하기엔 시간도 많이 걸리고 공식도 지저분해진다.
3. 행렬 곱
- 위와 같은 m : n 퍼셉트론은 행렬 곱을 사용한다면, 한방에 계산을 할 수 있다.
- 위 퍼셉트론을 수식으로 간소화하면 다음과 같다.
$$ Y = WX + B$$
$$ X = (x_1, x_2, x_3) = (1, 3, 5)$$
$$ B = (b_{1}^{(1)}, b_{2}^{(1)}) = (0.2, 0.3)$$
$$ W=
\begin{pmatrix}
w_{11}^{(1)} & w_{21}^{(1)}\\
w_{12}^{(1)} & w_{22}^{(1)}\\
w_{13}^{(1)} & w_{23}^{(1)}
\end{pmatrix}
=
\begin{pmatrix}
0.3 & 0.5\\
0.4 & 0.2\\
0.7 & 0.3
\end{pmatrix} $$
- 행렬 연산을 하기 위해선, 가장 먼저 배열이 어떻게 생겼는지를 확인해야 한다.
>>> X = np.array([1, 3, 5])
>>> B = np.array([0.2, 0.3])
>>> W = np.array([[0.3, 0.5],[0.4, 0.2],[0.7, 0.3]])
>>> print("X shape:", X.shape)
>>> print("B shape:", B.shape)
>>> print("W shape:", W.shape)
X shape: (3,)
B shape: (2,)
W shape: (3, 2)- 여기서 우리는 X와 W를 행렬곱할 것이다.
- 행렬곱을 간단하게 짚고 가자면 다음과 같다.
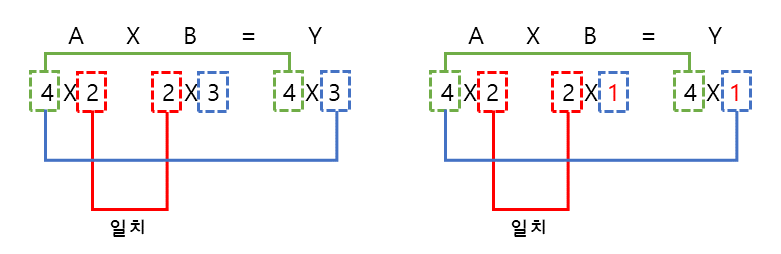
- 위 행렬 곱 방법을 보면, 서로 곱해지는 행렬에서 빨간 부분이 일치해야만 곱해지며, 출력되는 행렬의 녹색 부분이 행의 수, 파란색이 열의 수를 결정한다.
- 여기서 지금까지의 행렬에 대한 인식을 조금만 틀어보자.
- 행 = 데이터의 수
- 열 = 변수의 수
- 앞으로 이 인식을 하고 행렬 곱을 생각하게 된다면, 뒤에서 나올 n-차원 텐서의 연산에 대해서도 쉽게 이해할 수 있을 것이다(이에 대한 상세한 내용은 나중에 이야기하겠다.)
- 자, 위 수식을 함수로 구현해보자.
# 단층 퍼셉트론 연산
>>> Z = np.dot(X, W) + B
>>> Z
array([5.2, 2.9])- np.dot(A,B): 행렬 A와 행렬 B를 행렬 곱한다.
- 편향인 B는 행렬 X와 W의 곱과 길이가 동일한 벡터이므로(다음 노드의 수와 동일하다), 쉽게 벡터 합이 된다.
- 신경망에서 신호가 흘러가는 것은 행렬 연산을 통해 진행되며, 때문에 딥러닝에서 행렬 연산에 매우 유리한 GPU가 사용되는 것이다.
- 각 노드별 합산된 결과를 시그모이드 함수를 통해서 출력해보자.
# 시그모이드 함수를 활성화 함수로 사용
>>> sigmoid(Z)
array([0.9945137 , 0.94784644])
지금까지 단층 퍼셉트론(SLP)을 이용해서 신경망에서 연산이 어떻게 이루어지는지 확인해보았다. 다음 포스트에서는 다층 퍼셉트론(MLP)을 이용해서 신경망 연산을 학습해보도록 하자.
'Machine Learning > Deep Learning' 카테고리의 다른 글
| 딥러닝-4.2. 인공신경망(3)-신경망 학습 (0) | 2021.01.28 |
|---|---|
| 딥러닝-4.1. 인공신경망(2)-신경망 연산(MLP) (0) | 2021.01.28 |
| 딥러닝-3.5. 활성화함수(6)-ReLU Family (0) | 2021.01.27 |
| 딥러닝-3.4. 활성화함수(5)-렐루 함수(ReLU) (0) | 2021.01.27 |
| 딥러닝-3.3. 활성화함수(4)-하이퍼볼릭 탄젠트 함수(tanh) (0) | 2021.01.26 |
