
꽤 많은 블로그나 책에서 머신러닝을 다룰 때, 회귀모형, 로지스틱 회귀모형을 꼭 다루고 넘어가는데, 이번 포스트에서는 우리가 통계학에서 흔히 다루는 회귀모형과 딥러닝이 대체 어떤 관계길래 다들 회귀모형부터 다루는지에 대해 알아보고자 한다.
사실 우리는 이미 이전 포스트에서 회귀모형, 로지스틱 회귀모형을 만들어보았으며, 만약, 통계에 조금 익숙한 사람이라면, 분석된 결과나 그 과정을 보면서, 이게 회귀분석 아닌가? 하는 생각이 들었을지도 모른다(물론, Odd Ratio, $R^2$과 같은 익숙한 지표들이 그대로 등장하진 않았지만, 그것과 유사한 역할을 하는 지표를 이미 봤을 것이다).
회귀모형(Regression Model)
통계에 익숙한 사람이라면, 통계의 꽃인 회귀 모형에 대해 이미 잘 알고 있을 것이다. 우리가 기존에 학습했던, "Tensorflow-1.4. 기초(5)-하이퍼 파라미터 튜닝", "Tensorflow-2.4. 타이타닉 생종자 분류 모델(3)-하이퍼 파라미터 튜닝"에서 만들었던 모델이 바로 회귀모형이다.
1. 통계학과 딥러닝의 회귀모형
회귀모형에 대해 잘 모를 수 있으므로, 통계학에서의 회귀모형에 대해 아주 단순하게 설명해보도록 하겠다.
- 회귀모형은 데이터 간에 어떠한 경향성이 있다는 생각에서 시작된다.
- 회귀모형은 독립변수와 종속변수가 서로 인과 관계가 있다고 할 때, 독립변수가 변하면 종속변수가 변하게 된다.
회귀식: $ y = b_1x_1 + b_2x_2 + b_3x_3 + c $
- 회귀모형은 데이터에 가장 적합한 계수($b_1, b_2, b_3, c$)를 구하는 것이 목적이다.
- 회귀모형은 그 적합한 계수를 찾는 방법으로 평균 제곱 오차(MSE)를 사용한다.
(실제값과 예측값의 편차 제곱의 평균, 참고: "딥러닝-5.1. 손실함수(2)-평균제곱오차(MSE)")
회귀식은 퍼셉트론 공식과 아주 똑 닮았다("머신러닝-2.1. 퍼셉트론(2)-논리회로"). 그리고 딥러닝을 통해 우리는 각각의 파라미터(가중치와 편향)를 찾아낼 수 있다.
독립변수(Dataset이자 상수)의 변화에 따른 종속변수(Label, 상수)의 변화를 가장 잘 설명할 수 있는 계수(weight과 bias)를 찾아내는 것은 회귀분석이며, 이 점이 다층 퍼셉트론을 이용하여, 데이터 자체를 가장 잘 설명할 수 있는 파라미터를 찾아내는 딥러닝(Deep Learning)과 같다고 할 수 있다.
1.1. 이 밖의 회귀모형의 특징
- 회귀모형은 기본적으로 연속형 데이터를 기반으로 한다.
- 독립변수, 종속변수가 모두 연속형 데이터여야 한다.
- 연속형 데이터가 아닌 독립변수 존재 시, 이를 가변수(Dummy variable)로 만든다.
2. 데이터셋
이번 학습에서는 R을 사용해본 사람이라면 아주 친숙한 데이터 중 하나인 자동차 연비 데이터(MPG)를 이용해서 회귀모형을 만들어보도록 하겠다.
# Import Module
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np>>> dataset_path = keras.utils.get_file("auto-mpg.data", "http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")
Downloading data from http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data
32768/30286 [================================] - 0s 4us/step- tf.keras.utils.get_file()을 사용하면, 각종 데이터셋을 쉽게 가져올 수 있다.
- 데이터셋을 가지고 오는 곳은 UCI 머신러닝 저장소로 인터넷이 안 되는 환경이라면 데이터를 다운로드할 수 없으니, 조심하자.
- sklearn처럼 데이터셋을 Dictionary에 깔끔하게 저장하여, 데이터를 다운로드하면, 모든 데이터에 대한 정보가 있는 상태가 아니므로, 데이터에 대해 파악하기 위해선 UCI 머신러닝 저장소에서 데이터에 대해 검색하여, 데이터 정보를 찾아봐야 한다.
- 해당 포스팅에서는 "Tensorflow 공식 홈페이지의 자동차 연비 예측하기: 회귀"를 참고하여 데이터셋을 준비하였다.
column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight',
'Acceleration', 'Model Year', 'Origin']
Rawdata = pd.read_csv(dataset_path, names=column_names, na_values = "?",
comment='\t', sep=" ", skipinitialspace=True)
Rawdata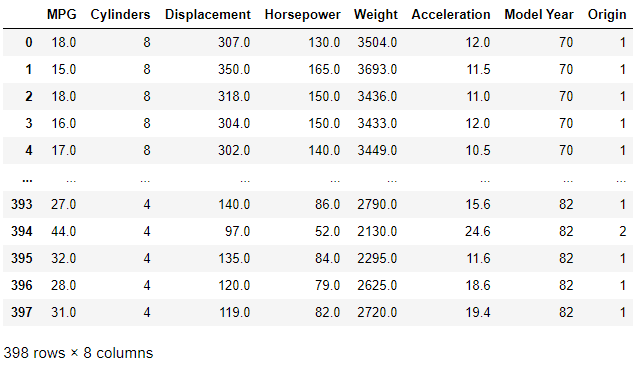
3. 데이터 전처리
3.1. 결측 값 처리
>>> Rawdata.isna().sum()
MPG 0
Cylinders 0
Displacement 0
Horsepower 6
Weight 0
Acceleration 0
Model Year 0
Origin 0
dtype: int64
>>> print("전체 데이터에서 결측값 행의 비율:", Rawdata.isna().sum(1).sum()/len(Rawdata))
전체 데이터에서 결측값 행의 비율: 0.01507537688442211- 위 결과를 보니, Horsepower에서 결측 값이 6개 발생한 것을 알 수 있다.
- 전체 데이터에서 결측 값 행의 비율을 보니 0.015로 매우 미미한 양이므로, 제거하도록 하자.
Rawdata.dropna(inplace = True)
3.2. 범주형 데이터의 원-핫 벡터화
- 칼럼 Origin은 숫자로 표시되어 있지만, 실제론 문자인 범주형 데이터이므로, 원-핫 벡터화 해주자.
(이는 회귀 모델에서의 가변수 처리와 매우 유사한 부분이라고 할 수 있다.)
# One-Hot Vector 만들기
def make_One_Hot(data_DF, column):
target_column = data_DF.pop(column)
for i in sorted(target_column.unique()):
new_column = column + "_" + str(i)
data_DF[new_column] = (target_column == i) * 1.0- 이전 참고 포스트에서 만들었던, 원-핫 벡터 코드보다 판다스의 성격을 잘 활용하여 만든 코드다
- DataFrame.pop(column): DataFrame에서 선택된 column을 말 그대로 뽑아낸다. 그로 인해 기존 DataFrame에서 해당 column은 사라지게 된다.
- (target_column == i) * 1.0: Boolearn의 성질을 사용한 것으로 target_column의 원소를 갖는 위치는 True로, 원소가 없는 곳은 False가 된다. 이에 1.0을 곱하여 int로 바꿔줬다. Python은 동적 언어이므로, 1.0을 곱해주어도 int형으로 변하게 된다.
3.3. 데이터셋 분리
- train set과 test set은 7:3으로 분리하도록 하겠다.
- validation set은 이 단계에서 뽑지 않고, 학습 과정(fit)에서 뽑도록 하겠다.
- MPG 변수는 연비를 의미하며 종속변수에 해당하므로, 이를 Label로 사용하겠다.
# Dataset 쪼개기
label = Rawdata.pop("MPG").to_numpy()
dataset = Rawdata.values
X_train, X_test, y_train, y_test = train_test_split(dataset, label, test_size = 0.3)
3.4. 특성 스케일 조정
- 해당 데이터 셋의 각 칼럼의 데이터는 다른 변수에서 나온 것이므로, 각각 변수별 기준으로 정규화해주어야 한다.
- 표준 정규 분포를 사용하여 특성 스케일 조정을 하도록 하겠다.
- 원-핫 벡터가 사용된 7:9까지의 열을 제외한 나머지 열에 대해 각각 특성 스케일 조정을 하겠다.
# 특성 스케일 조절
mean_point = X_train[:, :6].mean(axis=0)
std_point = X_train[:, :6].std(axis=0)
X_train[:, :6] = ((X_train[:, :6] - mean_point)/std_point)
X_test[:, :6] = ((X_test[:, :6] - mean_point)/std_point)- Numpy의 특징 중 하나인 Broadcasting 덕에 쉽게 정규화할 수 있다.
4. 모델 학습 및 평가
- 모델은 은닉층이 1개 있는 단층 퍼셉트론(Sigle-later Perceptron)으로 만들어보겠다.
(은닉층을 2개 이상 넣어 다층 퍼셉트론으로 만들어도 상관없다) - model은 Sequential 함수 안에 layer를 넣어주는 방법으로 만들어보겠다.
(추천하지는 않는 방법이지만 이런 방법도 있다는 것을 보여주고자 사용해보았다) - 출력층의 활성화 함수는 선형(Linear)으로 설정하였다.
(activation의 Default는 linear이므로, 따로 설정하지 않아도 된다) - 조기 종료(Early stop)를 콜백 함수로 주도록 하겠다.
# model 생성
model = keras.Sequential([
keras.layers.Dense(60, activation = "relu"),
keras.layers.Dense(1, activation = "linear")
])
# model compile 설정
opt = keras.optimizers.Adam(learning_rate=0.005)
model.compile(optimizer=opt, loss="mse", metrics = ["accuracy"])
# model 학습
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10, restore_best_weights=True)
model.fit(X_train, y_train, epochs=300, validation_split=0.2, callbacks=[early_stop])Epoch 1/300
7/7 [==============================] - 2s 248ms/step - loss: 572.1581 - accuracy: 0.0000e+00 - val_loss: 497.8600 - val_accuracy: 0.0000e+00
Epoch 2/300
7/7 [==============================] - 0s 19ms/step - loss: 516.3237 - accuracy: 0.0000e+00 - val_loss: 443.4315 - val_accuracy: 0.0000e+00
Epoch 3/300
7/7 [==============================] - 0s 18ms/step - loss: 454.6065 - accuracy: 0.0000e+00 - val_loss: 385.6940 - val_accuracy: 0.0000e+00
Epoch 4/300
7/7 [==============================] - 0s 19ms/step - loss: 390.3198 - accuracy: 0.0000e+00 - val_loss: 321.7114 - val_accuracy: 0.0000e+00
...
Epoch 79/300
7/7 [==============================] - 0s 8ms/step - loss: 5.6932 - accuracy: 0.0000e+00 - val_loss: 7.2688 - val_accuracy: 0.0000e+00
Epoch 80/300
7/7 [==============================] - 0s 8ms/step - loss: 5.9354 - accuracy: 0.0000e+00 - val_loss: 7.3990 - val_accuracy: 0.0000e+00
Epoch 81/300
7/7 [==============================] - 0s 8ms/step - loss: 5.5025 - accuracy: 0.0000e+00 - val_loss: 7.3694 - val_accuracy: 0.0000e+00
Epoch 82/300
7/7 [==============================] - 0s 8ms/step - loss: 5.8313 - accuracy: 0.0000e+00 - val_loss: 7.2677 - val_accuracy: 0.0000e+00
<tensorflow.python.keras.callbacks.History at 0x1e00b62b1f0># model 평가
>>> model.evaluate(X_test, y_test)
4/4 [==============================] - 0s 2ms/step - loss: 10.2492 - accuracy: 0.0000e+00
[10.24919319152832, 0.0]
5. 정리
- 출력층에 활성화 함수로 기본값인 선형 함수(Linear)가 사용되었다.
- 활성화 함수로 선형 함수가 사용되는 경우, 단순하게 이전 층에서 출력된 값에 대하여 선형 함수의 계수 값만큼만 곱하므로, 은닉층에서의 값을 보존한 상태로 출력하게 된다.
- 참고: "딥러닝-3.0. 활성화함수(1)-계단함수와 선형함수"
- 손실 함수로 평균 제곱 오차(MSE)를 사용하였다.
- 참고: "딥러닝-5.1. 손실함수(2)-평균제곱오차(MSE)"
- 회귀모형은 주어진 데이터가 어떠한 경향성을 갖고 있다는 가정하에 변수들 사이의 경향성을 가장 잘 설명할 수 있는 계수들을 찾아내는 것이다.
- 우리는 딥러닝 모델을 사용해서 Feature로 독립변수들을 넣었고, Label에 종속변수를 넣었다.
- 우리는 딥러닝 모델을 이용해 Feature가 Label에 대한 어떠한 경향성, 즉 패턴을 갖고 있다고 보고, 그 패턴을 나타내는 파라미터(weight, bias)를 찾아냈다.
- 회귀분석은 일반적으로 최소제곱법(OLS)을 통해 최적의 가중치를 찾아내지만, 우리는 최적의 가중치를 경사 하강법과 역전파를 통한 학습으로 찾아내었다.
- 출력층의 활성화 함수를 Sigmoid 함수로 사용하여 이진 분류 하면, 로지스틱 회귀모형(Logistic Regression model)이 된다.
지금까지 딥러닝(Deep Learning)을 사용하여, 회귀모델을 만들어보았다. 앞서 "딥러닝을 통해 이런 것도 되는구나!"하고 넘어갔던 부분들이 사실은 회귀모델이고, 회귀모델의 아이디어와 딥러닝의 아이디어의 유사한 부분에서 꽤 재미를 느꼈을 것이다.
다음 포스트에서는 Keras의 장점인 함수형 API를 이용해 모델을 만들어, 얕은 신경망(Wide model)과 깊은 신경망(Deep model)을 합친 Wide & Deep Learning에 대해 학습해보도록 하겠다.
'Machine Learning > TensorFlow' 카테고리의 다른 글
| Tensorflow-4.2. Wide & Deep Learning(2) - 다중입력모델 (0) | 2021.02.24 |
|---|---|
| Tensorflow-4.1. Wide & Deep Learning(1) - 함수형 API 사용하기 (0) | 2021.02.23 |
| Tensorflow-3.8. 이미지 분류 모델(8)-모델 저장과 불러오기 (0) | 2021.02.17 |
| Tensorflow-3.7. 이미지 분류 모델(7)-조기 종료와 콜벡 (0) | 2021.02.17 |
| Tensorflow-3.6. 이미지 분류 모델(6)-학습과정 확인 (0) | 2021.02.17 |