728x90
반응형

도수분포표와 시각화
앞서 도수분포표에서 봤듯, 도수분포표는 수집한 데이터의 분포를 알기 위해 사용한다. 그러나 여전히 숫자만으로 데이터를 파악하기 때문에 데이터의 분포를 명확하게 이해하기 어려울 수도 있다. 도수분포표를 시각화한다면, 보다 쉽게 데이터의 분포를 파악할 수 있다.
- 도수분포표의 시각화이므로, 들어간 데이터의 도수(빈도)를 시각화 하는 것이다.
- 파이썬으로 도수분포표를 시각화하는 방법은 크게 두가지가 있다.
- 범주화된 데이터를 사용해서 히스토그램을 만들기
- 도수분포표 생성 후, 도수분포표를 기반으로 그래프 그리기
- 개인적으로 추천하는 방법은 도수분포표를 먼저 생성하고, 그래프를 그리는 것으로, 도수분포표 연산이 한 번 이루어지고 나면, 나머지 과정은 자원을 거의 먹지 않는다.
- 도수분포표만 만들면, 이를 이용해서 히스토그램(막대그래프 사용), 도수분포다각형, 누적도수분포곡선 3가지를 모두 쉽게 그릴 수 있다.
1. 히스토그램
- 히스토그램은 가장 대표적인 도수분포표의 시각화 방법이다.
- 위에서 설명한 파이썬으로 도수분포표 시각화를 하는 첫 번째 방법으로, 원본 데이터(범주화가 된)를 사용해서 히스토그램을 그리는 것이다.
- 히스토그램은 막대그래프로 한 변수를 구성하는 각 집단의 빈도를 이용하여, 막대 그래프를 그리는 것이다.
- 이전 데이터에서 사용했던, 청소년건강행태조사 2019년 데이터에서 일부 변수만 추려낸 데이터를 사용해보자.
- "건강인지"를 히스토그램으로 나타내보자.
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltRawdata = pd.read_csv("Data_for_study.csv")# 한글 사용
plt.rc('font', family='NanumGothic')
# 전체 그래프 크기
fig = plt.figure(figsize=(8, 6))
# 히스토그래프 그리기
plt.hist(Rawdata.건강인지.to_numpy(), bins=9)
# x축 ticks 지정
plt.xticks(np.arange(1, 6), labels=["매우 좋음", "좋음", "보통", "나쁨", "매우 나쁨"])
plt.tick_params(axis="x", direction="in", labelsize = 12, pad = 20)
# title, xlabel, ylabel 지정
plt.title("건강인지 히스토그램", fontsize = 30, pad = 30)
plt.xlabel('건강인지', fontsize = 20, loc = 'center', labelpad = 20)
plt.ylabel('도수', fontsize = 20, rotation = 0, loc='center', labelpad = 30)
plt.show()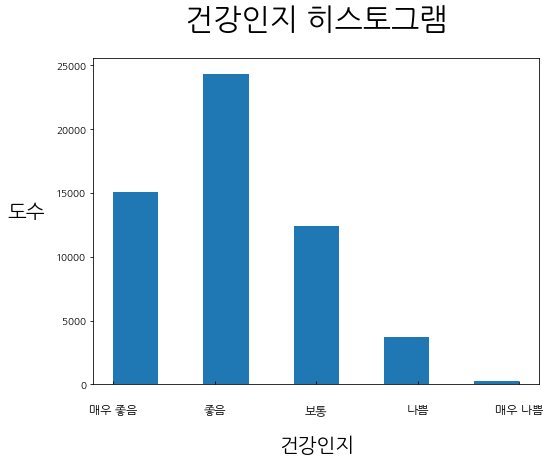
- plt.hist(density=True)로 지정해주면, 빈도가 아닌, 비율로 나타낼 수도 있다.
- 그러나, 이 비율은 히스토그램 전체를 1로 하는 비율이 아닌, 최대 빈도를 1로 하는 비율이다.
fig = plt.figure(figsize=(8, 6))
plt.hist(Rawdata.건강인지.to_numpy(), bins=9, density=True)
plt.xticks(np.arange(1, 6), labels=["매우 좋음", "좋음", "보통", "나쁨", "매우 나쁨"])
plt.tick_params(axis="x", direction="in", labelsize = 12, pad = 20)
plt.title("건강인지 히스토그램", fontsize = 30, pad = 30)
plt.xlabel('건강인지', fontsize = 20, loc = 'center', labelpad = 20)
plt.ylabel('도수', fontsize = 20, rotation = 0, loc='center', labelpad = 30)
plt.show()
- 입력된 데이터는 숫자지만, 실제로는 문자인 Factor이므로, label을 문자로 입력하였다.
>>> Rawdata.건강인지.to_numpy()
array([1., 1., 2., ..., 4., 3., 3.])- 실제 정의에 맞게 하려면, 다음과 같이 숫자를 원래 형태인 문자로 바꿔주고, 문자 배열에 대한 도수를 히스토그램으로 그려야 한다.
건강인지 = Rawdata.건강인지.to_numpy()
건강인지 = np.where(건강인지==1, "매우 좋음",
np.where(건강인지==2, "좋음",
np.where(건강인지==3, "보통",
np.where(건강인지==4, "나쁨", "매우 나쁨"))))
2. 도수분포다각형
- 도수분포다각형은 히스토그램의 각 중간점을 이어서 그린 것으로, 데이터가 연속적인 경우에 사용한다.
- 도수분포다각형을 사용하면, 분포의 윤곽이 보다 명확하게 보이며, 빈도의 증감을 보다 명확히 볼 수 있다.
- 또한, 서로 다른 집단에 대한 도수분포를 같은 그림 위에서 비교할 수 있다는 장점이 있다.
- 도수분포다각형, 누적도수분포곡선은 도수분포표를 기반으로 그리는 것이 훨씬 쉽다(히스토그램 역시, 이미 생성된 도수분포표를 기반으로 막대그래프로 그리는 것이 추가 연산 시간이 없으므로 쉽다).
- 이전 포스트에서 만들었던, 16세 남성의 키와 16세 여성의 키를 10cm 간격으로 범주화한 도수분포표를 대상으로 해서 만들어보도록 하자.
- 총합은 도수분포표를 이해하기 좋게 만든 것이므로, 제거하고, 필요한 각 클래스별 값만 유지하겠다.
def cat_height(array):
cat_array = np.where(array<=140, "140 이하",
np.where((array>140) & (array<=150), "140~150",
np.where((array>150) & (array<=160), "150~160",
np.where((array>160) & (array<=170), "160~170",
np.where((array>170) & (array<=180), "170~180",
np.where((array>180) & (array<=190), "180~190", "190 이상"))))))
return cat_array
def Freq_table(array):
freq_table = pd.DataFrame(pd.Series(array).value_counts(), columns=["freq"])
freq_table.sort_index(inplace = True)
freq_table["ratio"] = freq_table.freq / sum(freq_table.freq)
freq_table["cum_freq"] = np.cumsum(freq_table.freq)
freq_table["cum_ratio"] = np.round(np.cumsum(freq_table.ratio), 2)
freq_table["ratio"] = np.round(freq_table["ratio"], 2)
return freq_table
남자_16세_키 = Rawdata[(Rawdata["연령"] == 16) & (Rawdata["성별"] == 1.0)]["키"].to_numpy()
여자_16세_키 = Rawdata[(Rawdata["연령"] == 16) & (Rawdata["성별"] == 2.0)]["키"].to_numpy()
M_DF = Freq_table(cat_height(남자_16세_키))
F_DF = Freq_table(cat_height(여자_16세_키))fig = plt.figure(figsize=(8, 6))
plt.plot(F_DF.index, F_DF.ratio, label = "Female, 16 years old")
plt.plot(M_DF.index, M_DF.ratio, linestyle = "--", label = "Male, 16 years old")
plt.title("16세 남성 & 여성 키 도수분포다각형",fontsize = 20, pad = 20)
plt.xlabel("키", fontsize = 15)
plt.ylabel("비율", fontsize = 15, rotation = 0, labelpad = 30)
plt.legend(loc="upper right")
plt.show()
- 생성된 두 집단의 도수분포표를 상대적으로 비교하기 위해, 상대 빈도인 비율을 사용하여 그래프를 그렸다.
- 도수분포다각형이 히스토그램의 꼭짓점을 연결한 것임을 보기 위해 히스토그램도 뒤에 연하게 그려보자.
fig = plt.figure(figsize=(8, 6))
plt.plot(F_DF.index, F_DF.ratio, label = "Female, 16 years old")
plt.plot(M_DF.index, M_DF.ratio, linestyle = "--", label = "Male, 16 years old")
plt.bar(F_DF.index, F_DF.ratio, alpha = 0.4, color = "blue")
plt.bar(M_DF.index, M_DF.ratio, alpha = 0.4, color = "yellow")
plt.title("16세 남성 & 여성 키 도수분포다각형",fontsize = 20, pad = 20)
plt.xlabel("키", fontsize = 15)
plt.ylabel("비율", fontsize = 15, rotation = 0, labelpad = 30)
plt.legend(loc="upper right")
plt.show()
- 동일한 비율을 사용하기 위해 plt에서 histogram 함수가 아닌 막대그래프인 bar를 가지고 왔다.
- 히스토그램과 막대그래프는 본질이 다르지만, 도수분포표를 사용해서 그린다면 히스토그램과 막대그래프는 동일한 결과를 가지고 온다.
(히스토그램은 데이터가 한 차원만 들어가고, 그 빈도로 그래프를 그린다. 막대그래프는 두 차원의 데이터가 필요하며, 그 두 차원의 데이터를 이용해서 그래프를 그린다) - 가지고 있는 전체 데이터를 이용해서 그래프를 그린다면 히스토그램을 사용하고, 이미 도수분포표를 만들었다면, 막대그래프를 그리길 추천한다.
3. 누적도수분포곡선
- 누적도수분포곡선은 위에서 도수분포다각형을 그렸던 방법에서, y축에 들어가는 데이터만 누적 도수로 바꾸면 된다.
- 이번에도 두 집단을 비교하기 쉽도록, 비율로 구해보도록 하겠다.
fig = plt.figure(figsize=(8, 6))
plt.plot(F_DF.index, F_DF.cum_ratio, label = "Female, 16 years old")
plt.plot(M_DF.index, M_DF.cum_ratio, linestyle = "--", label = "Male, 16 years old")
plt.bar(F_DF.index, F_DF.cum_ratio, alpha = 0.4, color = "blue")
plt.bar(M_DF.index, M_DF.cum_ratio, alpha = 0.4, color = "yellow")
plt.title("16세 남성 & 여성 키 누적도수분포곡선",fontsize = 20, pad = 20)
plt.xlabel("키", fontsize = 15)
plt.ylabel("비율", fontsize = 15, rotation = 0, labelpad = 30)
plt.legend(loc="lower right")
plt.show()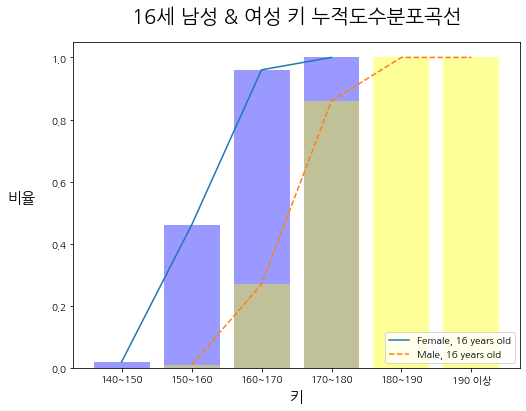
지금까지 파이썬을 사용해서 도수분포표의 시각화를 해보았다. 개인적으로는 도수분포표를 먼저 구하고, 그 도수분포표를 바탕으로 시각화를 진행하길 바란다.
728x90
반응형
'Python으로 하는 기초통계학 > 기본 개념' 카테고리의 다른 글
| 중심경향치(2) - 산술 평균, 기하 평균, 조화 평균, 모평균과 표본 평균이 같은 이유 (0) | 2021.03.03 |
|---|---|
| 중심경향치(1) - 최빈값, 중앙값 (0) | 2021.03.03 |
| 도수분포표 (0) | 2021.03.02 |
| 통계 분석을 위한 데이터 준비 (0) | 2021.03.01 |
| 변수(Variable) (0) | 2021.03.01 |