만년필잉크의 데이터 분석 지식 저장소

 이전 포스트에서 모델을 생성해보고, 생성된 모델의 정보를 살펴보았다. 이번 포스트에서는 모델을 컴파일에 대해 학습해보도록 하겠다.

모델 컴파일

0. 이전 코드 정리

# Import Module
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.layers import (Dense, BatchNormalization, Dropout, Flatten)
from tensorflow.keras.datasets.mnist import load_data

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# Dataset 준비
(train_images, train_labels), (test_images, test_labels)= load_data()

# 무작위로 샘플 추출
np.random.seed(1234)
index_list = np.arange(0, len(train_labels))
valid_index = np.random.choice(index_list, size = 5000, replace = False)

# 검증셋 추출
valid_images = train_images[valid_index]
valid_labels = train_labels[valid_index]

# 학습셋에서 검증셋 제외
train_index = set(index_list) - set(valid_index)
train_images = train_images[list(train_index)]
train_labels = train_labels[list(train_index)]

# min-max scaling
min_key = np.min(train_images)
max_key = np.max(train_images)

train_images = (train_images - min_key)/(max_key - min_key)
valid_images = (valid_images - min_key)/(max_key - min_key)
test_images = (test_images - min_key)/(max_key - min_key)

# 모델 생성
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28], name="Flatten"))
model.add(Dense(300, activation="relu", name="Hidden1"))
model.add(Dense(200, activation="relu", name="Hidden2"))
model.add(Dense(100, activation="relu", name="Hidden3"))
model.add(Dense(10, activation="softmax", name="Output"))

1. 모델 컴파일

# 모델 컴파일
opt = keras.optimizers.Adam(learning_rate=0.005)
model.compile(optimizer = opt,
              loss = "sparse_categorical_crossentropy",
              metrics = ["accuracy"])

• 모델을 어떤 방식으로 학습시킬지 결정하는 과정이다.
• 모델 컴파일에서 지정하는 주요 항목은 최적화 방법인 옵티마이저(Optimizer)와 손실 함수(loss)이다.
• 추가로, 훈련과 평가 시 계산할 지표를 추가로 지정할 수 있다(metrics).

2. Optimizer

• 최적화 방법인 Optimizer는 경사 하강법(GD)을 어떤 방법으로 사용할지를 정한다고 생각하면 된다.
• Optimizer를 정하는 이유는 Optimizer 방법을 무엇을 선택하느냐에 따라 최적해를 찾아가는 속도가 크게 달라진다.
• 경사 하강법(GD)은 기본적으로 4가지 문제가 존재하며, 이는 다음과 같다.
  (좀 더 자세히 알고 싶은 사람은 다음 포스팅: "머신러닝-6.1. 최적화(2)-경사하강법의 한계점"을 참고하기 바란다.)

1. 데이터가 많아질수록 계산량이 증가함
2. Local minimum 문제
3. Plateau 문제
4. Zigzag 문제

• 위 문제들을 간단하게 말하면, 경사 하강법이 가진 구조적 단점으로 인해, 최적해를 제대로 찾아가지 못하거나, 찾는 속도가 늦어진다는 것이다.
• 이를 해결하기 위해선 데이터셋에 맞는 Optimizer를 사용해야 하며, 단순하게 가장 많이 사용하는 Optimizer가 Adam이므로, Adam을 사용하는 것은 그다지 추천할 수 없는 방법이다.

# Optimizer는
model.compile(optimizer = "Adam",
              loss = "sparse_categorical_crossentropy",
              metrics = ["accuracy"])

• 위 방법으로 Optimizer를 하게 되면, 코드는 단순하지만, 학습률, Momentum과 같은 Optimizer 고유의 하이퍼 파라미터를 수정할 수 없다. 

# 모델 컴파일
opt = keras.optimizers.Adam(learning_rate=0.005)
model.compile(optimizer = opt,
              loss = "sparse_categorical_crossentropy",
              metrics = ["accuracy"])

• 위 방법으로 Optimizer를 잡아줘야, 각종 하이퍼 파라미터를 수정할 수 있다.
• keras.optimizers. 뒤에 원하는 optimizer를 넣으면 된다.

3. Optimizer의 종류

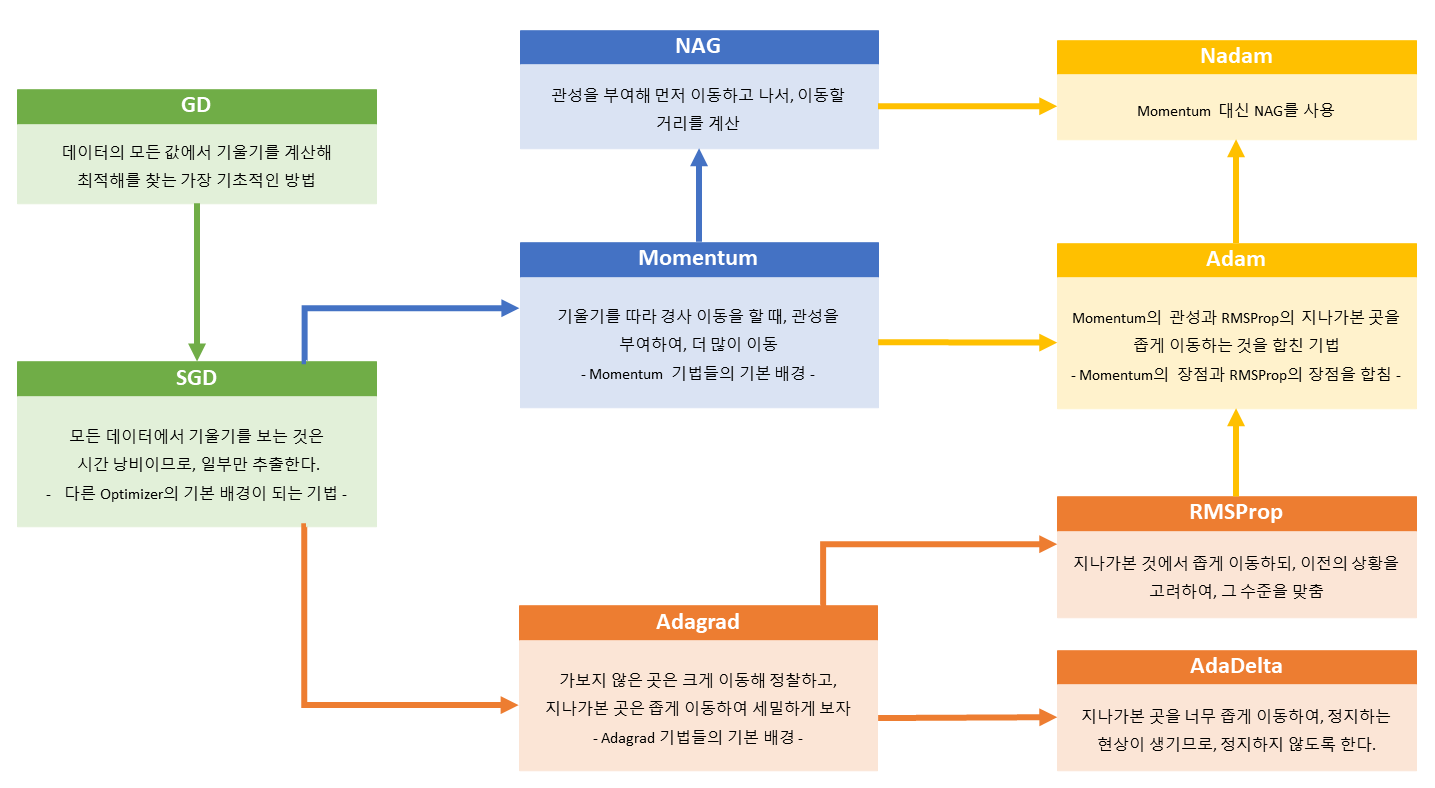
• Optimizer는 기본적으로 SGD를 기반으로 하므로, 확률적 추출을 통해 경사 하강법을 시행한다.
• Optimizer는 크게 Momentum 방식(관성 부여)과 Adagrad 방식(상황에 따른 이동 거리 조정)으로 나뉜다.
• Momentum 방식과 Adagrad 방식을 하나로 합친 방법이 Adam과 Nadam이다.
• 다른 Optimizer를 사용함으로 인해 최적해를 찾아가는 방법이 달라지게 되고, 그로 인해 학습 속도가 바뀌게 된다.
• Local minimum 문제는 무작위 가중치 초기화로 인해 발생할 가능성이 매우 낮다.
• 단순하게 Adam만 고집하지 말고, 여러 Optimizer를 사용하길 바란다.
• Optimizer와 경사하강법에 대한 상세한 설명을 보고자 한다면, 다음 포스트를 참고하기 바란다.
• 참고: "머신러닝-6.0. 최적화(1)-손실함수와 경사하강법"

Optimizer별 최적해 수렴 속도 차이

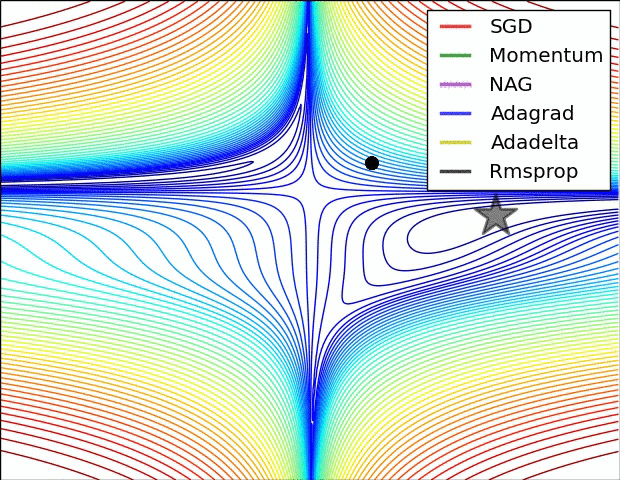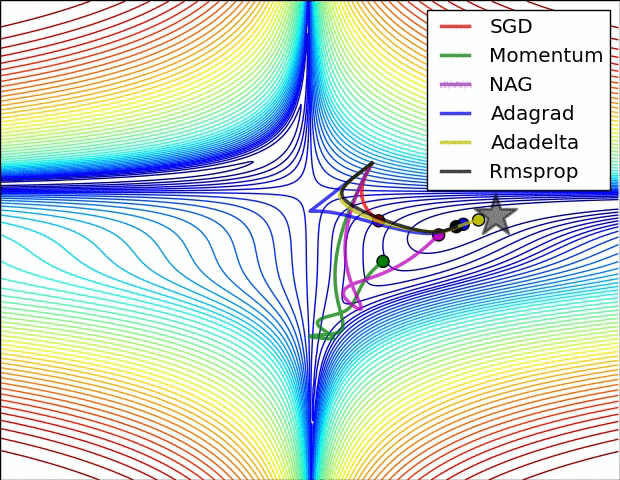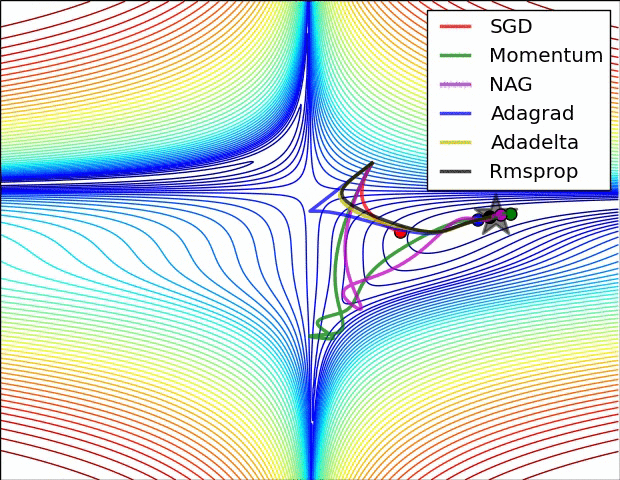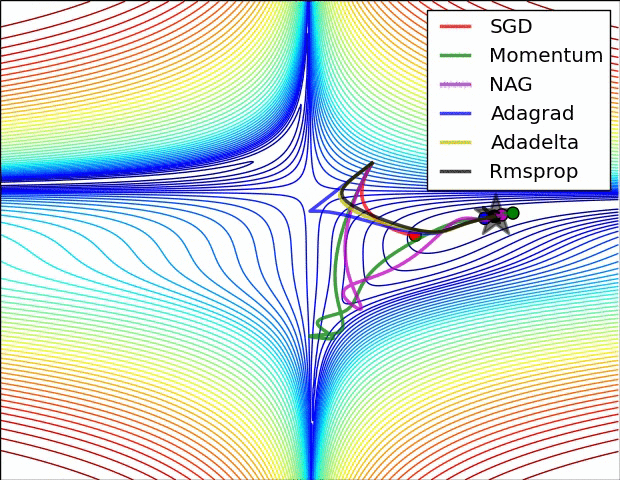
• 별이 최적해라고 할 때, 각종 Optimizer가 최적해를 찾아가는 방식을 시각화한 것이다.
• 해가 n개이므로, 파라미터는 평면이 아니라 입체이며, 이 입체를 이해하기 쉽도록 2차원 등고선으로 그린 것이다.

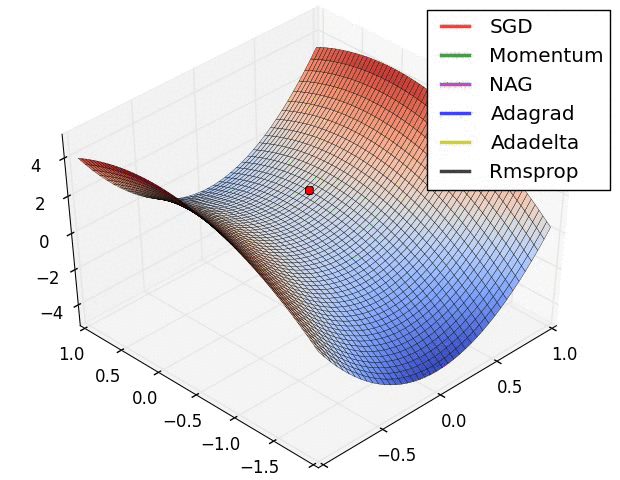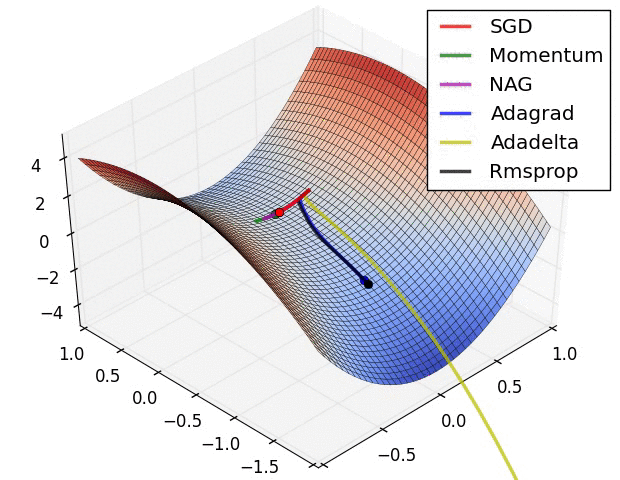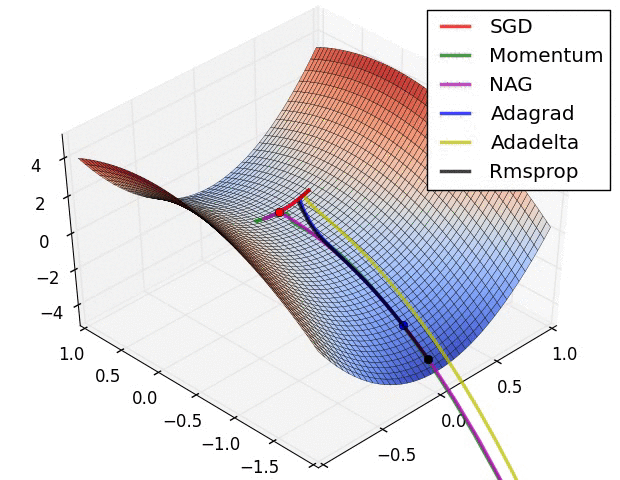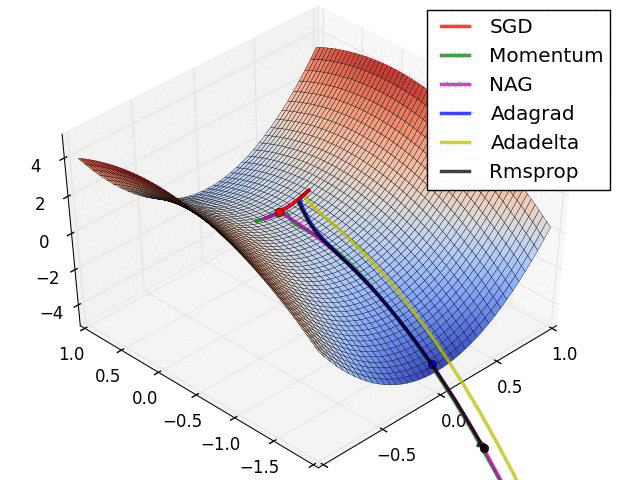
• 말안장 그림이라 하여, 3차원으로 최적해를 찾아가는 과정을 그린 것이다.
• SGD는 지역 최솟값(Local minimum)에 빠져 최적해를 찾아가지 못하였다.
• 위 두 그림의 출처는 다음과 같으며, 보다 자세한 설명을 보고 싶은 경우 해당 사이트를 참고하기 바란다.
• ruder.io/optimizing-gradient-descent/

4. loss

• 손실 함수는 데이터셋과 라벨 데이터의 생김새에 따라 사용하는 방법이 달라진다.
• 기본적으로 연속형 데이터를 대상으로는 제곱 오차(SE)에서 파생된 기법을 사용하며, 범주형 데이터를 대상으로는 크로스 엔트로피 오차(CEE)에서 파생된 기법을 사용한다.
• 클래스의 수나 Label의 형태에 따라 사용하는 방법이 조금씩 달라진다.
• 가장 많이 사용되는 손실 함수의 사용 예는 다음과 같다.

• 위 표는 기본적인 손실 함수에 대한 것이므로, 성능이 나오지 않는다면, 다른 손실 함수를 사용할 필요가 있다.
• 위 손실함수에 대한 상세한 설명을 보고자 한다면, 아래 포스팅을 참고하기 바란다.
• 참고: "머신러닝-5.0. 손실함수(1)-제곱오차(SE)와 오차제곱합(SSE)
• 모든 손실 함수의 목록은 아래 주소에 있으므로 필요시, 참고하기 바란다.
• www.tensorflow.org/api_docs/python/tf/keras/losses

5. metrics

• 평가 기준으로 모델의 학습에는 영향을 미치지 않으나, 학습 중에 제대로 학습되고 있는지를 볼 수 있다.
• metrics에 무엇을 넣느냐에 따라 학습 시, 히스토리에 나오는 출력 Log가 달라지게 된다.
• 일반적으로 accuracy 즉, 정확도가 사용된다.
• 이 역시 데이터 셋에 따라 바뀌며, 손실 함수와 유사한 것을 선택하면 된다.
• metrics에 사용하는 하이퍼 파라미터는 아래 사이트를 참고하기 바란다.
• keras.io/api/metrics/

 지금까지 Compile을 하는 방법에 대해 알아보았다. Compile은 일반적으로 사용하는 기법을 사용하여도 큰 차이를 느끼지 못할 수도 있으나, 제대로 모델을 학습시키기 위해선 데이터의 형태에 맞는 하이퍼 파라미터를 잡아주는 것이 좋다.

 다음 포스트에서는 모델을 실제로 학습시켜보고, 그 Log를 시각화하여 최적의 Epochs을 선택하는 방법에 대해 학습해보겠다.

 지금까지 가중치를 평가하는 방법인 손실함수(Loss Function)에 대해 학습해보았다. 그렇다면, 어떻게 손실함수를 기반으로 최적의 가중치를 찾아낼까?

 이번 포스트에서는 손실함수로부터 어떻게 경사 하강법이 나오게 되었는지를 이야기해보고, 경사하강법을 위주로 설명해보도록 하겠다.

손실함수와 경사하강법

1. 최적화(Optimizer)

• 최적화는 손실함수(Loss Function)의 결과값을 최소화하는 가중치를 찾아내는 것이 목적이다.
• 그렇다면, 손실함수의 개형은 어떻게 생겼을까?
• 예상한 값과 실제값의 차이인 제곱 오차(SE)를 가지고, 손실함수의 개형을 보도록 하자.

$$ SE = (y - \hat{y})^2 $$

• 이해하기 쉽도록 예측값을 변수(가중치)가 1개만 있는 퍼셉트론을 가져와보자
• 예측값은 선형이다(변수는 가중치인 $w$이며, $x$와 상관 없이, 가산성과 동차성이 성립한다.)

$$ \hat{y} = wx + b $$

• 제곱 오차의 $\hat{y}$에 예측값을 대입하고 식을 풀어보자.

$$ (y - \hat{y})^2 = (y - (wx + b))^2 = y^2 -2y(wx + b) + (wx + b)^2 = w^2x^2 + 2wxb + b^2 - 2wxy - 2yb + y^2 $$

• 위 식에서 변수는 $w$이므로, 위 함수는 1개의 최적해를 갖는 이차 함수 형태인 것을 알 수 있다.
• 그러므로, 손실함수의 개형은 다음과 같다.

2. 경사하강법(Gradient Descent)

• 경사 하강법은 1차 미분계수를 이용해 함수의 최소값을 찾아가는 방법으로, 함수 값이 낮아지는 방향으로 독립 변수 값을 변형시켜가면서 최종적으로 최소 함수 값을 갖도록 하는 독립 변수 값을 찾는 방법이다.
• 위에서 보듯, 손실함수의 개형은 1개의 최적해를 갖는 2차 함수의 형태이므로, 경사하강법을 사용하여, 최소 함수 값을 갖도록 하는 최적해(가중치)를 탐색해야한다.
• 경사 하강법은 임의의 가중치를 설정하여, 그 점에서의 기울기를 계산하고, 그 기울기를 힌트로 기울기가 0인 지점을 찾아간다.
• 손실 함수의 부호를 반전시켜, 최댓값을 찾는다면 경사 상승법(Gradient Ascent)이 되나, 동일한 것이므로, 굳이 사용하지 않는다.

• 위 그럼처럼 기울기는 손실함수에서 임의의 가중치에서 시작하며, 기울기가 음수인 경우에는 양의 방향으로 이동하고, 기울기가 양수인 경우에는 음의 방향으로 이동하여, 극솟값을 찾아간다.
• 여기서 움직이는 기울기(경사)는 가중치에 대하여 편미분 한 벡터이고, 이 가중치를 조금씩 움직인다.

3. 경사하강법 공식

• 경사 하강법을 공식으로 써보면 다음과 같다.

$$ x_{i+1} = x_i - \eta\bigtriangledown f(x_i) $$

• 여기서 $\eta$(eta, 에타)는 학습률(Learning Rate)이라 하며, 한 번의 학습에서 얼마나 이동할지를 정한다.
• $\bigtriangledown$는 벡터 미분 연산자로 델(del) 연산자라 하며 이 기호를 나블라(nabla) 기호라고 한다.
• 스칼라 함수 $f(x)$의 기울기는 $\bigtriangledown f$로 표현한다.
• 기울기는 $f$의 각 성분의 편미분으로 구성된 열 벡터로 정의하고, 아래와 같이 표시한다.

$$ \bigtriangledown f = (\frac{\partial f}{\partial x_1}, ..., \frac{\partial f}{\partial x_n}) $$

$$ \bigtriangledown f = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}) $$

• 예를 들어 함수 $f(x, y, z) = 2x + 3y^2 - sin(z)$의 기울기는 다음과 같다.

$$ \bigtriangledown f = (\frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} + \frac{\partial f}{\partial z}) =(2, 6y, -coas(z)) $$

• ko.wikipedia.org/wiki/%EA%B8%B0%EC%9A%B8%EA%B8%B0_(%EB%B2%A1%ED%84%B0)

• 즉, 경사하강법 공식은 현재의 위치 $x_i$에 학습률 $\eta$에 그 위치에서의 기울기 $\bigtriangledown f(x_i)$만큼을 곱한 값을 뺀만큼 위치를 이동시켜 다음 위치 $x_{i+1}$로 이동한다는 소리다.
• 여기서 학습률과 기울기 곱($\eta\bigtriangledown f(x_i)$)을 빼는 이유는 현재의 기울기의 반대방향으로 이동하여, 극소값에 도달하기 위해서이다.

4. 학습률(Learning Rate, LR)

4.1. 경사 하강법 공식에서의 학습률의 영향

• 위 경사 하강법의 공식에서 중요한 것은 학습률(Laerning Rate)인데, 이 학습률에 따라 경사 하강법 시, 이동하는 수준이 달라지게 된다.
• 예를 들어, 기울기가 2.5이고 학습률이 0.01이라면, 경사하강법 알고리즘은 이전 지점으로부터 0.025 떨어진 지점을 다음 지점으로 결정한다.
• 즉, "이동 거리 = 학습률 X 기울기"로 움직인다. 이는 기울기가 낮다면 학습률이 높다할지라도 움직이는 거리가 줄어든다는 소리이고, 큰 고랑에 빠진다면, 거기서 나오지 못하고 수렴할 수 있다는 소리다.

4.2. 학습률이 낮은 경우

• 학습률이 낮다면, 이동하는 거리가 짧으며, 경사하강법 공식에 의해 이동할수록 기울기가 더욱 감소하므로, 짧은 이동 거리가 더 짧아진다.
• 그로 인해, 경사 하강법 알고리즘이 수렴하기 위해 반복해야하는 데이터 양이 많아지므로, 학습 시간이 늘어나게 된다.

4.3. 학습률이 높은 경우

• 학습률이 지나치게 큰 경우, 크게 이동하므로, 수렴이 빨리 발생해 학습 시간이 적게 걸린다.
• 그러나, 너무 크게 이동하므로, 전역 최솟값(Global minimum)이 있는 영역을 건너 뛰어 지역 최솟값에서 수렴할 수도 있다.
  (이 부분은 다음 포스트에서 세세하게 다루도록 하겠다.)

 지금까지 손실함수를 최소화하는 방법으로 어째서 경사하강법을 사용하는지와 경사하강법이 어떠한 구조로 움직이는지에 대하여 학습해보았다.

 다음 포스트에서는 경사하강법의 한계점에 대해 학습해보도록 하겠다.

 이전 포스트에서는 범주형 데이터를 분류하는데 주로 사용되는 손실함수인 교차 엔트로피 오차와 그 근간이 되는 정보 이론에서의 엔트로피가 무엇인지를 알아보았다.

 이번 포스트에서는 교차 엔트로피 오차 중에서도 이진 분류를 할 때, 주로 사용되는 이진 교차 엔트로피 오차에 대해 학습해보도록 하겠다.

이진 교차 엔트로피 오차(Binary Cross Entropy Error)

• 교차 엔트로피 오차는 나누고자 하는 분류가 몇 개인지에 따라 사용하는 손실함수가 바뀌게 된다.
• 이는 사용되는 활성화 함수가 다르기 때문으로, 범주가 2개인 데이터는 시그모이드(Sigmoid) 함수를 사용하여 0~1 사이의 값을 반환하거나, 하이퍼볼릭 탄젠트(Hyperbolic Tangent) 함수를 사용하여 -1~1 사이의 값을 반환한다. 이 두 활성화 함수 모두 출력값이 단 하나의 스칼라 값이다.
• 반면에 범주가 3개 이상이라면, 총 합 1에 각 클래스에 속할 확률을 클래스의 수만큼 반환하는 소프트맥스(Softmax) 함수를 사용하여 클래스 수만큼의 원소가 들어있는 배열을 반환하므로, 이에 대한 평가 방법이 달라져야 한다.
• 이진 교차 엔트로피 오차는 로그 손실(Log loss) 또는 로지스틱 손실(Logistic loss)라 불리며, 주로 로지스틱 회귀의 비용 함수로 사용된다.

1. 이진 교차 엔트로피 오차의 공식

• 이진 교차 엔트로피 오차의 공식은 다음과 같다.

$$ Loss = -\frac{1}{N}\sum_{i=1}^{N}(y_i*ln\hat{y_i} + (1-y_i)*ln(1-\hat{y_i})) $$

• $\hat{y_i}$는 예측값이며, $y_i$는 실제값이다.
• 얼핏 보면, 꽤 어려워보이는데 앞서 우리가 학습했던 내용을 기반으로 보면 상당히 단순한 공식이다.
• 먼저 앞서 학습헀던 공식들을 조금 더 이해해보자.
• 엔트로피 공식은 다음과 같다.

$$H(X) = - \sum_{x}P(x)lnP(x) $$

• 교차 엔트로피 공식은 다음과 같다. 

$$H(P, Q) = - \sum_{x}P(x)lnQ(x) $$

• 위 두 공식에서 엔트로피 공식과 교차 엔트로피 공식의 차이는 실제값($P(x)$)과 타깃이 되는 예측값($Q(x)$)의 정보량 비율 합으로 구해지는 것을 알 수 있다.
• 여기서, 교차 엔트로피 오차는 분류할 클래스의 수가 $N>2$인 정수이므로, 클래스별 확률이 다 달랐으나, 이진 교차 엔트로피 오차는 클래스가 "y=0"와 "y=1" 단 두 가지만 존재하는 것을 알 수 있다.

$$ p = [y, 1-y] $$

$$ q = [\hat{y}, 1-\hat{y}] $$

• 그렇다면, $y=0$의 교차 엔트로피 공식을 만들어보자.

$$ H(y)= -\sum_{i=1}^{N}(y_i*ln\hat{y_i}) $$

• $y=1$의 교차 엔트로피 공식을 만들어보자.

$$ H(y-1)= -\sum_{i=1}^{N}((1-y_i)*ln(1-\hat{y_i})) $$

• 밑과 위가 같은 시그마끼리는 서로 합칠 수 있다.

$$ H(y) + H(y-1)= -\sum_{i=1}^{N}(y_i*ln\hat{y_i} + (1-y_i)*ln(1-\hat{y_i})) $$

• 여기서 $N$개의 학습 데이터 전체에 대한 교차 엔트로피를 구해주는 것이므로, 평균으로 만들어 값을 줄여주자!

$$ Loss = -\frac{1}{N}\sum_{i=1}^{N}(y_i*ln\hat{y_i} + (1-y_i)*ln(1-\hat{y_i})) $$

• 앞서, 오차제곱합(SSE)와 평균제곱오차(MSE)에 대해 보았을 텐데, 합은 데이터의 수가 많아질수록 증가하므로, 데이터의 수로 나눠 평균으로 만들어야 이를 보정해줄 수 있다.
• 여기서 데이터의 수는 입력 값의 벡터 크기가 아니라, Input되는 데이터의 수를 말한다.
• 이진 교차 엔트로피 오차는 출력층의 노드 수를 하나로 하여 출력값을 하나로 받으므로, 실제값(Label)과 예측값(predict) 모두 하나의 스칼라 값이다.
• 왜 교차 엔트로피 오차(CEE)에서는 왜 N으로 나눠주지 않았는지 의문이 들 수 있는데, 그 이유는 교차 엔트로피 오차는 하나의 데이터에 대해서만 실시한 것이기 때문이다.
• 교차 엔트로피 오차(CEE)를 N개의 데이터에 대해 실시하면 범주형 교차 엔트로피 오차(Categorical Cross Entropy Error)가 된다.

2. 구현해보자!

• 이진형 교차 엔트로피 에러(BCEE)는 앞서 학습 했던, 교차 엔트로피 에러와 꽤 유사하다.

>>> import numpy as np

>>> def BCEE(predict, label):
    
>>>     delta = 1e-7
>>>     pred_diff = 1 - predict
>>>     label_diff = 1 - label
>>>     result = -(np.sum(label*np.log(predict+delta)+label_diff*np.log(pred_diff+delta)))/len(label)
    
>>>     return result

>>> predict = np.array([0.8, 0.1, 0.05, 0.9, 0.05])
>>> label = np.array([1, 0, 0, 1, 0])
>>> BCEE(predict, label)
0.10729012273129139

• 위 데이터를 보면 총 5개의 데이터 셋에 대한 이진 분류 결과를 보았다.
• 이번에는 예측값과 실제 데이터를 더 유사하게 하여 결과를 내보자.

>>> predict = np.array([0.95, 0.05, 0.01, 0.95, 0.01])
>>> label = np.array([1, 0, 0, 1, 0])
>>> BCEE(predict, label)
0.03479600741200121

• 보다 0에 가까워진 것을 알 수 있다.
• 이번에는 좀 멀게 만들어보자.

>>> predict = np.array([0.30, 0.40, 0.20, 0.65, 0.2])
>>> label = np.array([1, 0, 0, 1, 0])
>>> BCEE(predict, label)

 지금까지 이진 교차 엔트로피 오차(Binary Cross Entropy Error, BCEE)에 대해 학습해보았다. BCEE는 앞서 봤던 CEE를 단순하게 "y=0"일 사건과 "y=1"일 사건에 대한 교차 엔트로피 오차 합의 평균을 낸 것으로, 큰 차이가 없다는 것을 알 수 있다.

 다음 포스트에서는 이진 교차 엔트로피 오차에 대응하는 다중 분류에 사용되는 범주형 교차 엔트로피 오차(Categorical Cross Entropy Error)에 대해 학습해보도록 하겠다.