만년필잉크의 데이터 분석 지식 저장소

 이전 포스트에서 Numpy의 array에 대해 간략하게 훑어보았다. 이번 포스트에선 머신러닝에서 대표적으로 사용되는 모듈인 tensorflow의 고유 Type 중 하나인 Tensor에 대해 학습해보겠다.

tensor

개요

• Tensorflow는 Google에서 개발한 머신러닝의 대표적인 모듈로 tensor는 이 tensorflow의 대표적인 Type이지만, 정작 Tensorflow를 이용해서 머신러닝을 할 때에는 사용할 일이 많지 않은 type이기도 하다.
• "Tensorflow를 활용해서 기계학습을 진행하는데 tensor를 쓰지 않는다니??"라는 생각이 들 수 있는데, tensorflow로 기계학습 진행 시, 일반적으로 keras를 이용해서 model을 생성하게 되고, 그 모델에 들어갈 데이터셋의 핸들링 과정에서 tensor로 핸들링하는 것보다 Numpy의 array를 이용해서 핸들링할 일이 더 많기 때문이다.
• 애초에 Tensorflow의 tensor와 Numpy의 array의 관련 함수의 상당수가 거의 유사하다 보니, 여기저기 많이 쓰여 익숙하게 쓰는 Numpy의 array가 더 편하기 때문이기도 하다.

Tensor란?

• Tensor란 N 차원의 배열(array)을 의미한다.
• 일반적으로 1차원 배열을 벡터(Vector), 2차원 배열을 행렬(Matrix), 3차원 이상의 배열을 다차원 배열이라고 하며, 이들 모두를 통틀어서 Tensor라고 한다.
• Tensor는 N 차원 배열이므로, 배열을 다루는 Numpy의 array와 태생적으로 기능이 유사할 수 밖에 없다.

Rank

• 뭔가 대충 설명한 느낌이 강한데, 보다 구체적으로 이해하려면 머릿속에 그림을 그려봐야한다.
• Scalar > Vector > Matrix > 3-Tensor 이런 식으로 하나하나 층을 쌓아보자

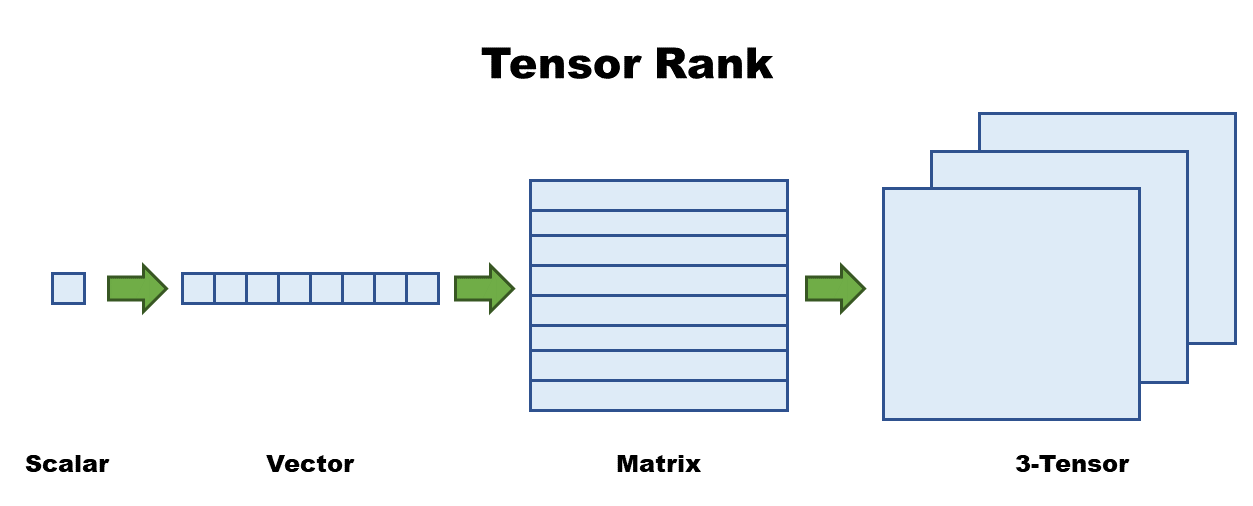
• Scalar를 하나의 원소로 보고, 그 원소가 일렬로 쭉 쌓으면 Vector, 그 Vector를 아래로 쭉 쌓으면 Matrix, Matrix를 N개의 층을 쌓으면 N-Tensor가 되는 것이다.
• 보통 3-Tensor는 그림을 Tensor화(수치화) 했을 때, Red, Green, Blue에 대한 3개의 Layer를 쌓는다. 이를 Channer이라 한다.

Tensor를 가지고 놀아보자

# Tensor를 생성해보자.
# 1. 0으로 채워진 Tensor를 만들어보자
>>> tf.zeros(shape=(3, 10))
<tf.Tensor: shape=(3, 10), dtype=float32, numpy=
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]], dtype=float32)>
       
       
# 2. 1로 채워진 Tensor를 만들어보자
>>> tf.ones(shape=(3,4), dtype = "int16")
<tf.Tensor: shape=(3, 4), dtype=int16, numpy=
array([[1, 1, 1, 1],
       [1, 1, 1, 1],
       [1, 1, 1, 1]], dtype=int16)>
       
       
# 3. 내가 원하는 상수로 채워진 Tensor를 만들어보자 
>>> tf.fill(dims=(3, 6), value=3)
<tf.Tensor: shape=(3, 6), dtype=int32, numpy=
array([[3, 3, 3, 3, 3, 3],
       [3, 3, 3, 3, 3, 3],
       [3, 3, 3, 3, 3, 3]])>
       
     
# 4. array를 만들듯이 Tensor를 만들어보자
>>> tf.constant([[1,3,5,7],[2,4,6,8]])
<tf.Tensor: shape=(2, 4), dtype=int32, numpy=
array([[1, 3, 5, 7],
       [2, 4, 6, 8]])>
       

# 5. array를 이용해서 Tensor를 만들어보자
>>> array1 = np.array([[1, 3, 5, 7], [2, 4, 6, 8]])
>>> tf.constant(array1)
<tf.Tensor: shape=(2, 4), dtype=int32, numpy=
array([[1, 3, 5, 7],
       [2, 4, 6, 8]])>


# 6. 패턴을 갖는 Tensor를 만들어보자
>>> tf.range(1, 20, 3)
<tf.Tensor: shape=(7,), dtype=int32, numpy=array([ 1,  4,  7, 10, 13, 16, 19])>

• 별 설명 없이 여러 tensor를 만들어보았는데, 이를 보면 앞서 봤던 numpy의 array와 굉장히 유사하다는 생각이 들지 않는가?
• 애초에 tf.constant() 함수에 array를 담으면 tensor가 되고 모든 형태의 array를 포함하는 것이 tensor이므로, 굳이 tensor를 공부하지 않아도 Numpy의 array만 잘 다루면 tensor를 무리 없이 쓸 수 있다.

# Tensor의 다양한 속성들을 뽑아보자
>>> TS1 = tf.constant([[1, 3, 5, 7, 9, 11], [2, 4, 6, 8, 10, 12], [2, 3, 5, 7, 11, 13]],
						dtype="float64")
>>> TS1
<tf.Tensor: shape=(3, 6), dtype=float64, numpy=
array([[ 1.,  3.,  5.,  7.,  9., 11.],
       [ 2.,  4.,  6.,  8., 10., 12.],
       [ 2.,  3.,  5.,  7., 11., 13.]])>
   
   
# 1. shape을 뽑아보자 
>>> TS1.shape
TensorShape([3, 6])


# 2. shape을 바꿔보자
>>> tf.reshape(TS1, shape=(2, 9))
<tf.Tensor: shape=(2, 9), dtype=float64, numpy=
array([[ 1.,  3.,  5.,  7.,  9., 11.,  2.,  4.,  6.],
       [ 8., 10., 12.,  2.,  3.,  5.,  7., 11., 13.]])>


# 3. dtype을 뽑아보자
>>> TS1.dtype
tf.float64


# 4. dtype을 바꿔보자
>>> tf.cast(TS1, dtype="int64")
<tf.Tensor: shape=(3, 6), dtype=int64, numpy=
array([[ 1,  3,  5,  7,  9, 11],
       [ 2,  4,  6,  8, 10, 12],
       [ 2,  3,  5,  7, 11, 13]], dtype=int64)>

• 위 예제를 보면 굳이 tensor로 변환을 하지 않고, Numpy로 데이터 핸들링을 하는 것이 더 편하겠다는 생각이 들지 않는가?
• tensor를 통해 사용할 수 있는 함수가 이외에도 수없이 많으나, 이에 시간을 할애하기보다는 scipy, pandas, matplotlib 등 다양한 모듈에서 폭넓게 사용할 수 있는 Numpy를 공부하는 것이 보다 효율적으로 판단되므로, 본 블로그에서는 tensor의 관련 함수는 여기까지만 정리하도록 하고 Numpy를 더 자세히 학습하도록 하겠다.

dtype

• 위 예제를 보면 dtype="int64"와 같이 우리가 기존에 알고 있는 int 뒤에 숫자가 붙어 있는 것을 알 수 있다.
• dtype은 float32, float64, int8, int16, int32, int64, unit8, string, bool 등이 있으며 뒤에 있는 숫자는 bit를 의미한다.
• 종종 앞에 있는 dtype인 float은 일치하지만 bit가 일치하지 않아 오류가 발생하기도 하니, 혹여 dtype error가 뜨는 경우, 이를 확인해보도록 하자.

 지금까지 가볍게 tensor에 대해 학습해보았다. tensor는 Numpy의 array와 기능이 거의 일치하며, tensorflow로 학습을 할 때도 Numpy를 주로 사용하니 더 파고들진 않겠다.

 그러나 위에서 설명한 Tensor Rank 그림은 상당히 중요한 그림이므로, 꼭 숙지하도록 하자.

 지금까지 scalar, list Type에 대해서 알아보았다. 이제 남은 대표적인 Type은 array, tensor, dictionary, DataFrame이 있는데, 이들은 앞서 다뤘던 두 Type에 비해 훨씬 심도 깊은 학습이 필요하므로, 특징만 간략히 설명하고 넘어가겠다.

array

Numpy의 array 

• Python의 단점을 이야기할 때, 흔히들 느린 속도를 꼽는데, 이 이미지를 한 번에 종식시킬 수 있는 것이 바로 Numpy라는 모듈이며, 그 Numpy 모듈의 기본 Type이 바로 array다.
• Numpy는 C언어, Fortran을 기반으로 만들어졌기 때문에 연산 속도가 매우 빠르며, 쉬운 것이 장점인 파이썬으로 구현되어 있기에 C언어를 공부하지 않고도 복잡한 수학 연산 문제를 아주 쉽고 빠르게 접근할 수 있다.
• 특히 데이터 분석가의 친구인 판다스의 단점인 느린 속도를 해결할 수 있기 때문에 데이터 분석을 하고자 한다면, Numpy를 아주 잘 다룰 수 있어야 한다.
• Numpy의 array는 Scipy, tensorflow, sklearn, Matplotlib, Pandas 등 빅데이터 분석에서 필수로 사용되는 모듈을 활용하는 데에 있어 기초가 되어준다.
• 보다 상세한 내용은 추후 Numpy에 대해 자세히 학습할 때 이야기해보도록 하자.

# array를 사용하기 위해선 numpy 모듈을 가지고 와야한다.
>>> import numpy as np

# array는 list를 만들고 np.array() 함수에 넣어서 생성하기도 한다.
>>> a = [1,2,3,4,5]
>>> a_array = np.array(a)
>>> a_array
array([1, 2, 3, 4, 5])

• numpy 모듈을 불러오는 import numpy as np는 "numpy를 수입(import) 해오겠다 np 처럼(as)" 이라고 곧이곧대로 해석해도 된다. 
  1. 이게 파이썬의 대표적인 장점 중 하나로 꼽히는 파이썬 코드가 우리가 실제로 사용하는 언어와 굉장히 가깝다는 것을 보여주는 대표적인 예시중 하나이다.
• np는 numpy의 줄임말이며, Python은 "."을 기준으로 하여, 모듈로부터 하위 함수로 한 단계 한단계 내려가는 형태를 가지고 있다.
  • 즉, np.array()는 numpy 모듈의 array() 함수라는 뜻이다.

# array에 담겨있는 data type(dtype)은 상당히 중요하다.
>>> a_array.dtype
dtype('int32')


# 소수(float)로 구성된 array를 만들어보자
>>> b = np.arange(1, 10, 2, dtype = "float")
>>> b
array([1., 3., 5., 7., 9.])

>>> b.dtype
dtype('float64')

• array.dtype은 array의 data type을 알 수 있다.
• np.arange()은 앞서 list의 range와 비슷한 기능을 하며, array를 바로 생성한다.
• array 내 data를 정수로 입력했다 할지라도 dtype을 "float"으로 지정하면 소수로 생성된다.

array 연산과 Broadcast

# Numpy의 array 연산은 R의 Vector 연산과 굉장히 유사하다.
>>> c = np.array([1, 3, 5, 7, 9])
>>> d = np.array([2, 4, 6, 8, 10])
>>> e = np.array([10, 20])


# 자리수가 동일한 array(vector)끼리는 동일한 위치의 원소끼리 연산이 이루어진다.
>>> print(c+d) 
[ 3  7 11 15 19]
>>> print(c*d)
[ 2 12 30 56 90]
>>> print(c/d)
[0.5        0.75       0.83333333 0.875      0.9]


# 자리수가 동일하지 않은 array(vector)간의 연산은 이루어지지 않는다.
>>> print(c + e)
---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-12-3b9c09c64b20> in <module>
----> 1 print(c + e)

ValueError: operands could not be broadcast together with shapes (5,) (2,) 

• Numpy의 array 연산을 보면 R의 Vector 연산과 꽤 유사한 것을 알 수 있다.
• Numpy의 array는 Tensorflow의 기본 Type인 Tensor와 거의 동일한 개념으로 봐도 문제없다.
  1. Tensor란 다차원 배열(array)을 아우르는 말이며, 이 안에는 1차원 배열인 Vector와 2차원 배열인 Metrics를 포함하는 것이다.
  2. 선형 대수학의 관점에서 접근할 때, array에 보다 익숙해지기 위해 1차원 array는 단순하게 vector로 부르도록 하겠다.
• shape(모양)이 동일하지 않은 array끼리 연산 시, ValueError가 발생한다.

# BroadCast
>>> c
array([1, 3, 5, 7, 9])

>>> c * 2
array([ 2,  6, 10, 14, 18])

>>> c + 2
array([ 3,  5,  7,  9, 11])

>>> c / 2
array([0.5, 1.5, 2.5, 3.5, 4.5])

• 1차원 array에 scalar 값을 연산 시, array의 모든 원소에 scalar값이 연산된다.

# array를 여러개 쌓으면 행렬이 된다.
>>> f = np.array([[1, 3, 5, 7],[2, 4, 6, 8]])
>>> f * 2
array([[ 2,  6, 10, 14],
       [ 4,  8, 12, 16]])
 
 
# 행렬에 대한 Broadcast
>>> f = np.array([[1, 3, 5, 7],[2, 4, 6, 8]])
>>> f * np.array([10, 20, 30, 40])
array([[ 10,  60, 150, 280],
       [ 20,  80, 180, 320]])

• m*n행렬에 대해 스칼라 값을 연산하거나  n*1 벡터를 연산하면 array의 Broadcast와 같은 방식으로 연산이 이루어진다.

#  행렬 곱
>>> f = np.array([[1, 3, 5, 7],[2, 4, 6, 8]])
>>> f * np.array([[10, 10, 10, 10], [20, 20, 20, 20]])
array([[ 10,  30,  50,  70],
       [ 40,  80, 120, 160]])
       

>>> g = np.array([[10,10],[20,20],[30,30],[40,40]])
>>> np.dot(f,g)
array([[500, 500],
       [600, 600]])

• 형태(shape)가 동일한 행렬끼리 *+-/와 같은 연산 수행 시, 동일한 위치에 있는 원소끼리 곱해진다(이는 우리가 일반적으로 아는 행렬곱이 아니다.).
• m*n행렬, n*o행렬과 같이 행렬곱이 가능한 대상을 np.dot(mat1, mat2)을 하는 경우 우리가 아는 행렬곱이 연산된다.

배열의 형태

# array의 shape
>>> vt1 = np.array([1,2,3,4])
>>> vt2 = np.arange(1, 5, 0.1)
>>> mat1 = np.array([[1,3,5,7],[2,4,6,8]])
>>> mat2 = np.array([[1,10],[2,20],[3,30],[4,40]])

>>> print(vt1.shape)
(4,)
>>> print(vt2.shape)
(40,)
>>> print(mat1.shape)
(2, 4)
>>> print(mat2.shape)
(4, 2)


# 형태 변환(reshape)
>>> vt1.reshape((4,1))
array([[1],
       [2],
       [3],
       [4]])
>>> mat2.reshape((2,4))
array([[ 1, 10,  2, 20],
       [ 3, 30,  4, 40]])
       
       
# 평활(Flatten)
>>> mat1
array([[1, 3, 5, 7],
       [2, 4, 6, 8]])
>>> mat1.flatten()
array([1, 3, 5, 7, 2, 4, 6, 8])

>>> mat2
array([[ 1, 10],
       [ 2, 20],
       [ 3, 30],
       [ 4, 40]])
>>> mat2.flatten()
array([ 1, 10,  2, 20,  3, 30,  4, 40])

• 앞서 이야기했던 array의 shape은 Numpy를 다루는 데 있어 필수 사항이며, 나아가 딥러닝을 다루는데 주로 사용되는 모듈인 tensorflow를 사용할 때도 매우 중요하다.
• 상당수의 연산 오류는 shape이나 dtype이 일치하지 않아 발생한다.
• reshape() 함수를 이용해서 array의 형태를 바꿀 수 있다.
• 우리가 일반적으로 2차원으로 아는 행렬은 flatten() 함수를 통해 수월하게 벡터화되며, 이는 텐서플로우 학습 시, 상당히 중요한 내용이다.
  1. 행렬이 1차원 배열로 변환 가능하다는 것은 우리가 아는 2차원으로 알고 있는 행렬은 사실 상 1차원임을 의미한다. 이에 대해선 추후 Numpy를 설명하면서 보다 자세히 짚고 넘어가도록 하겠다.

 Numpy의 핵심 Type인 array는 이를 공부하는 데만 해도 상당한 시간을 투자해야 하기 때문에 이번 포스트에서는 가장 기본적인 array의 성격들만 알아보았다.

 앞서 list를 학습할 때, 발생했던 상당 부분의 list의 한계점으로 여겨졌던 부분들은 array를 통해 대부분 해결 가능하다.

 또 다른 Type인 tensorflow의 tensor는 numpy의 array와 굉장히 유사하며, 함수에 약간의 차이가 있긴하나 거의 동일한 기능들이 존재한다. 또한, tensorflow 학습 시, keras를 위주로 쓰게 되며, 굳이 tensor로 연산하기보다 numpy의 array로 연산하는 것을 추천한다. 

1. tensorflow에서 tensor를 다루는 함수는 numpy의 array를 다루는 함수와 기능이 거의 일치한다. 굳이 tensor를 다루는 함수를 공부하지 않아도 tensorflow를 다루는데 큰 지장이 없다.
2. tensorflow에 대해 추후 학습하겠으나, tensorflow 2.0 version에 들어오며, keras를 주로 활용하여 딥러닝을 실시하게 될 것이다.
3. 상세한 내용은 python-Numpy 카테고리에서 포스팅하도록 하겠다.

이번 포스트에선 배열(Array)에 대해 공부해보자.

배열(Array)

: 행렬이 2차원의 데이터라면 배열(Array)는 다차원의 데이터라고 할 수 있다. 예를 들어 2x3 차원의 데이터를 행렬로 표현한다면, 2x3x4 차원의 데이터는 배열(Array)로 표현한다.

• 간단히 말하자면 (NxM)행렬을 Z개 쌓아놓는다고 보면된다.
• 당연히 Z개 쌓여있는 행렬들의 형태(차원)은 모두 동일하다고 할 수 있다.
• array()
  : 배열을 만들 수 있다.
• 주요 Parameter
  : array(data, dim = c(행의 수, 열의 수, 행렬의 수), dimnames = list(c(행의 이름), c(열의 이름), c(행렬의 이름)))

# 배열을 만들어보자.
Vt = seq(from = 1, by = 2, length.out = 12*3)
Ar = array(Vt, dim = c(4, 3, 3), dimnames = list(c("r1", "r2", "r3", "r4"),c("c1", "c2", "c3"),c("M1", "M2", "M3")))
Ar

## , , M1
## 
##    c1 c2 c3
## r1  1  9 17
## r2  3 11 19
## r3  5 13 21
## r4  7 15 23
## 
## , , M2
## 
##    c1 c2 c3
## r1 25 33 41
## r2 27 35 43
## r3 29 37 45
## r4 31 39 47
## 
## , , M3
## 
##    c1 c2 c3
## r1 49 57 65
## r2 51 59 67
## r3 53 61 69
## r4 55 63 71

• 배열은 기본적으로 행렬이 한 열씩 채워가는 방식으로 생성된다.
• 배열 역시 행렬과 마찬가지로, 배열을 구성할 벡터의 원소 수가 배열에 필요한 원소 수보다 작은 경우, 벡터의 앞부분부터 행렬의 빈자리에 구성된다.

배열에서 원하는 데이터 가지고 오기.

• 배열에서 원하는 데이터를 가지고 오는 것은 행렬과 기본적으로 동일하며, 차원이 한 개 더 증가한 것과 같다.

Ar[,,"M2"]

##    c1 c2 c3
## r1 25 33 41
## r2 27 35 43
## r3 29 37 45
## r4 31 39 47

배열은 행렬을 다차원으로 담을 수 있는 데이터 타입으로, 전통적인 통계 분석에서는 그다지 필요가 없어보일 수 있다. 그리고, 동일한 2차원의 행렬에 대해서만 array에 적재할 수 있으므로, 모든 형태의 데이터 타입을 담을 수 있는 List에 비해 그 기능이 부족해보일 수 있다.

그러나, 반대로 말하자면 다차원 행렬을 적극적으로 사용해야하는 공학이나 요즘 핫한 빅데이터 분석에서는 array가 매우 유용한 데이터 타입이라고 할 수 있다. 꼭 숙지해놓고, 잘 활용해보도록 하자.

다음 포스트에서는 R 데이터 타입의 꽃인 데이터 프레임에 대해 학습해보도록 하자.