만년필잉크의 데이터 분석 지식 저장소

 이전 포스트에서 타이타닉 데이터가 어떻게 구성되어 있는지 확인해보았다. 이번 포스트에서는 타이타닉 데이터를 전처리해보고, 생존자 분류 모델을 만들어보자.

타이타닉 데이터 생존자 분류 모델 만들기

• 모든 데이터 분석에서도 그렇듯 딥 러닝 모델 생성에서도 제일 우선 되는 것은 데이터 전처리다.
• 머신러닝 모델을 만들 때의 순서는 다음과 같다.

1. 데이터 셋의 특징을 잘 나타낼 수 있게 전처리를 한다(Data Handling).
2. 학습이 제대로 되도록 데이터 셋을 잘 쪼갠다(Train, Validation, Test).
3. 목적과 데이터에 맞는 모델을 생성한다.
4. 학습 후, 모델의 성능을 평가하고, 성능을 업그레이드한다.

• 이번엔 각 영역이 미치는 영향이 얼마나 큰지를 시각적으로 보도록 하겠다.

0. 데이터 불러오기

• 이전 포스트에서 만들었던 데이터를 가져오는 코드를 정리해보자.

# Import Module
import pandas as pd
import numpy as np
import os
from tensorflow.keras.layers import Dense
from tensorflow import keras

# 모든 Data를 DataFrame의 형태로 dictionary에 넣어 가지고 온다.
def import_Data(file_path):

    result = dict()
    for file in os.listdir(file_path):

        file_name = file[:-4]
        result[file_name] = pd.read_csv(file_path + "/" + file)

    return result

# 해당 경로에 있는 모든 파일을 DataFrame으로 가지고 왔다.
file_path = "./Dataset"
Rawdata_dict = import_Data(file_path)

1. 데이터 전처리

• 이전 포스트에서 파악한 데이터 셋의 내용을 기반으로, 데이터 셋을 전처리해보자.

1.1. 데이터 셋 전처리가 쉽도록 한 덩어리로 만들자.

# 흩어져 있는 데이터를 모아 하나의 Rawdata로 만든다.
def make_Rawdata(dict_data):

    dict_key = list(dict_data.keys())
    test_Dataset = pd.merge(dict_data["gender_submission"], dict_data["test"], how='outer', on="PassengerId")
    Rawdata = pd.concat([dict_data["train"], test_Dataset])
    Rawdata.reset_index(drop=True, inplace=True)
    
    return Rawdata

• pd.merge(): 두 DataFrame을 동일한 Column을 기준(열 기준)으로 하나로 합친다.
• pd.concat(): 모든 Column이 동일한 두 DataFrame을 행 기준으로 하나로 합친다.
• DataFrame.reset_index(): DataFrame의 index를 초기화한다.

Rawdata = make_Rawdata(Rawdata_dict)
Rawdata

1.2. 불필요한 Column을 제거하자.

• 생존 여부에 절대 영향을 줄 수 없는 Column을 제거하여, Feature가 두드러지도록 만들자.
• 고객의 ID(PassengerId), 고객의 이름(Name), 티켓 번호(Tiket)는 생존 여부에 영향을 줄 가능성이 거의 없다고 판단된다. 그러므로, Dataset에서 제거하자.

from copy import copy

def remove_columns(DF, remove_list):
    
    # 원본 정보 유지를 위해 copy하여, 원본 Data와의 종속성을 끊었다.
    result = copy(Rawdata)

    # PassengerId를 Index로 하자.
    result.set_index("PassengerId", inplace = True)

    # 불필요한 column 제거
    for column in remove_list:

        del(result[column])
        
    return result

• copy(Data): Data를 복사하여, 데이터의 종속성이 없는 데이터를 만들어낸다.
• DataFrame.set_index(): 특정 column을 Index로 설정한다.
• del(DataFrame[column]): DataFrame에서 해당 column을 제거한다.

remove_list = ["Name", "Ticket"]
DF_Hand1 = remove_columns(Rawdata, remove_list)
DF_Hand1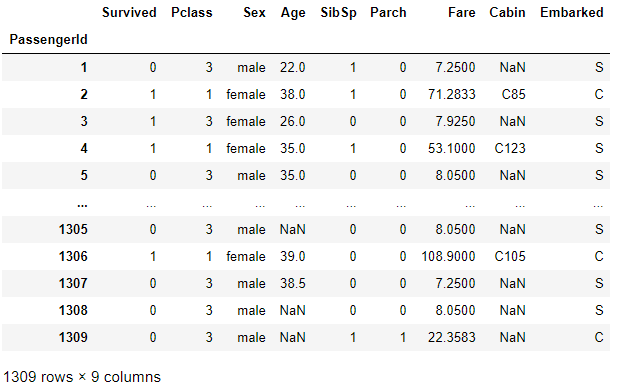

1.3. 칼럼 별 결측 값의 현황을 파악하자.

• 결측 값은 다른 행의 데이터들을 없애버릴 수 있으므로, 최우선 해결해야 할 과제다.
• 먼저, 각 칼럼 별 결측 값이 존재하는 칼럼과 그 개수를 파악하자.

# 컬럼별 결측값의 갯수 파악
>>> DF_Hand1.isnull().sum()

Survived       0
Pclass         0
Sex            0
Age          263
SibSp          0
Parch          0
Fare           1
Cabin       1014
Embarked       2
dtype: int64

• df.isnull(): DataFrame에서 결측 값(NaN)인 원소는 True로, 그렇지 않은 원소는 False로 나타낸다.
• df.sum(): DataFrame의 각 칼럼 별 합을 낸다.
• 위 결과를 보니, Cabin은 결측 값의 수가 지나치게 많아, 사용하지 않는 것이 좋다고 판단된다.
• Cabin은 객실 번호로, 객실 번호가 배에서 탈출하기 좋은 위치에 영향을 줄 수도 있다고 판단되나, 이미 이 정보를 담을 수 있는 다른 변수인 Pclass(티켓 등급), Fare(승객 요금), Embarked(기항지 위치)가 있으니, 제거해도 괜찮을 것으로 판단된다.
• Age는 총 데이터 1309개 중 263개에 해당하여, 차지하는 비중이 20%나 되지만, 생존에 큰 영향을 줄 수 있다고 판단되어, 보류하도록 하겠다.
• 결측 값은 Single Imputation으로 대체하지 않고, 일단 행 제거를 하여, 데이터의 양을 줄이는 쪽으로 방향을 잡도록 하겠다.
• 단순 대체로 평균을 넣는다거나, 의사 결정 나무, 회귀 모형을 통한 결측 값 추정이 가능하긴 하나, 일단은 이는 뒤로 미루자.

def missing_value(DF):

    # Cabin 변수를 제거하자
    del(DF["Cabin"])
    
    # 결측값이 있는 모든 행은 제거한다.
    DF.dropna(inplace = True)

• DataFrame.dropna(): 결측 값이 있는 행을 모두 제거한다.

# 결측값 처리
missing_value(DF_Hand1)
DF_Hand1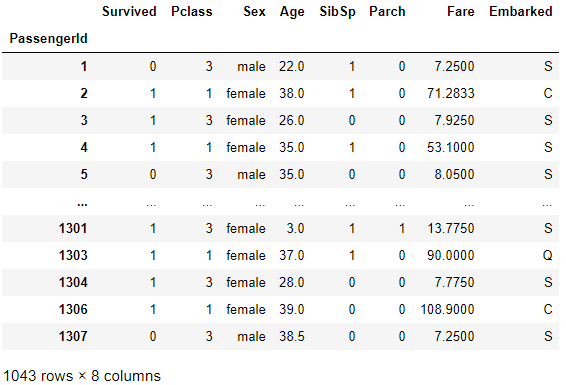

• 결측 값이 있는 행들을 제거하여, 총 행의 수가 1309개에서 1043개로 감소하였다.

1.4. 문자열 처리

• 머신러닝에 들어가는 Tensor에는 문자가 들어갈 수 없다.
• 모든 문자를 숫자로 바꾸도록 하자.
• 단순하게, 각 문자를 특정 숫자로 바꾸도록 하자.
• Sex: male = 0, female = 1
• Embarked: C = 0, Q = 1, S = 2

# 문자 데이터 처리
DF_Hand1["Sex"] = np.where(DF_Hand1["Sex"].to_numpy() == "male", 0, 1)
DF_Hand1["Embarked"] = np.where(DF_Hand1["Embarked"].to_numpy() == "C", 0,
                                np.where(DF_Hand1["Embarked"].to_numpy() == "Q", 1, 2))

>>> DF_Hand1

2. 데이터셋 분리 및 표준화

• 기본적인 데이터 전처리는 끝났으므로, 데이터셋을 Train과 Test, Label Dataset으로 분리하자.

2.1. 데이터셋 분리

• Train:Test = 7:3으로 분리해보자.
• Label Data도 분리하자.

# Label 생성
y_test, y_train = DF_Hand1["Survived"][:300].to_numpy(), DF_Hand1["Survived"][300:].to_numpy()

# Dataset 생성
del(DF_Hand1["Survived"])
X_test, X_train = DF_Hand1[:300].values, DF_Hand1[300:].values

• Series.to_numpy(), DataFrame.values 이 두 함수를 사용하면, 쉽게 array로 만들 수 있다.

>>> X_train
array([[  1.    ,   0.    ,  27.    , ...,   2.    , 211.5   ,   0.    ],
       [  3.    ,   0.    ,  20.    , ...,   0.    ,   4.0125,   0.    ],
       [  3.    ,   0.    ,  19.    , ...,   0.    ,   7.775 ,   2.    ],
       ...,
       [  3.    ,   1.    ,  28.    , ...,   0.    ,   7.775 ,   2.    ],
       [  1.    ,   1.    ,  39.    , ...,   0.    , 108.9   ,   0.    ],
       [  3.    ,   0.    ,  38.5   , ...,   0.    ,   7.25  ,   2.    ]])
       
>>> y_test
array([0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0,
       1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1,
       0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0,
       1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0,
       0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0,
       1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1,
       1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0,
       1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0,
       1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0,
       1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0,
       1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1,
       1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1], dtype=int64)

2.2. 표준화시켜주자.

• 숫자가 큰  Age,  Fare를 Train Dataset에 맞춰 최소-최대 스케일 변환해주자.

# 표준화
age_min = np.min(X_test[:,2])
age_max = np.max(X_test[:,2])

Fare_min = np.min(X_test[:,5])
Fare_max = np.max(X_test[:,5])

X_train[:,2] = (X_train[:,2] - age_min)/(age_max - age_min)
X_test[:,2] = (X_test[:,2] - age_min)/(age_max - age_min)

X_train[:,5] = (X_train[:,5] - Fare_min)/(Fare_max - Fare_min)
X_test[:,5] = (X_test[:,5] - Fare_min)/(Fare_max - Fare_min)

>>> X_train
array([[1.        , 0.        , 0.3729514 , ..., 2.        , 0.41282051,
        0.        ],
       [3.        , 0.        , 0.27319367, ..., 0.        , 0.00783188,
        0.        ],
       [3.        , 0.        , 0.25894257, ..., 0.        , 0.01517579,
        2.        ],
       ...,
       [3.        , 1.        , 0.38720251, ..., 0.        , 0.01517579,
        2.        ],
       [1.        , 1.        , 0.54396466, ..., 0.        , 0.21255864,
        0.        ],
       [3.        , 0.        , 0.53683911, ..., 0.        , 0.01415106,
        2.        ]])
        
>>> X_test
array([[3.        , 0.        , 0.30169588, ..., 0.        , 0.01415106,
        2.        ],
       [1.        , 1.        , 0.52971355, ..., 0.        , 0.13913574,
        0.        ],
       [3.        , 1.        , 0.3587003 , ..., 0.        , 0.01546857,
        2.        ],
       ...,
       [1.        , 0.        , 0.30169588, ..., 0.        , 0.26473857,
        0.        ],
       [3.        , 1.        , 0.0309249 , ..., 1.        , 0.04113566,
        2.        ],
       [3.        , 1.        , 0.30169588, ..., 0.        , 0.01415106,
        2.        ]])

• 이제 학습 준비가 어느 정도 완료되었다.

3. 모델 생성 및 학습하기

• 생존자 분류는 생존 or 사망으로 이진 분류이다.
• 이진 분류는 맨 마지막 출력층에서 Sigmoid 함수를 활성화 함수로 사용한다(참고: Sigmoid 함수).
• 손실 함수로는 binary cross Entropy를 사용한다(참고: binary crossentropy 함수).
• 분류이므로 compile에 metrics를 넣어 기준을 정해준다.

# 모델 생성
model = keras.Sequential()
model.add(Dense(128, activation = "relu"))
model.add(Dense(64, activation = "relu"))
model.add(Dense(32, activation = "relu"))
model.add(Dense(16, activation = "relu"))
model.add(Dense(1, activation = "sigmoid"))

# 모델 Compile
opt = keras.optimizers.Adam(learning_rate=0.005)
model.compile(optimizer=opt,
              loss = "binary_crossentropy",
              metrics=["binary_accuracy"])

>>> model.fit(X_train, y_train, epochs = 500)
Epoch 1/500
24/24 [==============================] - 1s 2ms/step - loss: 0.6112 - binary_accuracy: 0.6089
Epoch 2/500
24/24 [==============================] - 0s 2ms/step - loss: 0.3803 - binary_accuracy: 0.8494
Epoch 3/500
24/24 [==============================] - 0s 1ms/step - loss: 0.3446 - binary_accuracy: 0.8722
Epoch 4/500
24/24 [==============================] - 0s 1ms/step - loss: 0.3261 - binary_accuracy: 0.8778
Epoch 5/500
24/24 [==============================] - 0s 1ms/step - loss: 0.3600 - binary_accuracy: 0.8678

...

Epoch 496/500
24/24 [==============================] - 0s 1ms/step - loss: 0.1601 - binary_accuracy: 0.9350
Epoch 497/500
24/24 [==============================] - 0s 954us/step - loss: 0.1759 - binary_accuracy: 0.9169
Epoch 498/500
24/24 [==============================] - 0s 1ms/step - loss: 0.1753 - binary_accuracy: 0.9257
Epoch 499/500
24/24 [==============================] - 0s 997us/step - loss: 0.1667 - binary_accuracy: 0.9264
Epoch 500/500
24/24 [==============================] - 0s 1ms/step - loss: 0.1576 - binary_accuracy: 0.9289
<tensorflow.python.keras.callbacks.History at 0x15afa302b20>

• epochs를 500으로 주었으나, 손실 값이 0.1576으로 만족할 만큼 떨어지진 않은 것을 볼 수 있다.
• 그러나 이 손실 값은 상대적인 값이므로, 단순하게 접근해선 안된다.

4. 모델 평가하기

• 분류이므로, 모델을 평가하는 기준인 정확도는 실제 분류와 예측한 분류가 얼마나 일치하는지를 보면 될 것이다.

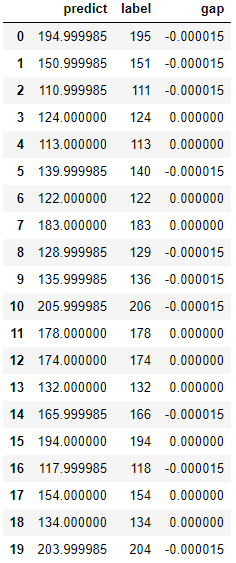
>>> pred = model.predict(X_test).reshape(X_test.shape[0])
>>> pred = np.where(pred > 0.5, 1, 0)
>>> accuracy = 1 - (np.where((pred - y_test) == 0, 0, 1).sum()/len(y_test))
>>> print("Accuracy:", accuracy)

Accuracy: 0.78

• 정확도가 0.78로 78%의 예측값만 실제와 일치하는 것으로 나타났다.
• 모델이 78%만 맞췄다는 것은, 모델의 분류 성능이 기대할만한 수준이라 보기가 힘들다고 할 수 있다.
• 그러나, 우리는 캐글의 Leaderboard를 보면 Titanic Dataset의 생존 분류의 예측률이 1.000으로 100%에 가까운 성능이 나온 것을 볼 수 있다!

• 대체 무슨 차이가 있길래 이 사람들이 만든 모델과 이번에 만든 모델의 성능 차이가 이토록 많이 날까?

 머신러닝은 보시다시피 마법의 상자가 아니라, 사용자가 얼마나 잘 설계를 하냐에 따라 전혀 다른 결과가 나오게 된다. 다음 포스트부턴 타이타닉 생존자 분류 모델의 성능을 올릴 수 있는 방법에 대해 학습해보도록 하겠다.

 이전 포스트에서 캐글에서 타이타닉 데이터를 다운로드하였다. 이번 포스트에서는 타이타닉 데이터를 파이썬으로 불러오고, 데이터가 어떻게 생겼고, 어떤 변수가 있는지를 확인해보자.

타이타닉 데이터 가져오기

• 이전에 받았던 타이타닉 데이터가 어떻게 생겼는지 보고, 변수들을 파악해보자.

1. 작업 파일 이동시키기

• 만약, 작성자와 같은 주피터 노트북 사용자라면, 아래와 같이 작업 파일과 같은 경로 안에 Data를 넣는 폴더를 만들어, 데이터를 넣어놓자.

• 현재 작업 중인 주피터 노트북 파일인 Report04_210209.ipynb와 같은 경로에 Dataset이라는 파일을 새로 만들었다.

• 이전에 다운로드하였던 titanic 압축파일 안에 있던 3 파일 "gender_submission.csv", "test.csv", "train.csv"을 Upload 시키자.

2. 데이터 불러오기

import pandas as pd
import numpy as np
import os

# Global Variable
file_path = "./Dataset"

# Function
def import_Data(file_path):

    result = dict()
    for file in os.listdir(file_path):

        file_name = file[:-4]
        result[file_name] = pd.read_csv(file_path + "/" + file)

    return result

Rawdata_dict = import_Data(file_path)

• os.listdir(디렉터리): 있는 파일 list를 가지고 온다.
• pd.read_csv(파일 경로): 있는 csv파일을 가지고 온다.
• 데이터를 이름으로 하나하나 불러오지 않고, 특정 디렉터리 안에 있는 모든 파일들을 해당 파일의 이름으로 딕셔너리에 넣어 가지고 왔다.
• 이렇게 데이터 프레임을 딕셔너리로 관리하는 경우, 특정 목적에 맞는 데이터들을 보다 쉽게 관리할 수 있으며, 데이터의 이름을 특정 패턴을 가진 상태로 부여할 수 있다.
• 또한, 한 번에 특정 디렉터리 내 모든 파일들을 모두 가져올 수 있으므로, 데이터를 가지고 올 때도 꽤 편하다.

3. 데이터가 어떻게 생겼는지 보도록 하자.

>>> dict_key = list(Rawdata_dict.keys())
>>> dict_key
['gender_submission', 'test', 'train']

>>> Rawdata_dict[dict_key[0]]

• gender_submission은 Row(행) 418개, Column(열, 변수) 2개로 구성된 데이터다.
• PassengerID: 승객 ID이다.
• Survived: 생존 여부로, 0 = 사망, 1 = 생존이다.

test.csv에 담긴 데이터를 보자

>>> Rawdata_dict[dict_key[1]]

• test는 Row(행) 418개, Column(열, 변수) 11개로 구성된 데이터다.
• PassengerID: 고객 번호
• Pclass: 티켓의 등급이다. 1 =1st(Upper), 2 = 2nd(Middle), 3 = 3rd(Lower)이다.
• Name: 승객의 이름
• Sex: 성별
• Age: 연령
• SibSp: 타이타닉호에 탑승한 형제/배우자의 수
• Parch: 타이타닉호에 탑승한 부모/자녀의 수
• Ticket: 티켓 번호
• Fare: 승객 요금
• Cabin: 객실 번호
• Embarked: 기항지 위치, C(Cherbourg), Q(Queenstown), S(Southampton)으로 3곳이 있다.

train.csv에 담긴 데이터를 보자

>>> Rawdata_dict[dict_key[2]]

• train은 Row(행) 891개, Column(열, 변수) 12개로 구성된 데이터다.
• 변수의 구성은 test와 동일하나, test와 달리 Survived라는 변수가 있다.
• test와 gender_submission은 PassengerID도 동일하며 Row의 수도 418개로 동일하다.
• 즉, test Dataset의 Survived는 gender_submission에 있는 것임을 알 수 있다.

 지금까지 타이타닉 데이터를 불러와서 구성하고 있는 데이터에 대해 차근차근 살펴보았다. 다음 포스트에서는 본격적으로 데이터 핸들링을 하여, 생존자 예측 모델을 만들어보도록 하겠다.

캐글(Kaggle)이란?

 빅데이터 분석에 관심이 있는 사람이라면, 한 번쯤 캐글(Kaggle)에 대해 들어봤을 것이다.

 캐글은 2010년 설립된 예측모델 및 분석대회 플랫폼으로, 기업 및 단체에서 데이터와 해결과제를 등록하면, 데이터 과학자들이 이를 해결하는 모델을 개발하고 경쟁하는 곳이다. 2017년 3월 구글에 인수되었다(위키피디아)

• 캐글(Kaggle)은 말 그대로 빅데이터 분석가들의 사냥터라고 할 수 있는데, 빅데이터 분석가들의 사냥감인 데이터가 널려 있으며, 서로서로 그 데이터를 얼마나 잘 요리했는지를 비교할 수도 있다.

1. Competitions

• 캐글 입장 후, Compete를 보면, 수많은 상금이 걸린 도전 과제들이 있는 것을 볼 수 있다.
• 여기서 마음에 드는 과제를 선택하면 "Join Competition"이라는 버튼이 생기는 것을 볼 수 있는데, 이를 클릭해서, 해당 대회에 참여할 수 있다.

• 위 사진에서 각 버튼은 다음 기능을 한다.

1. Overview: 문제에 대한 소개와 정의
2. Data: 예측 모델 생성에 필요한 데이터셋과 Feature가 되는 Fields가 설명되어 있으며, 대회에 쓰일 데이터 셋을 다운로드할 수 있다.
3. Code: 대회 참가 시, 캐글에서 제공하는 서버에서 작업할 수 있게 해 주며, 다른 사람의 코드를 참고할 수 있음.
4. Discussion: 질의응답 공간
5. Leaderboard: 모델의 정확도를 기준으로 랭킹이 매겨지는 곳
6. Dadataset: 관련 데이터 셋을 볼 수 있다.

• 대회 진행 방식은 데이터를 다운로드하여 내 PC에서 작업하거나 캐글에서 제공하는 서버에 접속해 작업을 하는 방식이 있다.

• 대회 참가 후, Code를 클릭하면 New Notebook을 눌러, 커널에 접속할 수 있다.

• 여기서 코드를 작성할 수 있으며, 그 코드가 정상적으로 실행된다면, Commit 하여, 결과를 업로드하고 정확도를 기반으로 점수를 확인할 수 있다.
• 상위 랭킹에 들어간다면, 그에 대한 대회의 보상을 받을 수도 있다고 하니, 실력도 늘리고, 용돈 벌이도 할 겸 해서 한 번쯤 해보는 것을 추천한다.

2. 타이타닉 데이터

• 이번에 학습에 사용해볼 데이터인 타이타닉 데이터를 구해보자.
• 위 과정을 통해 직접 찾아갈 수도 있으나, 이 버튼을 눌러서 바로 이동할 수도 있다.

• 타이타닉 데이터의 변수별 정보는 다음과 같다.

• 이곳에서 Titanic Data를 다운로드할 수 있으며, 데이터의 칼럼 별 개형 등을 볼 수도 있다.
• 데이터의 각 변수에 대한 정보를 최대한 얻은 다음 분석을 시작하도록 하자.

 이밖에도 캐글은 커뮤니티나 빅데이터 분석의 기반이 되는 것들을 공부할 수 있는(Courses) 공간도 따로 제공하므로, 많이 사용해보도록 하자.

 다음 포스트에서는 이번에 받은 타이타닉 데이터를 이용해서, 생존자 예측 모델을 만들어보도록 하겠다.

 이전에 학습했던 모델은 Input 되는 Node의 수가 2개인 모델이었다. Input Node의 수를 3개 이상으로 하는 방법도 크게 다르지 않다. 이번 포스트에서는 Output Node의 수를 2개로 해보도록 하겠다.

학습 목표

• 연속형 데이터를 이용하여 Input Node가 3개이고, Output Node가 2개인 데이터를 컴퓨터가 맞추도록 해보자.
• 패턴:

$$h(x)=\begin{cases}y_1=0.3x_1+0.2x_2-0.4x_3+0.1x_4+2 \\  y_2=0.5x_1-0.1x_2+0.3x_3+0x_4-2\end{cases}$$

구현해보자.

1. 데이터셋 생성

# import mudule
import pandas as pd
import numpy as np
from tensorflow import keras
from tensorflow.keras.layers import Dense

# Dataset 생성
def f1(x1, x2, x3, x4):
    return 0.3*x1 + 0.2*x2 - 0.4*x3 + 0.1*x4 + 2


def f2(x1, x2, x3, x4):
    return 0.5*x1 - 0.1*x2 + 0.3*x3 - 2


def make_dataset(start_N, end_N):
    
    x1 = np.arange(start_N, end_N)
    x2 = x1 + 1
    x3 = x1 + 2
    x4 = x1 + 3
    
    y1 = f1(x1, x2, x3, x4)
    y2 = f2(x1, x2, x3, x4)
    
    append_for_shuffle = np.c_[x1, x2, x3, x4, y1, y2]
    np.random.shuffle(append_for_shuffle)
    
    X = append_for_shuffle[:,[0,1,2,3]]
    y = append_for_shuffle[:,[4,5]]
    
    return X, y

X, y = make_dataset(0, 1000)
X_train, X_test = X[:800], X[800:]
y_train, y_test = y[:800], y[800:]

• 생성된 Dataset을 보자.

>>> X_train
array([[491., 492., 493., 494.],
       [ 47.,  48.,  49.,  50.],
       [755., 756., 757., 758.],
       ...,
       [445., 446., 447., 448.],
       [429., 430., 431., 432.],
       [881., 882., 883., 884.]])
       
>>> y_train
array([[ 99.9, 342.2],
       [ 11.1,  31.4],
       [152.7, 527. ],
       ...,
       [ 90.7, 310. ],
       [ 87.5, 298.8],
       [177.9, 615.2]])

2. 모델 생성 및 학습

# 모델 생성 및 Compile 실시
model = keras.Sequential()
model.add(Dense(128, activation = "relu"))
model.add(Dense(64, activation = "relu"))
model.add(Dense(32, activation = "relu"))
model.add(Dense(16, activation = "relu"))
model.add(Dense(2, activation = "linear"))

opt = keras.optimizers.Adam(learning_rate=0.005)
model.compile(optimizer = opt, loss = "mse")

# 표준화
min_key = np.min(X_train)
max_key = np.max(X_train)

X_std_train = (X_train - min_key)/(max_key - min_key)
y_std_train = (y_train - min_key)/(max_key - min_key)
X_std_test = (X_test - min_key)/(max_key - min_key)

>>> model.fit(X_std_train, y_std_train, epochs = 100)

Epoch 1/100
25/25 [==============================] - 1s 1ms/step - loss: 0.0181
Epoch 2/100
25/25 [==============================] - 0s 1ms/step - loss: 1.9474e-04
Epoch 3/100
25/25 [==============================] - 0s 1ms/step - loss: 2.2225e-05
Epoch 4/100
25/25 [==============================] - 0s 1ms/step - loss: 3.8012e-06
Epoch 5/100
25/25 [==============================] - 0s 1ms/step - loss: 7.8100e-07
Epoch 6/100
25/25 [==============================] - 0s 1ms/step - loss: 3.6994e-07

...

Epoch 96/100
25/25 [==============================] - 0s 1ms/step - loss: 1.1601e-07
Epoch 97/100
25/25 [==============================] - 0s 1ms/step - loss: 1.8677e-07
Epoch 98/100
25/25 [==============================] - 0s 956us/step - loss: 3.6037e-07
Epoch 99/100
25/25 [==============================] - 0s 878us/step - loss: 3.3609e-07
Epoch 100/100
25/25 [==============================] - 0s 873us/step - loss: 1.9744e-07
<tensorflow.python.keras.callbacks.History at 0x1d068dd0670>

>>> def MAE(x, y):
>>>     return np.mean(np.abs(x - y))

>>> pred = model.predict(X_std_test) * (max_key - min_key) + min_key
>>> print("Accuracy:", MAE(pred, y_test))
Accuracy: 0.1379637644290885

• 정확도(Accuracy)는 0.137로 만족스러울 정도는 아니지만 그리 나쁘진 않게 나왔다.
• 정확도는 평균 절댓값 오차(MAE)로 구하였으므로, RMSE보다 실제 편차에 더 가깝다고 할 수 있다.
• 실제 데이터의 생김새를 보자.

DF = pd.DataFrame(pred, columns=["y1_pred", "y2_pred"])
DF[["y1_label", "y2_label"]] = y_test
DF["y1_gap"] = DF["y1_label"]-DF["y1_pred"]
DF["y2_gap"] = DF["y2_label"]-DF["y2_pred"]
DF[["y1_pred", "y1_label", "y1_gap", "y2_pred", "y2_label", "y2_gap"]]

• 만족스러운 수준은 아니지만, 실제 데이터와 예측 데이터가 꽤 유사하게 나왔다.

 지금까지 가볍게 연속형 데이터를 이용해서 숨겨진 패턴을 찾아보았다. 다음 포스트에서는 머신러닝을 할 때, 가장 처음 사용하게 되는 실제 데이터인 타이타닉 데이터를 이용해서 생존 여부를 분류해보도록 하겠다.

 이전 포스트에서 변수가 1개인 Input이 들어가 Output이 1개인 모델을 만들어보았다. 이번 포스트에서는 Input이 2개고, Output이 1개인 모델을 만들어보도록 하겠다.

학습 목표

• 이전 패턴보다 컴퓨터가 인지하기 어려운 패턴을 컴퓨터가 찾아내도록 해보자.
• 패턴: $ f(x)=\frac{1}{2}x_1^2-3x_2+5 $

1. 이전 방식대로 모델을 만들고 평가해보자.

• 이전 모델을 생성했던 방법대로 데이터셋을 생성하고 학습을 시켜서 패턴을 찾는지 확인해보자.

# Import Module
import pandas as pd
import numpy as np
from tensorflow import keras
from tensorflow.keras.layers import Dense

# Dataset 만들기
np.random.seed(1234)

def f2(x1, x2):
    
    return 0.5*x1**2 - 3*x2 + 5

X0_1 = np.random.randint(0, 100, (1000))
X0_2 = np.random.randint(0, 100, (1000))
X_train = np.c_[X0_1, X0_2]
y_train = f2(X0_1, X0_2)

X1_1 = np.random.randint(100, 200, (300))
X1_2 = np.random.randint(100, 200, (300))
X_test = np.c_[X1_1, X1_2]
y_test = f2(X1_1, X1_2)

# make model
model = keras.Sequential()
model.add(Dense(16, activation = 'relu'))
model.add(Dense(32, activation = 'relu'))
model.add(Dense(16, activation = 'relu'))
model.add(Dense(1, activation = 'linear'))


# Compile
opt = keras.optimizers.Adam(learning_rate=0.005)
model.compile(optimizer=opt, loss='mse')


# Standardization
mean_key = np.mean(X_train)
std_key = np.std(X_train)

X_train_std = (X_train - mean_key)/std_key
y_train_std = (y_train - mean_key)/std_key

X_test_std = (X_test - mean_key)/std_key

>>> model.fit(X_train_std, y_train_std, epochs = 100)

Epoch 1/100
32/32 [==============================] - 1s 972us/step - loss: 4486.5587
Epoch 2/100
32/32 [==============================] - 0s 1ms/step - loss: 2577.3394
Epoch 3/100
32/32 [==============================] - 0s 974us/step - loss: 135.0658
Epoch 4/100
32/32 [==============================] - 0s 1ms/step - loss: 39.6805
Epoch 5/100
32/32 [==============================] - 0s 1ms/step - loss: 26.0182
Epoch 6/100
32/32 [==============================] - 0s 1ms/step - loss: 23.2357

...

Epoch 96/100
32/32 [==============================] - ETA: 0s - loss: 0.870 - 0s 730us/step - loss: 0.9306
Epoch 97/100
32/32 [==============================] - 0s 835us/step - loss: 0.4291
Epoch 98/100
32/32 [==============================] - 0s 792us/step - loss: 0.5671
Epoch 99/100
32/32 [==============================] - 0s 856us/step - loss: 0.3809
Epoch 100/100
32/32 [==============================] - 0s 708us/step - loss: 0.4041
<tensorflow.python.keras.callbacks.History at 0x21cdb6c0b80>

>>> pred = (model.predict(X_test_std) * std_key) + mean_key
>>> pred = pred.reshape(pred.shape[0])
>>> print("Accuracy:", np.sqrt(np.sum((y_test - pred)**2))/len(y_test))
Accuracy: 209.2436541220142

• 이전 포스트처럼 시험 데이터 셋과 학습 데이터 셋을 전혀 겹치지 않는 영역으로 만들어보았다.
• 손실 값은 0에 가깝게 줄어들었으나, 정확도(Accuracy)가 209.243으로 매우 낮은 것을 알 수 있다.
• 예측값과 라벨의 차이가 어느 정도인지 확인해보자.

result_DF = pd.DataFrame({"predict":pred, "label":y_test})
result_DF["gap"] = result_DF["label"] - result_DF["predict"]
result_DF

• 위 데이터를 보면, 실제(label)와 예측값(predict)의 차이가 매우 크게 나는 것을 볼 수 있다.
• 대체 왜 이런 현상이 발생한 것일까?

2. 학습에 맞는 데이터셋 만들기

• 이전 학습에서 숨겨져 있던 패턴은 다음과 같다.
• $h(x) = x + 10 $
• 위 패턴은 아주 단순한 선형 함수이므로, 학습 데이터 셋과 거리가 있는 데이터라 할지라도, 쉽게 예측할 수 있다.
• 그러나, 이번에 숨겨진 패턴인 $f(x)=\frac{1}{2}x_1^2-3x_2+5$은 $x^2$의 존재로 인해 선형 함수가 아니며, 해가 2개이므로, 이전에 비해 꽤 복잡해졌다.
• 이번엔 train Dataset에서 test Dataset을 분리해서 학습해보자.
• 단, train Dataset과 test Dataset은 절대 중복되선 안 된다.

# Dataset 만들기
np.random.seed(1234)

def f2(x1, x2):
    
    return 0.5*x1**2 - 3*x2 + 5

X1 = np.random.randint(0, 100, (1000))
X2 = np.random.randint(0, 100, (1000))
X = np.c_[X1, X2]
y = f2(X1, X2)

# 데이터셋을 중복되지 않게 만든다.
Xy = np.c_[X, y]
Xy = np.unique(Xy, axis = 0)
np.random.shuffle(Xy)
test_len = int(np.ceil(len(Xy)*0.3))
X = Xy[:, [0,1]]
y = Xy[:, 2]

# test Dataset과 train Dataset으로 나누기
X_test = X[:test_len]
y_test = y[:test_len]

X_train = X[test_len:]
y_train = y[test_len:]

• np.c_[array1, array2]: 두 array를 열 기준으로 붙인다.
• np.unique(array, axis = 0): array에서 unique 한 값만 추출한다(axis를 어떻게 잡느냐에 따라 다른 결과를 가지고 올 수 있다).
• np.random.shuffle(array): array를 랜덤 하게 섞는다
• np.ceil(float): float을 올림 한다.
• 데이터셋을 중복되지 않게 만들어, test set과 train set이 중복되어 Accuracy가 낮게 나오는 현상을 피한다.

# make model
model = keras.Sequential()
model.add(Dense(16, activation = 'relu'))
model.add(Dense(32, activation = 'relu'))
model.add(Dense(16, activation = 'relu'))
model.add(Dense(1, activation = 'linear'))


# Compile
opt = keras.optimizers.Adam(learning_rate=0.005)
model.compile(optimizer=opt, loss='mse')


# Standardization
mean_key = np.mean(X_train)
std_key = np.std(X_train)

X_train_std = (X_train - mean_key)/std_key
y_train_std = (y_train - mean_key)/std_key

X_test_std = (X_test - mean_key)/std_key

# Model Learning
>>> model.fit(X_train_std, y_train_std, epochs = 100)

Epoch 1/100
139/139 [==============================] - 1s 912us/step - loss: 2999.6784
Epoch 2/100
139/139 [==============================] - 0s 943us/step - loss: 26.4051
Epoch 3/100
139/139 [==============================] - 0s 1ms/step - loss: 14.5395
Epoch 4/100
139/139 [==============================] - 0s 1ms/step - loss: 9.9778
Epoch 5/100
139/139 [==============================] - 0s 814us/step - loss: 7.2809
Epoch 6/100
139/139 [==============================] - 0s 777us/step - loss: 5.1137
Epoch 7/100

...

Epoch 96/100
139/139 [==============================] - 0s 1ms/step - loss: 0.0378
Epoch 97/100
139/139 [==============================] - 0s 931us/step - loss: 0.0468
Epoch 98/100
139/139 [==============================] - 0s 821us/step - loss: 0.0808
Epoch 99/100
139/139 [==============================] - 0s 745us/step - loss: 0.1535
Epoch 100/100
139/139 [==============================] - 0s 793us/step - loss: 0.0493
<tensorflow.python.keras.callbacks.History at 0x260b7b33c70>

>>> pred = (model.predict(X_test_std) * std_key) + mean_key
>>> pred = pred.reshape(pred.shape[0])
>>> print("Accuracy:", np.sqrt(np.sum((y_test - pred)**2))/len(y_test))
Accuracy: 0.9916198414587479

• 데이터 셋만 바꿨는데, 이전 데이터 셋의 정확도(Accuracy)가 209.243에서 0.9916으로 큰 폭으로 떨어진 것을 볼 수 있다.
• 실제 예측 결과가 어떻게 생겼는지 확인해보자.

result_DF = pd.DataFrame({"predict":pred, "label":y_test})
result_DF["gap"] = result_DF["label"] - result_DF["predict"]
result_DF

• 차이가 있긴 하지만, 실제 데이터와 상당히 가까워졌다.
• 이번엔 데이터의 양을 늘려서 학습시켜보자.

3. 데이터의 양을 늘려보자.

# Import Module
import pandas as pd
import numpy as np
from tensorflow import keras
from tensorflow.keras.layers import Dense




# Dataset 만들기
np.random.seed(1234)

def f2(x1, x2):
    
    return 0.5*x1**2 - 3*x2 + 5

X1 = np.random.randint(0, 100, (30000))
X2 = np.random.randint(0, 100, (30000))
X = np.c_[X1, X2]
y = f2(X1, X2)

# 데이터셋을 중복되지 않게 만든다.
Xy = np.c_[X, y]
Xy = np.unique(Xy, axis = 0)
np.random.shuffle(Xy)
test_len = int(np.ceil(len(Xy)*0.2))
X = Xy[:, [0,1]]
y = Xy[:, 2]

# test Dataset과 train Dataset으로 나누기
X_test = X[:test_len]
y_test = y[:test_len]

X_train = X[test_len:]
y_train = y[test_len:]




# make model
model = keras.Sequential()
model.add(Dense(32, activation = 'elu'))
model.add(Dense(32, activation = 'elu'))
model.add(Dense(1, activation = 'linear'))


# Compile
opt = keras.optimizers.Adam(learning_rate=0.005)
model.compile(optimizer=opt, loss='mse')


# min-max scaling
min_key = np.min(X_train)
max_key = np.max(X_train)

X_train_std = (X_train - min_key)/(max_key - min_key)
y_train_std = (y_train - min_key)/(max_key - min_key)

X_test_std = (X_test - min_key)/(max_key - min_key)

>>> model.fit(X_train_std, y_train_std, epochs = 100)

Epoch 1/100
238/238 [==============================] - 1s 970us/step - loss: 168.8257
Epoch 2/100
238/238 [==============================] - 0s 1ms/step - loss: 4.6773A: 0s - loss: 5.8
Epoch 3/100
238/238 [==============================] - 0s 821us/step - loss: 1.2054
Epoch 4/100
238/238 [==============================] - 0s 842us/step - loss: 0.4222
Epoch 5/100
238/238 [==============================] - 0s 781us/step - loss: 0.1056
Epoch 6/100
238/238 [==============================] - 0s 851us/step - loss: 0.0459

...

Epoch 96/100
238/238 [==============================] - 0s 736us/step - loss: 4.2894e-04
Epoch 97/100
238/238 [==============================] - 0s 741us/step - loss: 5.0023e-04
Epoch 98/100
238/238 [==============================] - 0s 720us/step - loss: 0.0046
Epoch 99/100
238/238 [==============================] - 0s 749us/step - loss: 0.0036
Epoch 100/100
238/238 [==============================] - 0s 812us/step - loss: 0.0189
<tensorflow.python.keras.callbacks.History at 0x24611ae5910>

>>> pred = (model.predict(X_test_std) * (max_key - min_key)) + min_key
>>> pred = pred.reshape(pred.shape[0])
>>> print("Accuracy:", np.sqrt(np.sum((y_test - pred)**2))/len(y_test))
Accuracy: 0.03539701825569002

result_DF = pd.DataFrame({"predict":pred, "label":y_test})
result_DF["gap"] = result_DF["label"] - result_DF["predict"]
result_DF

• 중복을 제거하여 데이터의 양을 953개에서 9,493개로 늘렸다.
• 그로 인해 Accuracy가 0.9916에서 0.0353으로 감소하여, 정확도가 보다 올라갔다.
• 이상치가 존재하지 않는 데이터이므로, 최소-최대 스케일 변환(min-max scaling)을 이용해 표준화를 시켰다. 그로 인해, Accuracy가 크게 변하지는 않았으나, 이전에 비해 손실 값이 빠르게 0에 수렴하는 것을 볼 수 있다.
• 활성화 함수를 relu가 아닌 elu를 사용하였다. 성능 차이가 그리 크지는 않으나, 손실 값과 Accuracy에 긍정적인 영향을 미쳤다.
• 네트워크의 노드 수와 Layer의 수를 바꿨다.

 지금까지 변수가 2개인 데이터 셋을 학습시키는 과정을 해보았다. 숨어있는 패턴이 복잡하고 변수의 수가 늘어났더니, 처음 보는 영역에 있는 데이터를 제대로 분류하지 못하는 현상이 발생하였다.

 이 때는 학습 데이터셋에 시험 데이터셋과 유사한 데이터 셋을 포함시키는 것이 가장 좋은 해결 방법이다. 위처럼 시험 데이터 셋과 학습 데이터 셋이 중복되지 않는다 할지라도, 유사한 영역에 있는 경우 제대로 예측하는 것을 볼 수 있다.

 이전 포스트에서 데이터 셋을 표준 정규분포로 만들어 더 쉽게 데이터셋을 모델에 학습시켜보았다. 그러나, 패턴의 단순함에 비해 여전히 정확도(Accuracy)가 원하는 수준까지 나오질 않는다. 대체 왜 그럴까?

 이번 포스트에서는 경험적 하이퍼 파라미터 튜닝 방법을 사용하여, 하이퍼 파라미터를 튜닝해보도록 하겠다. 제대로 된 하이퍼 파라미터 튜닝은 추후 자세히 다루도록 하겠다.

하이퍼 파라미터 튜닝(HyperParameter Tuning)

• 머신러닝을 공부하다 보면 하이퍼 파라미터라는 단어와 파라미터라는 단어가 반복해서 등장하는 것을 볼 수 있다. 
• 파라미터(Parmeter)라는 단어는 코딩을 하다 보면 자주 보이는, 수정할 수 있는 값인데, 갑자기 왜 하이퍼 파라미터라는 값이 등장할까? 또, 왜 파라미터는 수정할 수 없는 값이라고 할까?
• 머신러닝에서의 파라미터는 가중치(Weight), 편향(Bias) 같은 학습 과정에서 모델이 자동으로 업그레이드하며 갱신하는 값을 가리킨다.
• 파라미터는 학습 도중 머신이 알아서 바꿔가는 것이므로, 연구자가 손 델 수 있는 값이 아니다.
• 머신러닝에서 하이퍼 파라미터는 그 외 연구자가 수정할 수 있는 값으로, 학습률, Optimizer, 활성화 함수, 손실 함수 등 다양한 인자들을 가리킨다.
• 이 값들을 손보는 이유는 모델이 학습에 사용한 데이터 셋의 형태를 정확히 알지 못하고, 데이터 셋의 형태에 따라 이들을 사용하는 방법이 바뀌기 때문이다.

1. 하이퍼 파라미터 튜닝을 해보자.

• 우리는 이미 우리가 만들어낸 데이터 셋의 형태를 알고 있다.
• 우리가 만들어낸 데이터셋은 선형 데이터셋인데, 우리는 활성화 함수로 은닉층에서 ReLU를 사용하였다.
• 이번엔 모든 활성화 함수를 linear로 만들어 학습시켜보자.

# Import Module
import pandas as pd
import numpy as np
from tensorflow import keras
from tensorflow.keras.layers import Dense



# Dataset Setting
def f(x):
    return x + 10
    
# Data set 생성
np.random.seed(1234)   # 동일한 난수가 나오도록 Seed를 고정한다.
X_train = np.random.randint(0, 100, (100, 1))
X_test = np.random.randint(100, 200, (20, 1))

# Label 생성
y_train = f(X_train)
y_test = f(X_test)


# Model Setting
model = keras.Sequential()
model.add(Dense(16, activation='linear'))
model.add(Dense(1, activation='linear'))


# Compile: 학습 셋팅
opt = keras.optimizers.Adam(learning_rate=0.01)
model.compile(optimizer=opt, loss = 'mse')


# 특성 스케일 조정
mean_key = np.mean(X_train)
std_key = np.std(X_train)

X_train_std = (X_train - mean_key)/std_key
y_train_std = (y_train - mean_key)/std_key
X_test_std = (X_test - mean_key)/std_key

# 학습
>>> model.fit(X_train_std, y_train_std, epochs = 100)

Epoch 1/100
4/4 [==============================] - 0s 2ms/step - loss: 2.5920
Epoch 2/100
4/4 [==============================] - 0s 997us/step - loss: 1.5766
Epoch 3/100
4/4 [==============================] - 0s 2ms/step - loss: 0.7499
Epoch 4/100
4/4 [==============================] - 0s 2ms/step - loss: 0.3371
Epoch 5/100
4/4 [==============================] - 0s 2ms/step - loss: 0.0817
Epoch 6/100
4/4 [==============================] - 0s 2ms/step - loss: 0.0059

...

Epoch 95/100
4/4 [==============================] - 0s 1ms/step - loss: 6.0676e-15
Epoch 96/100
4/4 [==============================] - 0s 1ms/step - loss: 6.2039e-15
Epoch 97/100
4/4 [==============================] - 0s 2ms/step - loss: 6.4773e-15
Epoch 98/100
4/4 [==============================] - 0s 2ms/step - loss: 5.6185e-15
Epoch 99/100
4/4 [==============================] - 0s 1ms/step - loss: 6.5939e-15
Epoch 100/100
4/4 [==============================] - 0s 1ms/step - loss: 6.7939e-15
<tensorflow.python.keras.callbacks.History at 0x26e75c29e80>

# label과 test set을 비교해보자.
pred = model.predict(X_test_std.reshape(X_test_std.shape[0]))
pred_restore = pred * std_key + mean_key
predict_DF = pd.DataFrame({"predict":pred_restore.reshape(pred_restore.shape[0]), "label":y_test.reshape(y_test.shape[0])})
predict_DF["gap"] = predict_DF["predict"] - predict_DF["label"]
predict_DF

# 정확도(Accuracy)를 보자
>>> print("Accuracy:", np.sqrt(np.mean((pred_restore - y_test)**2)))
Accuracy: 1.0789593218788873e-05

• 고작, 은닉층의 활성화 함수만 바꿨을 뿐인데, 이전보다 훨씬 좋은 결과가 나왔다.
• 패턴을 거의 완벽하게 찾아내었으며, 정확도(Accuracy) 역시 0.000010789(e-05는 $10^{-5}$을 하라는 소리다.)로 거의 0에 근사하게 나왔다.

2. 정리

• 위 결과를 보면, 아무리 단순한 패턴이라 할지라도, 그 데이터 셋의 형태를 반영하지 못한다면, 정확히 그 결과를 찾아내지 못할 수 있다는 것을 알 수 있다.
• 인공지능은 흔히들 생각하는 빅데이터를 넣으면, 그 안에 숨어 있는 패턴이 자동으로 나오는 마법의 상자가 아니라, 연구자가 그 데이터에 대한 이해를 가지고 여러 시도를 해, 제대로 된 설계를 해야만 내가 원하는 제대로 된 패턴을 찾아낼 수 있는 도구다.
• 그러나, 실전에서는 지금처럼 우리가 이미 패턴을 알고 있는 경우는 없기 때문에 다양한 도구를 이용해서, 데이터를 파악하고, 적절한 하이퍼 파라미터를 찾아낸다.
• 넣을 수 있는 모든 하이퍼 파라미터를 다 넣어보는 "그리드 서치(Greed search)"나 랜덤 한 값을 넣어보고 지정한 횟수만큼 평가하는 "랜덤 서치(Random Search)", 순차적으로 값을 넣어보고, 더 좋은 해들의 조합에 대해서 찾아가는 "베이지안 옵티마이제이션(Bayesian Optimization)" 등 다양한 방법이 있다.
• 같은 알고리즘이라 할지라도, 데이터를 어떻게 전처리하느냐, 어떤 활성화 함수를 쓰느냐, 손실 함수를 무엇을 쓰느냐 등과 같은 다양한 요인으로 인해 다른 결과가 나올 수 있으므로, 경험을 많이 쌓아보자.

 이전 포스트에서 만든 모델의 결과는 그리 나쁘진 않았으나, 패턴이 아주 단순함에도 쉽게 결과를 찾아내지 못했고, 학습에 자원 낭비도 많이 되었다.

 왜 그럴까?

특성 스케일 조정

• 특성 스케일 조정을 보다 쉽게 말해보면, 표준화라고 할 수 있다.
• 이번에 학습한 대상은 변수(다른 정보에 대한 벡터 성분)가 1개밖에 없어서 그나마 나았으나, 만약, 키와 몸무게가 변수로 주어져 벡터의 원소로 들어갔다고 생각해보자.
• 키나 몸무게는 그 자리 수가 너무 큰 값이다 보니, 파라미터 역시 그 값의 변화가 지나치게 커지게 되고, 그로 인해 제대로 된 결과를 찾지 못할 수 있다.
• 또한 키와 몸무게는 그 단위마저도 크게 다르다 보니, 키에서 160이 몸무게에서의 160과 같다고 볼 수 있다. 그러나 모두가 알다시피 키 160은 대한민국 남녀 성인 키 평균에 못 미치는 값이며, 몸무게 160은 심각한 수준의 비만이다. 전혀 다른 값임에도 이를 같게 볼 위험이 있다는 것이다.
• 이러한 표준화가 미치는 영향은 손실 함수에서 보다 이해하기 쉽게 볼 수 있는데, 이로 인해 발생하는 문제가 바로 경사 하강법의 zigzag 문제다.

• $w_1$과 $w_2$의 스케일 크기가 동일하다면(값의 범위가 동일), 손실 함수가 보다 쉽게 최적해에서 수렴할 수 있다.

• $w_1$과 $w_2$의 스케일 크기가 많이 다르다면, 손실 함수는 쉽게 최적해에 수렴하지 못한다.

1. 특성 스케일 조정 방법

• 특성 스케일 조정 방법은 크게 2가지가 있다.
• 첫 번째는 특성 스케일 범위 조정이고, 두 번째는 표준 정규화를 하는 것이다.

A. 특성 스케일 범위 조정

• 특성 스케일 범위 조정은 말 그대로, 값의 범위를 조정하는 것이다.
• 바꿀 범위는 [0, 1]이다.
• 이 방법에는 최솟값과 최댓값이 사용되므로 "최소-최대 스케일 변환(min-max scaling)"이라고도 한다.
• 공식은 다음과 같다.

$$ x_{norm} = \frac{x_i-x_{min}}{x_{max}-x_{min}} $$

• 위 공식에서 $x_i$는 표준화를 할 대상 array다.
• 범위 축소에 흔히들 사용되는 해당 방법은, 가장 쉽게 표준화하는 방법이지만, 값이 지나치게 축소되어 존재하던 이상치가 사라져 버릴 수 있다.
• 특히나, 이상치가 존재한다면, 이상치보다 작은 값들을 지나치게 좁은 공간에 모아버리게 된다.

B. 표준 정규분포

• 표준 정규분포는 평균 = 0, 표준편차 = 1로 바꾸는 가장 대표적인 표준화 방법이다.
• 공식은 다음과 같다.

$$ x_{std} = \frac{x_i - \mu_x}{\sigma_x} $$

• 위 공식에서 $x_i$는 표준화 대상 array다.
• 표준 정규분포로 만들게 되면, 평균 = 0, 표준편차 = 1로 값이 축소되게 되지만, 여전히 이상치의 존재가 남아 있기 때문에 개인적으론 표준 정규분포로 만드는 것을 추천한다.

 특성 스케일 조정에서 가장 중요한 것은, 조정의 기준이 되는 최솟값, 최댓값, 평균, 표준편차는 Train Dataset의 값이라는 것이다. 해당 방법 사용 시, Train Dataset을 기준으로 하지 않는다면, Test Dataset의 값이 Train Dataset과 같아져 버릴 수 있다.

2. 표준 정규분포를 이용해서 특성 스케일을 조정해보자.

# Import Module
import pandas as pd
import numpy as np
from tensorflow import keras
from tensorflow.keras.layers import Dense



# Dataset Setting
def f(x):
    return x + 10
    
# Data set 생성
np.random.seed(1234)   # 동일한 난수가 나오도록 Seed를 고정한다.
X_train = np.random.randint(0, 100, (100, 1))
X_test = np.random.randint(100, 200, (20, 1))

# Label 생성
y_train = f(X_train)
y_test = f(X_test)


# Model Setting
model = keras.Sequential()
model.add(Dense(16, activation='relu'))
model.add(Dense(1, activation='linear'))


# Compile: 학습 셋팅
opt = keras.optimizers.Adam(learning_rate=0.01)
model.compile(optimizer=opt, loss = 'mse')

mean_key = np.mean(X_train)
std_key = np.std(X_train)

X_train_std = (X_train - mean_key)/std_key
y_train_std = (y_train - mean_key)/std_key
X_test_std = (X_test - mean_key)/std_key

• 앞의 모델 생성 및 Compile 단계까진 동일하나, 뒤에 표준화 과정이 추가된다.
• Train Dataset의 평균과 표준편차는 test의 Dataset이 나중에 주어져 현재 할 수 없거나, predict의 결과 원상 복귀에 사용되므로, 따로 Scalar 값을 빼놓자.

>>> model.fit(X_train_std, y_train_std, epochs = 100)

Epoch 1/100
4/4 [==============================] - 0s 1ms/step - loss: 0.5749
Epoch 2/100
4/4 [==============================] - 0s 1ms/step - loss: 0.2483
Epoch 3/100
4/4 [==============================] - 0s 3ms/step - loss: 0.0814
Epoch 4/100
4/4 [==============================] - 0s 2ms/step - loss: 0.0217
Epoch 5/100
4/4 [==============================] - 0s 2ms/step - loss: 0.0378
Epoch 6/100
4/4 [==============================] - 0s 1ms/step - loss: 0.0402

...

Epoch 95/100
4/4 [==============================] - 0s 2ms/step - loss: 4.5394e-06
Epoch 96/100
4/4 [==============================] - 0s 1ms/step - loss: 5.2252e-06
Epoch 97/100
4/4 [==============================] - 0s 2ms/step - loss: 5.7370e-06
Epoch 98/100
4/4 [==============================] - 0s 2ms/step - loss: 5.9242e-06
Epoch 99/100
4/4 [==============================] - 0s 2ms/step - loss: 5.8228e-06
Epoch 100/100
4/4 [==============================] - 0s 2ms/step - loss: 5.6276e-06
<tensorflow.python.keras.callbacks.History at 0x234ff82a520>

• 이전에 비해 적은 epochs(=100)로 빠르게 손실 값이 0에 수렴하는 것을 볼 수 있다.
• 결과를 보도록 하자.

pred = model.predict(X_test_std.reshape(X_test_std.shape[0]))

# 원상복구
pred_restore = pred * std_key + mean_key
predict_DF = pd.DataFrame({"predict":pred_restore.reshape(pred_restore.shape[0]), "label":y_test.reshape(y_test.shape[0])})
predict_DF["gap"] = predict_DF["predict"] - predict_DF["label"]
predict_DF

# RMSE로 Accuracy를 확인해보자.
>>> print("Accuracy:", np.sqrt(np.mean((pred_restore - y_test)**2)))
Accuracy: 0.07094477537881977

• 이전에 비해 확실히 빠르게 최적화가 되었으나, 여전히 예측값은 원하는 수준에 미치지 못한다.
• 굉장히 단순한 패턴임에도 불구하고, 아직까지 약간 다르다.

  이 정도로 단순한 패턴이라면, 예측값과 실제값의 차이가 거의 없어야 하나, 아직까지 차이가 크다는 생각이 든다. 다음 포스트에서는 최종적으로 한 가지를 수정하고, 해당 코드를 최종적으로 정리해보도록 하자.

 지난 포스트에서 작성한 코드들을 간략히 정리해보고, 본격적으로 학습 및 결과 평가를 해보자.

학습 목표

• 분석가가 알고 있는 패턴$f(x) = x + 10$에 대한 데이터를 생성하고, 그 패턴을 찾아내는 모델을 만들어보자.
• Input은 Node 1개, Output도 Node 1개인 연속형 데이터를 생성한다.

1. 지난 코드 정리

# Import Module
import pandas as pd
import numpy as np
from tensorflow import keras
from tensorflow.keras.layers import Dense



# Dataset Setting
def f(x):
    return x + 10
    
# Data set 생성
np.random.seed(1234)   # 동일한 난수가 나오도록 Seed를 고정한다.
X_train = np.random.randint(0, 100, (100, 1))
X_test = np.random.randint(100, 200, (20, 1))

# Label 생성
y_train = f(X_train)
y_test = f(X_test)



# Model Setting
model = keras.Sequential()
model.add(Dense(16, activation='relu'))
model.add(Dense(1, activation='linear'))



# Compile: 학습 셋팅
opt = keras.optimizers.Adam(learning_rate=0.01)
model.compile(optimizer=opt, loss = 'mse')

2. 학습 시작

>>> model.fit(X_train, y_train, epochs = 100)

• model.fit(): model에 대해 학습을 시작한다.
• fit() 안에는 train dataset, train data label, validation dataset 등이 들어갈 수 있다.
• validation dataset은 성능 향상에 도움이 되나, 꼭 필요한 것은 아니다.
• epochs은 전체 train set을 몇 번 학습할 것인가를 의미한다.
• 해당 코드를 실행하면 다음과 같은 문자들이 출력된다.

Epoch 1/100
4/4 [==============================] - 0s 2ms/step - loss: 955.4686
Epoch 2/100
4/4 [==============================] - 0s 998us/step - loss: 342.0951
Epoch 3/100
4/4 [==============================] - 0s 2ms/step - loss: 51.7757
Epoch 4/100
4/4 [==============================] - 0s 1ms/step - loss: 43.6929
Epoch 5/100
4/4 [==============================] - 0s 2ms/step - loss: 95.3333
Epoch 6/100
4/4 [==============================] - 0s 2ms/step - loss: 76.1808
Epoch 7/100
4/4 [==============================] - 0s 1ms/step - loss: 29.2552
Epoch 8/100
4/4 [==============================] - 0s 2ms/step - loss: 21.1532

...

Epoch 94/100
4/4 [==============================] - 0s 2ms/step - loss: 4.9562
Epoch 95/100
4/4 [==============================] - 0s 1ms/step - loss: 5.3142
Epoch 96/100
4/4 [==============================] - 0s 996us/step - loss: 5.0884
Epoch 97/100
4/4 [==============================] - 0s 2ms/step - loss: 4.9754
Epoch 98/100
4/4 [==============================] - 0s 2ms/step - loss: 5.3013
Epoch 99/100
4/4 [==============================] - 0s 1ms/step - loss: 5.0656
Epoch 100/100
4/4 [==============================] - 0s 1ms/step - loss: 4.4677
<tensorflow.python.keras.callbacks.History at 0x12fe8f0f520>

• 위 내용을 history라고 하며, 따로 history를 지정하지 않아도 출력된다.
• loss는 손실 값을 의미하며, 해당 값이 최소화되는 위치를 찾는 것이 목적이다.
• 일반적으로 loss가 0에 근사 해지는 것을 목적으로 한다.
• 만약 loss가 0에서 지나치게 먼 값에서 수렴한다면, 모델에 들어간 인자들(HyperParameter)이 잘못 들어간 것일 가능성이 매우 높으므로, 모델을 수정하길 바란다.
• loss가 지금처럼 0에 가깝게 내려 가긴 했으나, 그 정도가 0에 미치지 못한 경우 단순하게 epoch를 늘려보자.

>>> model.fit(X_train, y_train, epochs = 500)

Epoch 1/500
4/4 [==============================] - 1s 2ms/step - loss: 9528.2801
Epoch 2/500
4/4 [==============================] - 0s 2ms/step - loss: 7191.2032
Epoch 3/500
4/4 [==============================] - 0s 2ms/step - loss: 4662.3104
Epoch 4/500
4/4 [==============================] - 0s 1ms/step - loss: 2927.8638
Epoch 5/500
4/4 [==============================] - 0s 2ms/step - loss: 1738.3485
Epoch 6/500
4/4 [==============================] - 0s 2ms/step - loss: 877.1409

...

Epoch 495/500
4/4 [==============================] - 0s 2ms/step - loss: 0.0126
Epoch 496/500
4/4 [==============================] - 0s 1ms/step - loss: 0.0139
Epoch 497/500
4/4 [==============================] - 0s 1ms/step - loss: 0.0183
Epoch 498/500
4/4 [==============================] - 0s 1ms/step - loss: 0.0180
Epoch 499/500
4/4 [==============================] - 0s 2ms/step - loss: 0.0168
Epoch 500/500
4/4 [==============================] - 0s 2ms/step - loss: 0.0229

• Epochs를 500까지 올렸으나, loss 값이 원하는 만큼 나오지 않는 것을 볼 수 있다.

3. 결과를 확인해보자.

• 결과 확인은 상당히 단순하면서도 새로운 알고리즘을 만들어내야 할 필요성이 있는 영역이다.

>>>  model.predict(X_test.reshape(X_test.shape[0]))

array([[195.04504 ],
       [151.02899 ],
       [111.01437 ],
       [124.019135],
       [113.015114],
       [140.02496 ],
       [122.0184  ],
       [183.04066 ],
       [129.02095 ],
       [136.02351 ],
       [206.04909 ],
       [178.03883 ],
       [174.03737 ],
       [132.02205 ],
       [166.03447 ],
       [194.0447  ],
       [118.01694 ],
       [154.03008 ],
       [134.02278 ],
       [204.04832 ]], dtype=float32)

• model.predict(array): 들어간 array에 대하여 모델의 파라미터(가중치)들이 순방향으로 연산되어 나온 결과가 출력된다.
• 모델에 Input되는 데이터와 predict에 들어가는 데이터의 모양은 조금 다르다.

# 모델 Input 시
>>> X_test.shape
(20, 1)

# Predict Input 시
>>> X_test.reshape(X_test.shape[0]).shape
(20,)

• 모델 학습 시엔 데이터를 행 단위로 떨어뜨려 넣었다면, predict에선 위와 같이 넣어줘야 한다.

test set의 Label과 비교해보자.

• predict 결과와 Label 데이터인 y_test를 비교해보자.

pred = model.predict(X_test.reshape(X_test.shape[0]))
predict_DF = pd.DataFrame({"predict":pred.reshape(pred.shape[0]), "label":y_test.reshape(y_test.shape[0])})
predict_DF["gap"] = predict_DF["predict"] - predict_DF["label"]
predict_DF

• predict와 label이 어느 정도 근사하게 나오긴 하였으나, 얼마나 근사하게 나왔는지 보기가 어렵다.
• 모델을 평가하기 쉽도록, RMSE를 사용하여 Scalar값(숫자 1개)으로 바꿔주자.

>>> print("Accuracy:", np.sqrt(np.mean((pred - y_test)**2)))
Accuracy: 0.10477323661232778

• 0.1047로 나름 나쁘지 않은 결과가 나오긴 하였으나, $f(x) = x + 10$ 같이 굉장히 단순한 패턴을 만족스러운 수준으로 찾아내지 못했다.
• 게다가 패턴도 지나치게 단순한데, epochs가 500이나 사용되어, 생각보다 많은 자원이 낭비되었다.

 이번 포스트에서는 널리 알려진 방식대로 학습을 시켜보았다. 그러나, 아주 단순한 패턴임에도 불구하고, 쉽게 찾아내질 못하였으며, 그 결과도 원하는 것에 미치지 못했다.

 다음 포스트에서는 어디가 잘못되었는지 찾아내 이를 수정해보도록 하자.

 지난 포스트에서 데이터 셋에 대해 간략히 설명해보았다. 이번 포스트부터 본격적으로 텐서플로우를 사용해서, 내가 찾아내고 싶은 알고리즘을 찾아내 보자.

학습 목표

• 분석가가 알고 있는 패턴으로 데이터를 생성하고, 그 패턴을 찾아내는 모델을 만들어보자.
• Input이 1개, Output이 1개인 연속형 데이터에서 패턴을 찾아보자.

1. 데이터 셋 생성

• 패턴: $f(x) = x + 10$

# Module 설정
import pandas as pd
import numpy as np
from tensorflow import keras
from tensorflow.keras.layers import Dense

def f(x):
    return x + 10
    
# Data set 생성
np.random.seed(1234)   # 동일한 난수가 나오도록 Seed를 고정한다.
X_train = np.random.randint(0, 100, (100, 1))
X_test = np.random.randint(100, 200, (20, 1))

# Label 생성
y_train = f(X_train)
y_test = f(X_test)

데이터 셋 생성 코드의 함수 설명

1. np.random.seed(int):  난수(랜덤 한 데이터) 생성 시, 그 값은 생성할 때마다 바뀌게 된다. 데이터 셋이 바뀌게 되면, 일관된 결과를 얻기가 힘들어, 제대로 된 비교가 힘들어지므로, 난수를 생성하는 방식을 고정시킨다. 이를 시드 결정(Set seed)이라 하며, 숫자는 아무 숫자나 넣어도 상관없다.
2. np.random.randint(시작 int, 끝 int, shape): 시작 숫자(포함)부터 끝 숫자(미포함)까지 shape의 형태대로 array를 생성한다.

데이터 셋 생성 코드 설명

1. Train set은 0~100까지의 숫자를 랜덤으로 (100, 1)의 형태로 추출하였다.
2. Test set은 100~200까지의 숫자로 랜덤으로 (20, 1)의 형태로 추출했다. 여기서 값은 Train set과 절대 겹쳐선 안된다.
3. Label 데이터인 y_train과 y_test는 위에서 설정된 함수 f(x)에 의해 결정되었다.

• train 데이터 생김새(가시성을 위해 10개까지만 출력)

# train Dataset을 10개까지만 가져와보자
>>> X_train[:10]

array([[47],
       [83],
       [38],
       [53],
       [76],
       [24],
       [15],
       [49],
       [23],
       [26]])
       
>>> X_train.shape
(100, 1)

• 생성된 데이터 셋의 형태는 "(데이터 셋 수, 변수의 수)"라고 인지해도 좋다.
• 여기서 "변수의 수"는 "데이터 하나의 벡터 크기"라고 생각하는 것이 더 적합하다.
• 기본적으로 Tensorflow에 Input 되고 Output 되는 데이터의 형태는 이렇다고 생각하자.

2. 모델 생성하기

• tensorflow를 사용해 모델을 생성하는 경우, tensorflow가 아닌 keras를 사용하게 된다.
• 위에서 tensorflow의 기능을 가져올 때, 아래와 같은 코드로 가져왔다.
• from tensorflow import keras
• 이는, tensorflow라는 프레임워크에서 keras라는 모듈을 가지고 온다는 의미이다.
• keras는 추후 설명하게 될지도 모르지만, 모델 생성 및 학습에 있어 직관적으로 코드를 짤 수 있게 해 주므로, 쉽게 tensorflow를 사용할 수 있게 해 준다.
• 물론, keras와 tensorflow는 태생적으로 서로 다른 프레임워크이므로, 이 둘이 따로 에러를 일으켜, 에러 해결을 어렵게 한다는 단점이 있긴 하지만, 그걸 감안하고 쓸만한 가치가 있다.

model = keras.Sequential()
model.add(Dense(16, activation='relu'))
model.add(Dense(1, activation='linear'))

• keras를 사용해서 모델을 만드는 방법은 크게 2가지가 있다.
• 하나는 위 같이 add를 이용해서 layer를 하나씩 추가해 가는 방법이 있고

model = keras.Sequential([
    Dense(16, activation='relu'),
    Dense(1, activation='linear')
])

• 이렇게 keras.Sequential([]) 안에 층(layer)을 직접 넣는 방법이 있다.
• 처음 방법처럼 add를 사용하는 방법은 API 사용 방법이고, 아래와 같이 층을 Sequential([])에 직접 넣는 방식은 Layer 인스턴스를 생성자에게 넘겨주는 방법이라 하는데, 전자인 API를 사용하는 방법을 개인적으로 추천한다.
• 그 이유는 다중-아웃풋 모델, 비순환 유향 그래프, 레이어 공유 모델 같이 복잡한 모델 정의 시, 매우 유리하기 때문으로, 이는 나중에 다루겠으나, 이 것이 Tensorflow의 장점이다.

모델 생성 코드 함수 설명

1. keras.Sequential(): 순차 모델이라 하며, 레이어를 선형으로 연결해 구성한다. 일반적으로 사용하는 모델로 하나의 텐서가 입력되고 출력되는 단일 입력, 단일 출력에 사용된다. 다중 입력, 다중 출력을 하는 경우나, 레이어를 공유하는 등의 경우엔 사용하지 않는다.
2. model.add(layer): layer를 model에 층으로 쌓는다. 즉, 위 모델은 2개의 층을 가진 모델이다.
3. Dense(노드 수, 활성화 함수): 완전 연결 계층으로, 전, 후 층을 완전히 연결해주는 Layer다. 가장 일반적으로 사용되는 Layer다.

모델 생성 코드 설명

1. 해당 모델은 Input 되는 tensor도 1개 Output 되는 tensor도 1개이므로, Sequential()로 모델을 구성했다.
2. 은닉층에는 일반적으로 ReLU 활성화 함수가 사용된다고 하니, ReLU를 넣었다.
3. 출력층에는 출력 결과가 입력 값과 같은 노드 1개이므로, 노드 1개로 출력층을 만들었다. 
4. 일반적으로 Node의 수를 $2^n$으로 해야 한다고 하지만, 크게 상관없다는 말이 있으므로, 굳이 신경 쓰지 않아도 된다. 처음엔 자기가 넣고 싶은 값을 넣다가, 성능이 안 나온다 싶으면 바꿔보는 수준이니 크게 신경 쓰지 말자.
5. 사용된 활성화 함수(activation)는 일반적으로 은닉층에 ReLU를 넣고, 연속형 데이터이므로 출력층에 Linear를 넣어보았다.

• 해당 활성화 함수에 대해 궁금증이 들면, 다음 포스트(계단함수와 선형함수, 렐루 함수)를 확인하길 바란다.

3. 모델 컴파일하기

• 컴파일은 모델을 학습시키기 전에 어떤 방식으로 학습을 시킬지를 설정하는 과정이다.

opt = keras.optimizers.Adam(learning_rate=0.01)
model.compile(optimizer=opt, loss = 'mse')

코드 설명

1. keras.optimizers.Adam(): 최적화에 사용할 함수를 위처럼 외부에서 만들어서 넣는 경우, 학습률, 모멘텀 같은 인자들을 입맛에 맞게 바꿀 수 있다.
2. model.complie(): 학습 방식을 설정한다.

compile은 기본적으로 3가지 인자를 입력으로 받는다.

1. optimizer: 최적화하는 방법으로, 경사 하강법(GD)을 어떤 방법을 통해 사용할지를 결정한다. 일반적으로 Adam이 많이 사용된다.
2. loss: 손실 함수를 설정한다. 일반적으로 연속형 데이터라면 제곱 오차 시리즈를, 분류 데이터라면 교차 엔트로피 오차 시리즈를 사용한다.
3. metric: 기준이 되는 것으로, 분류를 할 때 주로 사용한다.

• 손실 함수와 최적화에 관심이 있다면 다음 포스트(손실 함수, 최적화)를 참고하길 바란다.

 자, 지금까지 학습을 위한 모델 세팅을 완료하였다. 다음 포스트에서는 위 코드들을 깔끔하게 정리하고, 실제 학습을 해보겠다.

 Tensorflow를 사용하는 사람 중 상당 수가 Github에서 다른 사람들이 어떤 목적을 위해 만들어놓은 모델을 그저 가져오거나, 남이 만든 모델에서 노드 크기를 수정하거나, 상황에 맞게 레이어를 바꿔보고, 내가 인공지능을 사용할 수 있다고 생각하는 경우가 많다.

 마치 통계 분석을 할 때, "서로 다른 두 집단이 있고, 그 집단에 대한 평균을 비교해보고 싶다면, t-test를 사용해야한다."라 생각하듯, 머신러닝에 접근하면, 인공지능을 단순한 마법의 상자로 생각해버릴 수 있다.

 흔히들 인공지능을 "내가 무언가를 넣으면, 원리는 잘 모르겠지만, 정답이 나오는 마법의 상자"라고 생각하는 경향이 있는데, 인공지능은 단순한 블랙박스가 아닌, 사용자가 의도를 가지고 설계한 것에 맞는 결과를 도출해주는 알고리즘이다.

 그러므로, 제대로 인공지능을 다루고자 한다면, 인공지능이 할 수 있는 영역 안에서 내가 원하는 결과를 이끌어낼 수 있어야 한다.

1. 데이터셋 생성하기

• 분석가라면, 상황에 맞는 실험용 데이터 셋 만들기는 기본 중 기본이다.
• 데이터셋은 크게 훈련(Train), 시험(Tes), 검증(Validation) 데이터 셋으로 나뉜다.

훈련 데이터 셋(Train Dataset)

• 신경망 훈련 시 사용되는, 모델 학습 용 데이터 셋으로, 수능을 보기 위해 공부하는 문제집에 해당한다.
• 과도하게 훈련 데이터셋을 학습시키는 경우, 과적합(Overfitting) 현상이 발생하여, 훈련 데이터 셋은 잘 분류하나, 시험 데이터 셋이나 실제 데이터에는 적합하지 않을 수 있다.
• 훈련 데이터 셋은 모델의 기준이 된다!

시험 데이터 셋(Test Dataset)

• 모델의 성능을 최종적으로 평가하기 위한 데이터 셋으로 실제 데이터 셋이다. 고등학교의 최종 목적 시험인 수능에 해당한다.
• 훈련 데이터 셋과 시험 데이터 셋은 중첩되지 않는 것이 좋다.
• 예를 들어, 데이터를 날짜별로 뽑아낼 수 있다면, 시험 데이터 셋은 다른 날짜의 데이터 셋을 사용하는 것이 좋다.
• 시험 데이터 셋과 모델이 예측한 결과를 비교해 정확도(Accuarcy), 정밀도(Precision), 재현율(Recall), F1 점수를 계산하여, 모델이 얼마나 잘 만들어졌는지를 확인해볼 수 있다.

검증 데이터 셋(Validation Dataset)

• 학습을 할 때, 학습이 얼마나 잘 돼는지를 평가하는 수단으로, 공부가 잘되었는지를 평가하는 모의고사에 해당 한다.
• Development Dataset이라고도 불린다.
• 검증 데이터 셋은 학습 시, 학습된 모델의 성능 평가에 사용되며, 그 결과가 파라미터에 반영된다.
• 즉, 검증 데이터 셋의 목적은 학습 데이터에 의해 학습된 파라미터 중, 실제 데이터에도 잘 맞을 수 있도록 최적의 파라미터를 찾아낼 수 있도록, 파라미터를 튜닝하기 위해 존재한다고 할 수 있다.
• 검증 데이더 셋은 학습 데이터 셋에서 분리되며, 때에 따라 검증 데이터 셋을 만들지 않고, 전부 훈련 데이터에 사용할 수도 있다.
• 물론, 검증 데이터 셋을 사용하는 경우 성능이 더 좋다고 한다.
• 학습 데이터 셋과 검증 데이터 셋은 그 내용이 중첩되지 말아야 한다. 만약 중첩되는 경우, 이 현상을 leakage라고 한다(학습 데이터 셋과 검증 데이터셋에 교집합 존재).

2. 과대 적합 피하기

• 모델이 훈련(Train) 데이터 셋에 대해선 분류가 잘되었으나, 시험(Test) 데이터 셋에 대해 구분을 지나치게 못한다면, 과대 적합일 가능성이 있다.
• 이는, 훈련 데이터 셋에 모델이 지나치게 맞춰져, 새로운 데이터에 대해 일반화가 되지 못한다는 소리로, 모델이 지나치게 훈련 데이터 셋에만 맞춰진, 모델의 분산이 큰 상태라고 할 수 있다.
• 이를 해결하는 방법은 다음과 같다.

1. 훈련 데이터를 늘린다.
2. Dropout과 같은 규제를 실시하여 복잡도를 줄인다.
3. 데이터의 차원을 줄인다.
4. 모델을 보다 간략화시켜 파라미터의 수를 줄인다.

• 위 내용은 꽤 심도 깊은 영역이므로, 이는 추후 자세히 다루도록 하겠다.

3. 데이터 셋의 비율

• 일반적으로 훈련(Train) 데이터셋과 시험(Test) 데이터셋의 비율은 7:3으로 나누며, 훈련 데이터의 안에서도 학습 도중 모델을 평가할 검증(Validation) 셋을 학습 데이터 셋에서 떼어내기도 한다. 이 경우, 일반적으로 훈련 데이터셋과 검증 데이터셋의 비율을 8:2로 한다고 한다.

• 그러나, 위 비율은 절대로 절대적인 것이 아니며, 총데이터의 양과 훈련 데이터 셋과 시험 데이터 셋의 형태 차이 등에 따라 그 비율은 위와 크게 다를 수 있다.
• 학습 데이터는 내가 원하는 특징이 잘 들어가 있는 깔끔한 데이터일 수 있으나, 실제 이 모델을 이용해 분류될 대상인 시험 데이터 셋엔 상당한 노이즈가 들어가 있을 수 있다.
• 예를 들어, 우리가 학습에 사용한 데이터는 증명사진이지만, 실제 사람들이 이 인공지능에 사용할 사진은 온갖 바탕과 포토샵 등 우리가 학습 시 고려하지 않은 노이즈가 들어가 있을 수 있다.
• 이를 방지하기 위해, 때에 따라 시험 데이터 셋이 없이 모두 학습 데이터로 사용하거나, 학습 데이터에 의도적으로 노이즈를 부여하기도 한다.
• 데이터 셋의 양이 매우 적다면(예를 들어, 데이터의 수가 1만에도 못 미친다면), 위 비율대로 나눠도 상관없으나, 데이터의 양이 매우 많다면(데이터의 수가 100만 이상이라면), 테스트 데이터 셋이나 검증 데이터 셋의 비율을 0.1~1%로 잡기도 한다.
• 즉, Valid Dataset과 Test Datset의 목적은 생소한 데이터를 이용해 모델을 일반화시키기 위한 것이므로, 그 비중이 그리 크지 않아도 된다(물론 Test Dataset은 최종 평가지만, 간접적으로 영향을 미치므로).

 다음 포스트에서는 실제로 데이터 셋을 생성하고, 이를 이용해서 학습을 해보고, 그 성능을 평가해보자!